1. 前言

栈和队列相关的题目是校招中出现频率一般，但是是属于相对基础的题型。我们要关注两类问题，栈和队列的添加和删除操作，以及栈和队列之间的区别和联系。

2. 栈和队列

2.1 数据结构

首先我们给出栈和队列的数据结构定义：

（1）栈（Stack）：允许在某一端插入元素（即push操作），以及删除元素（即pop操作）的数据结构，必须满足后进先出（LIFO：Last In First Out）的运算规则。
一个典型的栈数据结构如下图所示：

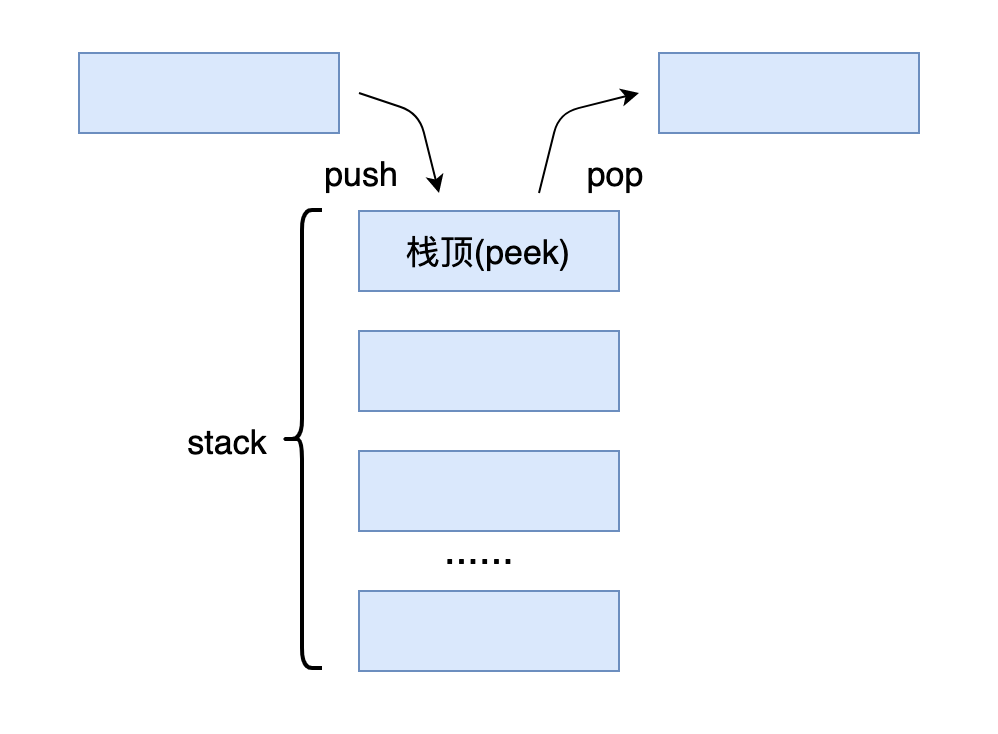
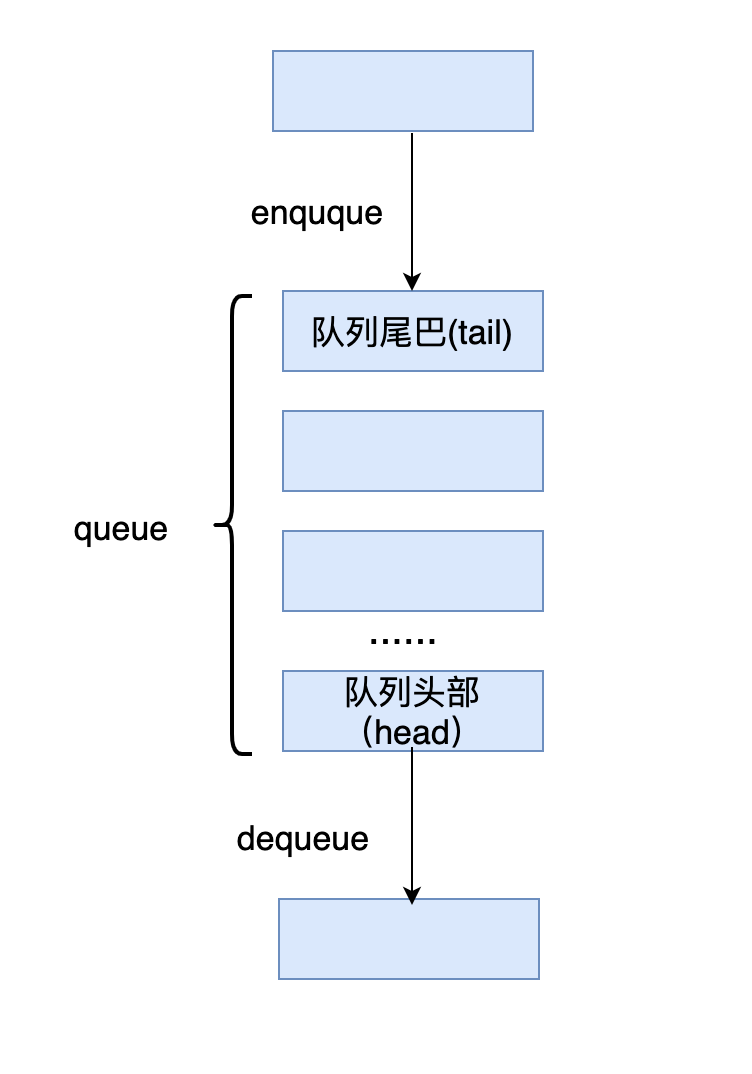
（2）队列（Queue）：允许在某一端插入元素（即enqueue操作），以及在另一端删除元素（即dequeue操作）的数据结构，必须满足先进先出（FIFO：First In First Out）的运算规则。
一个典型的队列数据结构如下图所示：

2.2 用两个栈实现一个队列

面试官提问：能否用两个栈实现一个队列的数据结构？

题目解析：

反转链表是来源于算法网站LeetCode的经典题目，题目链接：https://leetcode-cn.com/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof/。

本题是一道非常经典的面试题，我们不能直接使用语言自带的Queue实现类，需要手动用两个栈来模拟队列的操作。

在解题之前，我们需要对栈和队列有个前置理解，栈支持入栈和出栈操作，队列支持入队和出队操作。并且从题目看，队列还需要实现peek函数（返回队列的头部元素）和empty函数（判断队列是否为空）。举例来说，我们假设实现的队列类名是MockQueue，基础的操作案例示例：

MockQueue queue = new MockQueue();
queue.push(100);  //将100放入队列
queue.push(200);  //将200放入队列
queue.empty();    //判断队列是否为空，return false
queue.pop();      //弹出队列的一个元素
queue.peek();     //返回队列的头部元素，return 100

我们用 stack1、stack2 来表示两个栈，还是以小规模数据作为案例开始分析，对于一个数组[1,2,3,4]，我们将其存放到第一个栈stack1中，那么出栈的顺序是[4,3,2,1]，明显不满足队列的要求。入栈和出栈的操作是将数组逆序排列了一遍，从几何的角度可以看成旋转了180度，如果连续两次旋转180度，那么数组就会回到原点，分析到这里解法就呼之欲出了。

从分工上看，stack1 负责 push，stack2 负责 pop。

（1）入队的操作：我们直接把值放到 stack1；
（2）出队的操作：首先判断 stack2 是否为空，如果为空就把 stack1 中的元素全部压入 stack2，最后弹出 stack2 的栈顶元素；
（3）返回队列头部元素的操作：peek 操作和 pop 操作类似，区别在于不会弹出 stack2 的栈顶元素；
（4）判断队列是否为空的操作：直接判断 stack1 和 stack2 是否同时为空就行。

下面给出Java源码的实现，示例：

class MockQueue {
    //首先我们需要定义两个Stack数据结构
    Stack<Integer> s1;
    Stack<Integer> s2;

    public MockQueue() {
        // 初始化对象
        s1 = new Stack<>();
        s2 = new Stack<>();
    }
    
    public void push(int x) {
        //入队操作
        s1.push(x);
    }
    
    public int pop() {
        //出队操作
        if(s2.isEmpty()){
            while(!s1.isEmpty()){
                s2.push(s1.pop());
            }
        }
        return s2.pop();
    }
    
    public int peek() {
        //从队列头部获取元素
        if(s2.isEmpty()){
            while(!s1.isEmpty()){
                s2.push(s1.pop());
            }
        }
        return s2.peek();
    }
    
    public boolean empty() {
        //判断队列是否为空
        return s1.isEmpty() && s2.isEmpty();
    }
}

3. 小结

本章节我们介绍了最基础的数据结构，栈和队列，其中栈在动态规划以及二叉树问题中也经常出现。在使用栈和队列解决算法问题时，需要特别注意容器为空的情况，防止抛出异常。这类边界问题的判断，在其他算法问题中也是注意点，例如二叉树首先要判断 root 是否为空，防止空指针访问异常。