-
看不懂怎么回事……查看全部
-
线性回归算法
矩阵算法、梯度算法
 查看全部
查看全部 -
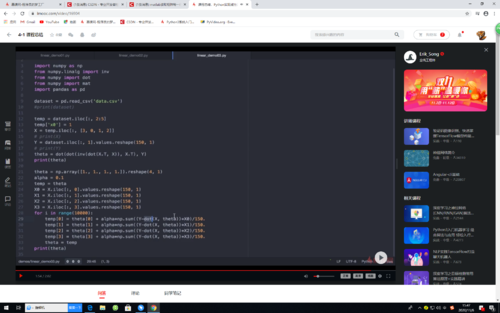
梯度下降法计算
 查看全部
查看全部 -
矩阵的操作
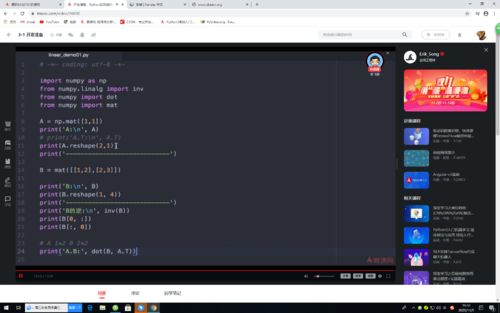 查看全部
查看全部 -
矩阵A,B的点成:np.dot(A,B)
查看全部 -
矩阵B的逆:np.inv(B)
查看全部 -
矩阵A的转置:A.T
查看全部 -
最小二乘法模型
查看全部 -
梯度下降函数
查看全部 -
直接运算的问题
矩阵需要满秩
运算性能
查看全部 -
最小二乘法模型
查看全部 -
线性回归的数学表示
查看全部 -
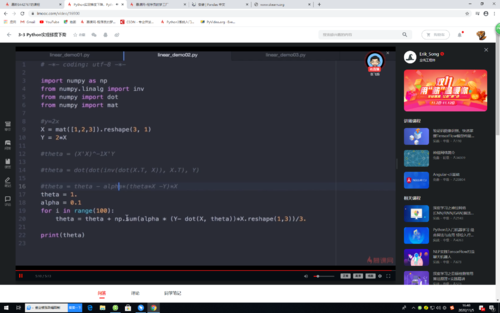
θ=theta
alpha是学习速率[0,1]——
//保证梯度下降的速率不要太快,在一个合适的区间之内,是函数迅速收敛,找到局部最小值
theta=theta-alpha(theta * X - Y)*X
np.sum()/组数——加权平均
import numpy as np from numpy.linalg import inv from numpy import dot from numpy import mat if __name__ == "__main__": # 训练数据 x = mat([1, 2, 3]).reshape(3, 1) # 1行3列转化为3行1列 y = 2 * x #梯度下降: # 原理:多次更新theta的值,通过theta与x,y的关系来得到theta # theta = theta - alpha*(theta*x-y)*x (alpha取值为0到1,保证梯度下降的变化速率不要太快,在一个合适的区间之内,使得函数迅速收敛,找到局部最小值) theta = 1.0 #初始化theta alpha = 0.1 #初始化alpha for i in range(100): theta = theta + np.sum(alpha * (y - dot(x, theta)) * x.reshape(1, 3))/3 # np.sum 求加权平均值 print(theta)
查看全部 -
import numpy as np from numpy.linalg import inv from numpy import dot from numpy import mat if __name__ == "__main__": A = np.mat([1, 1]) # 1行2列的矩阵 print('A:\n', A) Arr = np.array([1,1]) #数组 print("Arr:\n",Arr) #A矩阵是1*2转化为2*1 print("A矩阵转化2行1列:", A.reshape(2, 1)) # A矩阵转置 print('A.T:\n', A.T) # 1行2列 转置为 2行1列 print("-------------------------") B = mat([[1,2],[2,3]]) #2*2的矩阵 print('B:\n',B) #求B矩阵的逆矩阵 print('B的逆矩阵:\n', inv(B)) #获取B矩阵的第一行 print("B矩阵的第一行",B[0, :]) #第一行所有列 #获取B矩阵的第一列 print("B矩阵的第一列:", B[:, 0]) #所有行第一列 print("B矩阵转化为1行4列:\n", B.reshape(1, 4)) # A: 1*2 B: 2*2 print('A*B:\n', dot(A,B)) # A.T 2*1 B:2*2 print('B*A:\n', dot(B,A.T)) #B矩阵*A的转置矩阵查看全部 -
梯度下降算法
查看全部 -
直接计算的问题
查看全部 -
最小二乘法模型
向量表示
Y=θX,θ和X是矩阵
L=1/2(θX-Y)^T(θX-Y)
第二行为损失函数(欧几里得距离/向量中向量空间的距离)
//这个损失函数是线性的,而神经网络的损失函数是非线性的
查看全部 -
线性回归的数据表示
查看全部 -
什么是线性回归
y~x :y与x是一对一的关系,映射到几何上就是二维坐标系中的直线方程
Y = θX
通过训练,得到θ的过程,就是线性回归算法。
其中:x是输入,y是输出,是结果
查看全部
举报
0/150
提交
取消







