-
掌握python梯度下降求解线性分析模型参数
θ=theta
alpha是学习速率[0,1]——
//保证梯度下降的速率不要太快,在一个合适的区间之内,是函数迅速收敛,找到局部最小值
theta=theta-alpha(theta * X - Y)*X
np.sum()/组数——加权平均
>>> import numpy as np
>>> from numpy.linalg import inv
>>> from numpy import dot
>>> from numpy import mat
>>> X=mat([1,2,3]).reshape(3,1)
>>> Y=2*X
>>> theta=1.0
>>> alpha=0.1
>>> for i in range(100):
... theta=theta + np.sum(alpha*(Y-dot(X,theta))*X.reshape(1,3))/3.0
...
>>> print(theta)
2.0
>>>
查看全部 -
本次不要截距,用一个过原点的方程来作为例子
y=2x
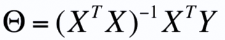
θ=(X^T X)^-1 * X^T Y
>>> import numpy as np
>>> from numpy.linalg import inv
>>> from numpy import dot
>>> from numpy import mat
>>> X=mat([1,2,3]).reshape(3,1)
>>> Y=2*X
>>> theta=dot(dot(inv(dot(X.T,X)),X.T),Y)
>>> print(theta)
[[2.]]
>>>
查看全部 -
A.reshape(1,2)
把A输出成1行2列的形式
查看全部 -
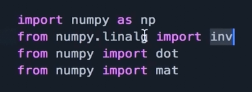
inv是求矩阵的逆
dot是矩阵点乘dot(A,B)
mat是矩阵是二维的
Array数组维度是一维的
".T" 矩阵的转置
查看全部 -
理解通过梯度下降进行参数求解过程
直接计算的问题
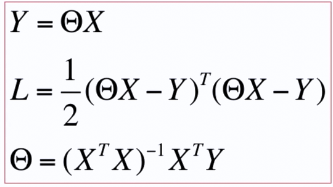
矩阵是否满秩(Python矩阵运算对于不是满秩矩阵的情况适用模糊近似处理)
运算性能
梯度下降法近似的计算,解决了直接计算的问题
查看全部 -
理解向量运算进行参数求解过程
向量表示
Y=θX,θ和X是矩阵

L=1/2(θX-Y)^T(θX-Y)
第二行为损失函数(欧几里得距离/向量中向量空间的距离)
//这个损失函数是线性的,而神经网络的损失函数是非线性的
目的是找到一个L,使函数最小
//求极值或者求最小值就是对一个函数求导
θ=((X^T)X)^-1(X^T)Y //参数计算
就是第二行的损失函数的求导结果
查看全部 -
线性回归的一般化模型的数学表示
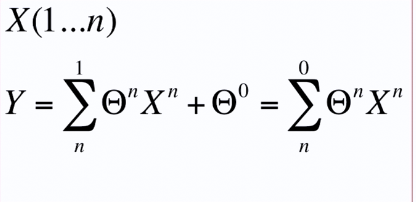
θ^0表示一维时的截距
也表示为多维时的偏移量
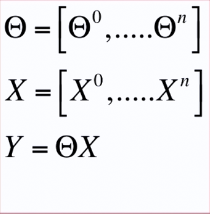 查看全部
查看全部 -
通过训练得到θ的过程称为线性回归
查看全部 -
线性回归是最简单的模型
查看全部 -
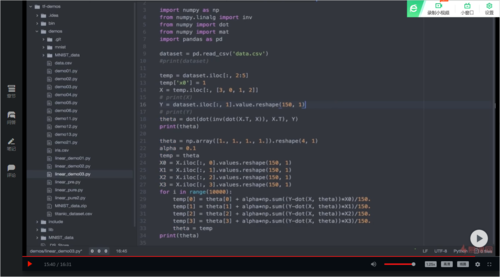
from numpy import * import pandas as pd dataset = pd.read_csv('data.csv') temp = dataset.iloc[:, 2:5] temp['x0'] = 1 X = temp.iloc[:, [3, 0, 1, 2]] Y = dataset.iloc[:, 1] #(X'X)^(-1)X'Y,随着训练集增大,计算速度变慢 theta = dot(dot(inv(dot(X.T, X)), X.T), Y) #梯度下降法:theta = theta - alpha*(theta*X - Y)*X theta = array([1., 1., 1., 1.]).reshape(4, 1) #初始化theta alpha = 0.1 #定义学习率,若不收敛-->调小,若效率慢-->调大 temp = theta #同步更新theta,需要temp缓存 X0 = X.iloc[:, 0].values.reshape(150, 1) X1 = X.iloc[:, 1].values.reshape(150, 1) X2 = X.iloc[:, 2].values.reshape(150, 1) X3 = X.iloc[:, 3].values.reshape(150, 1) for i in rage(10000): temp[0] = theta[0] - alpha*dot(X0.T, dot(X, theta)-Y) temp[1] = theta[1] - alpha*dot(X1.T, dot(X, theta)-Y) temp[2] = theta[2] - alpha*dot(X2.T, dot(X, theta)-Y) temp[3] = theta[3] - alpha*dot(X3.T, dot(X, theta)-Y) theta = temp查看全部 -
0,Y,X1,X2,X3 1,5.1,3.5,1.4,0.2 2,4.9,3.0,1.4,0.2 3,4.7,3.2,1.3,0.2 4,4.6,3.1,1.5,0.2 5,5.0,3.6,1.4,0.2 6,5.4,3.9,1.7,0.4 7,4.6,3.4,1.4,0.3 8,5.0,3.4,1.5,0.2 9,4.4,2.9,1.4,0.2 10,4.9,3.1,1.5,0.1 11,5.4,3.7,1.5,0.2 12,4.8,3.4,1.6,0.2 13,4.8,3.0,1.4,0.1 14,4.3,3.0,1.1,0.1 15,5.8,4.0,1.2,0.2 16,5.7,4.4,1.5,0.4 17,5.4,3.9,1.3,0.4 18,5.1,3.5,1.4,0.3 19,5.7,3.8,1.7,0.3 20,5.1,3.8,1.5,0.3 21,5.4,3.4,1.7,0.2 22,5.1,3.7,1.5,0.4 23,4.6,3.6,1.0,0.2 24,5.1,3.3,1.7,0.5 25,4.8,3.4,1.9,0.2 26,5.0,3.0,1.6,0.2 27,5.0,3.4,1.6,0.4 28,5.2,3.5,1.5,0.2 29,5.2,3.4,1.4,0.2 30,4.7,3.2,1.6,0.2 31,4.8,3.1,1.6,0.2 32,5.4,3.4,1.5,0.4 33,5.2,4.1,1.5,0.1 34,5.5,4.2,1.4,0.2 35,4.9,3.1,1.5,0.1 36,5.0,3.2,1.2,0.2 37,5.5,3.5,1.3,0.2 38,4.9,3.1,1.5,0.1 39,4.4,3.0,1.3,0.2 40,5.1,3.4,1.5,0.2 41,5.0,3.5,1.3,0.3 42,4.5,2.3,1.3,0.3 43,4.4,3.2,1.3,0.2 44,5.0,3.5,1.6,0.6 45,5.1,3.8,1.9,0.4 46,4.8,3.0,1.4,0.3 47,5.1,3.8,1.6,0.2 48,4.6,3.2,1.4,0.2 49,5.3,3.7,1.5,0.2 50,5.0,3.3,1.4,0.2 51,7.0,3.2,4.7,1.4 52,6.4,3.2,4.5,1.5 53,6.9,3.1,4.9,1.5 54,5.5,2.3,4.0,1.3 55,6.5,2.8,4.6,1.5 56,5.7,2.8,4.5,1.3 57,6.3,3.3,4.7,1.6 58,4.9,2.4,3.3,1.0 59,6.6,2.9,4.6,1.3 60,5.2,2.7,3.9,1.4 61,5.0,2.0,3.5,1.0 62,5.9,3.0,4.2,1.5 63,6.0,2.2,4.0,1.0 64,6.1,2.9,4.7,1.4 65,5.6,2.9,3.6,1.3 66,6.7,3.1,4.4,1.4 67,5.6,3.0,4.5,1.5 68,5.8,2.7,4.1,1.0 69,6.2,2.2,4.5,1.5 70,5.6,2.5,3.9,1.1 71,5.9,3.2,4.8,1.8 72,6.1,2.8,4.0,1.3 73,6.3,2.5,4.9,1.5 74,6.1,2.8,4.7,1.2 75,6.4,2.9,4.3,1.3 76,6.6,3.0,4.4,1.4 77,6.8,2.8,4.8,1.4 78,6.7,3.0,5.0,1.7 79,6.0,2.9,4.5,1.5 80,5.7,2.6,3.5,1.0 81,5.5,2.4,3.8,1.1 82,5.5,2.4,3.7,1.0 83,5.8,2.7,3.9,1.2 84,6.0,2.7,5.1,1.6 85,5.4,3.0,4.5,1.5 86,6.0,3.4,4.5,1.6 87,6.7,3.1,4.7,1.5 88,6.3,2.3,4.4,1.3 89,5.6,3.0,4.1,1.3 90,5.5,2.5,4.0,1.3 91,5.5,2.6,4.4,1.2 92,6.1,3.0,4.6,1.4 93,5.8,2.6,4.0,1.2 94,5.0,2.3,3.3,1.0 95,5.6,2.7,4.2,1.3 96,5.7,3.0,4.2,1.2 97,5.7,2.9,4.2,1.3 98,6.2,2.9,4.3,1.3 99,5.1,2.5,3.0,1.1 100,5.7,2.8,4.1,1.3 101,6.3,3.3,6.0,2.5 102,5.8,2.7,5.1,1.9 103,7.1,3.0,5.9,2.1 104,6.3,2.9,5.6,1.8 105,6.5,3.0,5.8,2.2 106,7.6,3.0,6.6,2.1 107,4.9,2.5,4.5,1.7 108,7.3,2.9,6.3,1.8 109,6.7,2.5,5.8,1.8 110,7.2,3.6,6.1,2.5 111,6.5,3.2,5.1,2.0 112,6.4,2.7,5.3,1.9 113,6.8,3.0,5.5,2.1 114,5.7,2.5,5.0,2.0 115,5.8,2.8,5.1,2.4 116,6.4,3.2,5.3,2.3 117,6.5,3.0,5.5,1.8 118,7.7,3.8,6.7,2.2 119,7.7,2.6,6.9,2.3 120,6.0,2.2,5.0,1.5 121,6.9,3.2,5.7,2.3 122,5.6,2.8,4.9,2.0 123,7.7,2.8,6.7,2.0 124,6.3,2.7,4.9,1.8 125,6.7,3.3,5.7,2.1 126,7.2,3.2,6.0,1.8 127,6.2,2.8,4.8,1.8 128,6.1,3.0,4.9,1.8 129,6.4,2.8,5.6,2.1 130,7.2,3.0,5.8,1.6 131,7.4,2.8,6.1,1.9 132,7.9,3.8,6.4,2.0 133,6.4,2.8,5.6,2.2 134,6.3,2.8,5.1,1.5 135,6.1,2.6,5.6,1.4 136,7.7,3.0,6.1,2.3 137,6.3,3.4,5.6,2.4 138,6.4,3.1,5.5,1.8 139,6.0,3.0,4.8,1.8 140,6.9,3.1,5.4,2.1 141,6.7,3.1,5.6,2.4 142,6.9,3.1,5.1,2.3 143,5.8,2.7,5.1,1.9 144,6.8,3.2,5.9,2.3 145,6.7,3.3,5.7,2.5 146,6.7,3.0,5.2,2.3 147,6.3,2.5,5.0,1.9 148,6.5,3.0,5.2,2.0 149,6.2,3.4,5.4,2.3 150,5.9,3.0,5.1,1.8
查看全部 -
总代码记录
 查看全部
查看全部 -
Python实现线性回归分析:
技术背景:机器学习的兴起 线性回归模型的特点
实际意义:金融 数学 医学 统计
查看全部 -
牛逼了,不明觉厉
查看全部 -
用梯度下降算法来实现:
1、梯度下降算法方程:theta = theta - alpha*(theta*X - Y)*X
2、程序实现:
alpha = 0.1
theta = 1.0
for i in range(100):
theta = theta + np.sum(alpha * (Y - dot(X, theta)) * X.reshape(1, 3))/3
查看全部
举报








