-
网络梯度下降
查看全部 -
全部训练损失
查看全部 -
三种激励函数:Sigmoid,tanh,ReLU
查看全部 -
神经网络包含
查看全部 -
逻辑回归模型
查看全部 -
神经元
线性组合
非线性处理
查看全部 -
网络结构
激励函数
损失函数
梯度下降
查看全部 -
用激励函数正向运算输入值得到损失,若损失过大,用梯度下降函数对W,b进行调整
重复正向运算,知道损失达到最小
查看全部 -
左边利用输入值通过每一层网络的结构计算出下一层输出
直到结束,计算出损失
右边通过损失函数不断更新W,b,知道计算出最小的损失函数
查看全部 -
观察神经网络过程形成较为直观的理解
梯度下降逆向更新W,b
一边正向一边逆向,重复这个流程
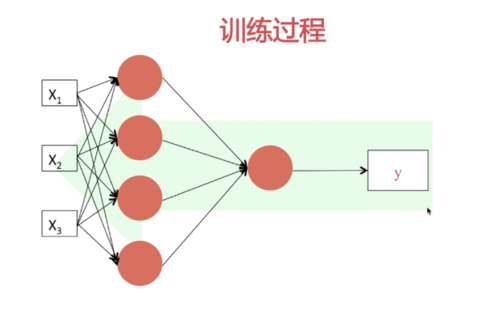
训练过程
左边成为正向传播
通过输入值按照每一层网络的结构计算出下一层的输出
直到结束,结束的时候计算出整个网络的损失
右侧是一个参数(W,b)调校的过程
通常会用到左边的W,b参数,而这些参数通常是会缓存的,这样会提高我们的运算效率(z^n,W^n,b^n)
实际上是逐步更新参数的过程
然后用新的参数载重复上面的过程
知道我们的损失函数趋向于一个最小值
参数全部算好然后一次性更新
查看全部 -
神经网络的梯度下降——反向传播
通过运算结果,逆向调节每一层的W,b,从而使整个神经链条达到一种最佳的状态
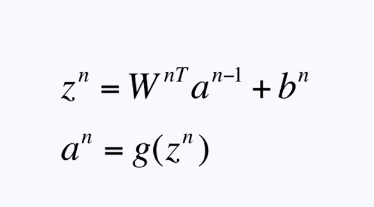
通过w,b的线性运算和激励函数的操作,在每一层上通过这两部得到下一层的输入值
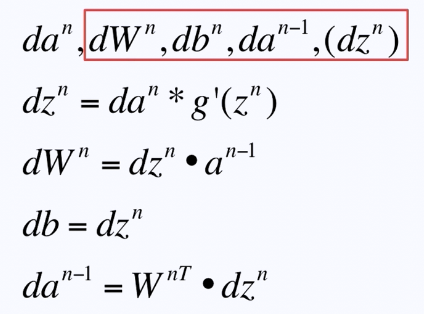
倒数第二层不需要调校
查看全部 -
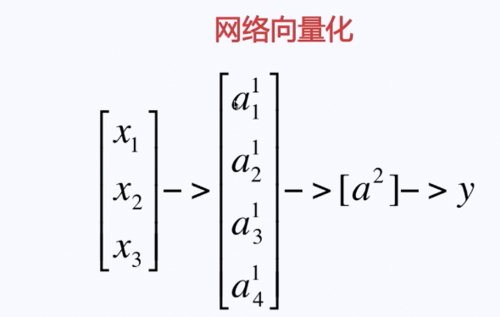
神经网络的网络向量化
神经网络的向前传播、运算、预测——神经网络的网络向量化,对向量化进行计算的过程

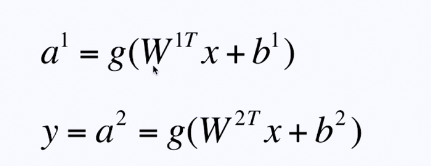
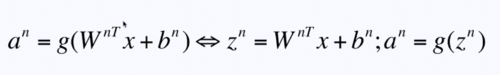 查看全部
查看全部 -
逻辑回归中的梯度下降
w和b决定函数的样子
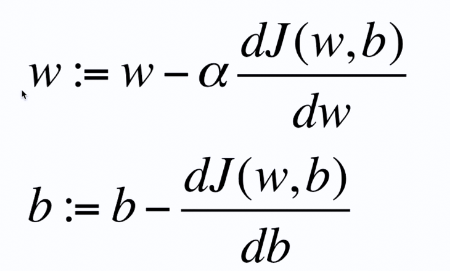
w和b同步更新
α是学习的速率,避免计算太快,错过合适的W,
w=w-a*(损失函数对w进行求导)
查看全部 -
单次训练损失
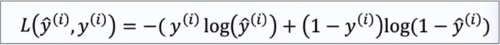
全部训练损失(就是把单次训练损失加起来)
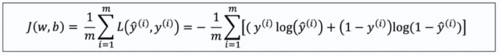 查看全部
查看全部 -
激励函数:
作用:提供规模化的非线性能力
包括:Sigmoid、tanh、ReLU等
Sigmoid函数适用于结果为判断是非的场合,但由于其对称中心在(0, 0.5),还需要进行数据中心化,由此提出了其改进函数tanh
Sigmiod和tanh的缺点是当数值很大或很小时,结果变化比较平缓,由此提出了ReLU函数,
而ReLU函数作为最普遍使用的激励函数,我们有时会使用斜率为负但是绝对值比正数小的线
查看全部
举报