-
条件概率
 查看全部
查看全部 -
 积分查看全部
积分查看全部 -
 梯度下降法查看全部
梯度下降法查看全部 -
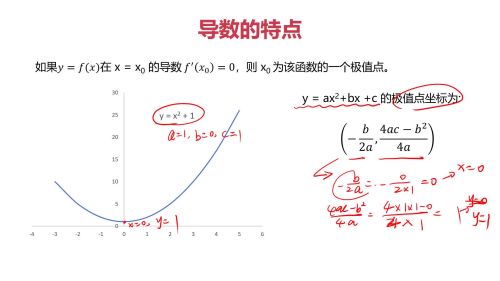
极值点计算
查看全部 -
导数公式
 查看全部
查看全部 -
非线性函数导数
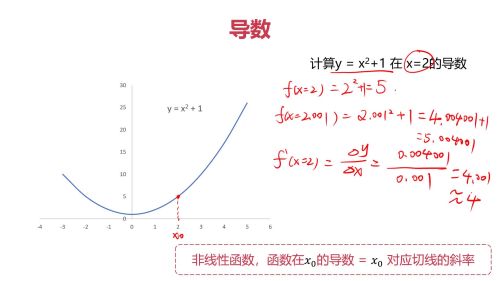 查看全部
查看全部 -
线性函数导数
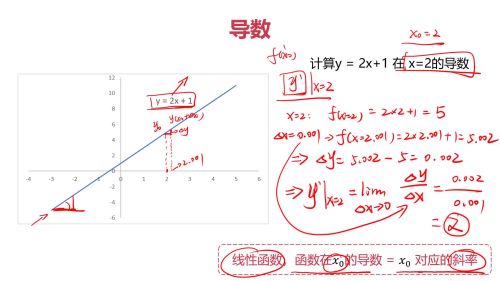 查看全部
查看全部 -
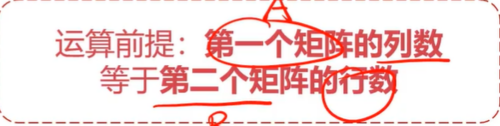
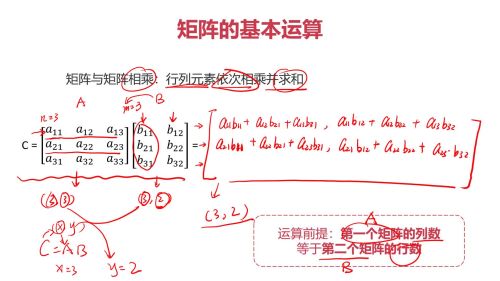 矩阵运算查看全部
矩阵运算查看全部 -
我的笔记
查看全部 -
我
 查看全部
查看全部 -


注意
查看全部 -
**平方符号
diff( )求导函数
integrate( , )求积分函数
limit( , , )求极限函数
查看全部 -
Python实现函数微分积分
 查看全部
查看全部 -
不定积分:函数f的不定积分,是一个可导函数F且其导数等于原本的函数f,即F‘= f (函数的不定积分可以理解为其对应的反导数,有无穷多个)
定积分:对于一个给定的正实值函数f(x),在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值
通过积分求概率
概率密度:概率密度函数是一个描述随机变量在某个确定的取值点附近的可能性的函数
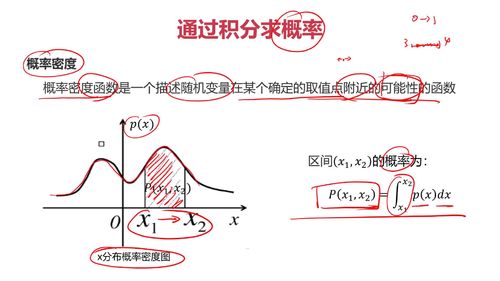
积分公式

查看全部 -
梯度下降法

梯度下降法举例
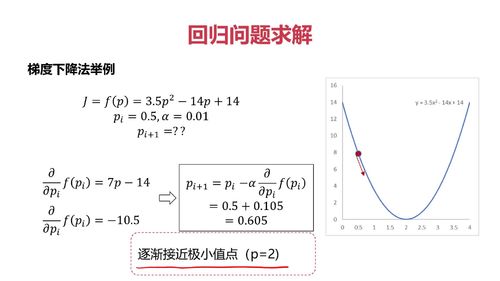
核心:从一个点出发,沿着导数的反方向逐步逼近极值点
回归问题求解
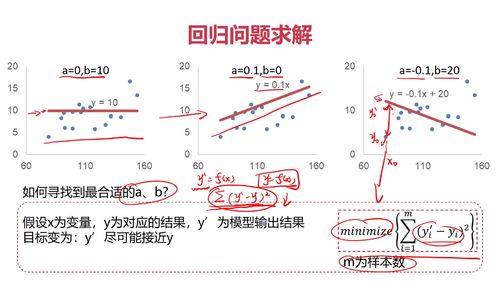
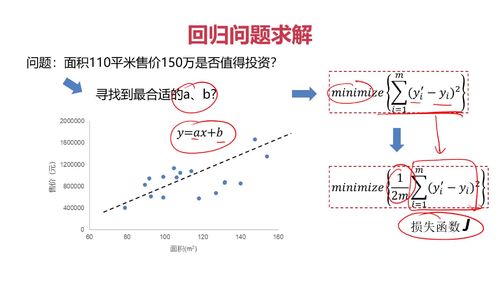

查看全部
举报
0/150
提交
取消






