-
实战问题:


代码(已验证):
# 导入pandas库, numpy库
import pandas as pd
import numpy as np
# 将数据预先储存为一个csv文件,然后加载到开发环境中来
# 读取数据
data = pd.read_csv("chapter3_data.csv")
# 查看数据
data.head()
# X赋值
# 将y的一列单独去掉,axis=0为行,axis=1为列
X = data.drop(["y"], axis=1)
print(X)
#y赋值
y = data.loc[:,"y"]
print(y)
#建立模型
# 从sklearn包的naive_bayes之中导入CategoricalNB
from sklearn.naive_bayes import CategoricalNB
# 建立模型实例
model = CategoricalNB()
# 训练模型
model.fit(X, y)
# 预测 测试集数据
# 预测y=1or=0的概率
y_predict_proba = model.predict_proba(X)
# 输出y的预测值
y_predict = model.predict(X)
#计算模型准确率
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y, y_predict)
print(accuracy)
# 任务二:
# 测试样品X_test的预测
# 先将其转化成为数组形式
X_test = np.array([[0,0,0,1,1,0]])
print(X_test)
# 预测样品的购买或不购买的概率
y_predict_proba = model.predict_proba(X_test)
print(y_predict_proba)
# 输出样品的预测值
y_test = model.predict(X_test)
print(y_test)
查看全部 -
贝叶斯公式:

贝叶斯公式延伸:(和全概率公式结合)

贝叶斯公式例子:

朴素贝叶斯:
y表示可能的分类,比如y1,y2,y3. 求P(y1),P(y3),P(y3),如果P(y1)最大,说明应该分类到y1.
第一个公式:X,表示一行,一条记录。P(Y|X)含义:在符合X的所有特征的情况下,yi 的概率。比如:使用iphone,男性,购买可能的概率。X是个向量,是一行。xj指的是本条记录(一个用户)的第j个特征。
第二个公式 P(xj | y = yi)的含义:x表示一行,一条记录。总的含义是,在y为yi的情况下,特征 x 取值为(x1..xj ...xm)(并的关系) 的概率。 例子:购买课程 的条件下(yi),使用ipone 而且为男性的 概率 = 购买课程的条件下(yi)使用iphone的概率 乘以 购买课程 的条件下(yi)为男性的概率 。
第三个公式,是展开了公式1。分子1: P(Y)好说,就是P(yi),购买课程的概率。分子2: 就是公式2。 分母就是P(X)的概率,例子:使用iphone且为男性的概率。分母P(X)等于P(x1)*P(x2)... 就是,等于 使用ipone的概率 乘以 男性的概率。PS:前提是 x1,x2 ... xm (m个特征),特征独立, 就是使用的手机型号和性别 两个因素独立。

朴素贝叶斯例子:
 查看全部
查看全部 -
全概率公式:(通过局部事件概率,计算在整个事件的概率)
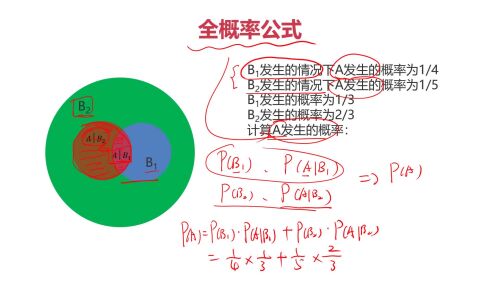
PS:P(B1) + P(B2)+... + P(Bn) 应该等于1吧
PS:全概率公式 有点类似 分治法。
 查看全部
查看全部 -
条件概率:

条件概率例子:
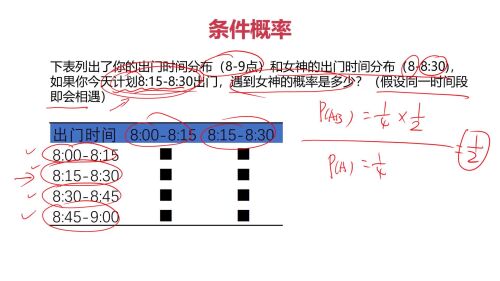 查看全部
查看全部 -
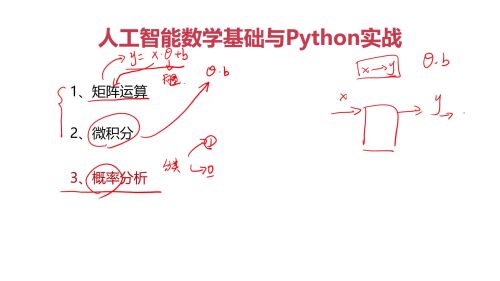
三者关系:
矩阵:可以用来“表示”,N个变量之间的关系。
微积分:求解关系中的参数。
概率:#1分类中,属于某一类的概率。应该还有其他作用,没提。
概率:
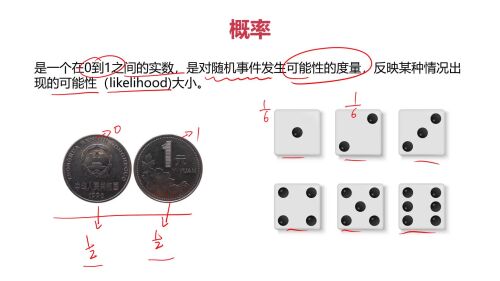
机器学习中的概率:

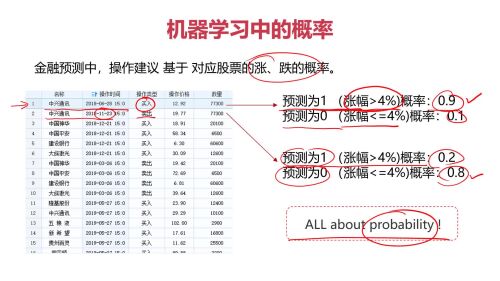 查看全部
查看全部 -
不定积分:

定积分:
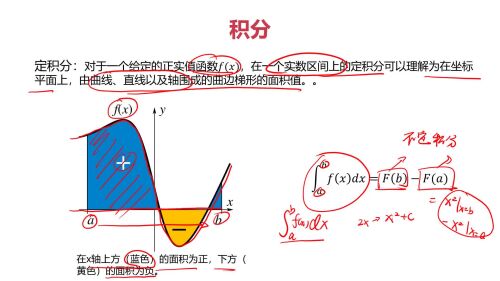
定积分求解:

定积分在机器学习中的意义:根据概率密度函数求概率
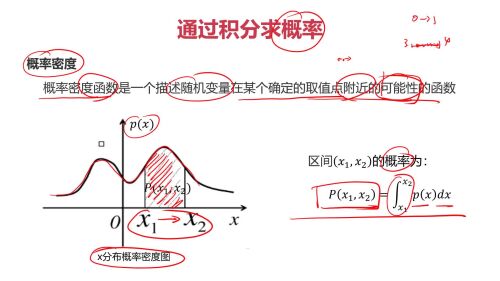
常用的积分公式:
 查看全部
查看全部 -
梯度下降法:

梯度下降举例:求极小值点
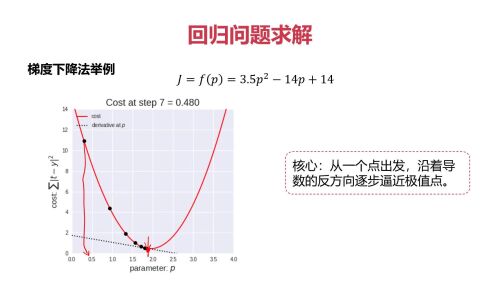
例子2:回归问题
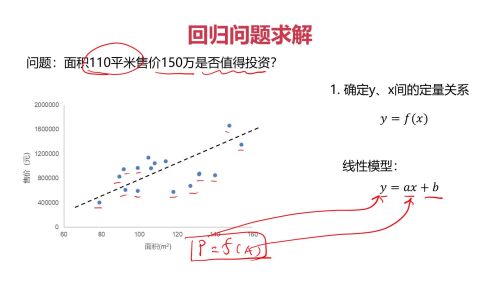
例子2:回归问题:如何找合适a,b?方差(损失函数)最小
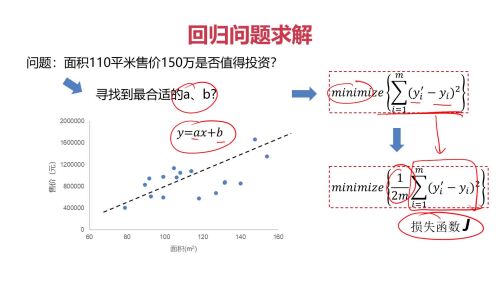
例子2:回归问题:如何找下一个点
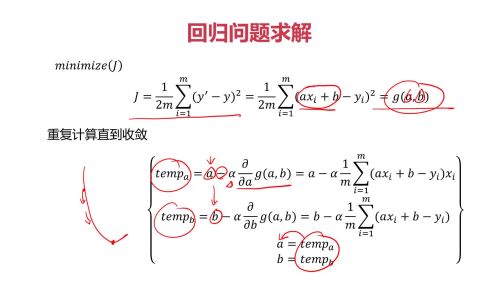
例子2:回归问题:求解效果
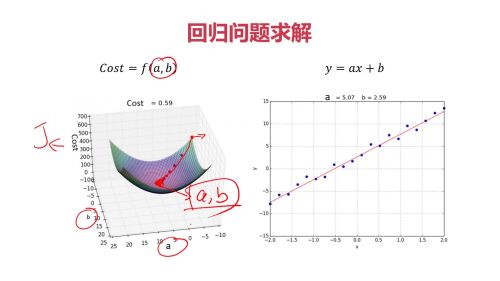 查看全部
查看全部 -
极限:
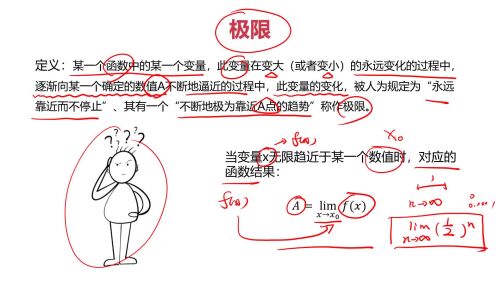
求极限:

导数:
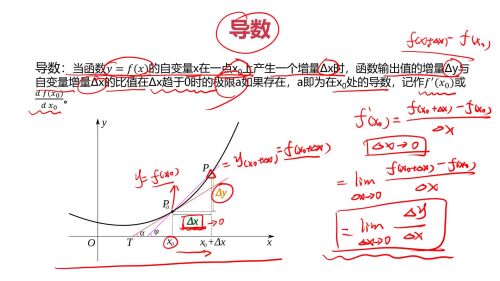
导数求解例子1:
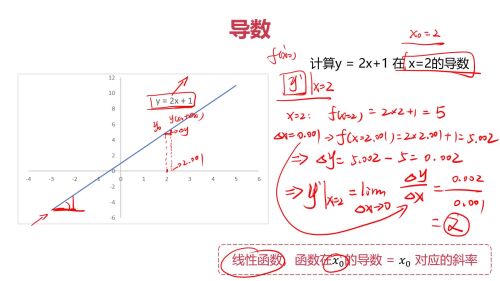
导数求解例子2:
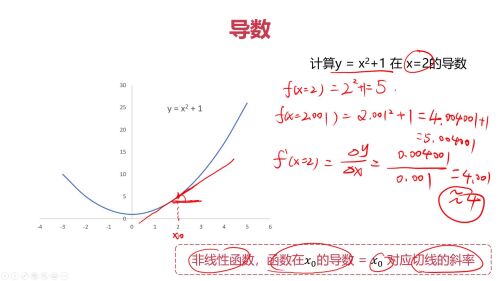
常用导数公式:

导数的特点:
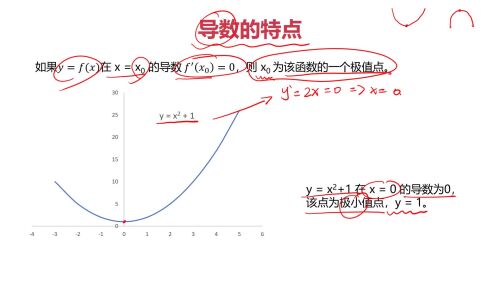 查看全部
查看全部 -
题目:

用到的lib:

代码(已验证):
# 导入numpy库
import numpy as np
# 利用array建立矩阵A
A = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
# 查看行列数
print(A.shape)
B = A
C = np.array([[1,2],[3,4],[5,6]])
D = np.array([[1],[2],[3]])
print(B,'\n',C,'\n',D)
E = A + B
F = A - B
# *注意:A*B 需要用dot来计算
G = np.dot(A, B)
H = -A
print(E,'\n',G,'\n',H)
I = np.dot(A, D)
print(I)
查看全部 -
向量基本运算
 查看全部
查看全部 -
通过老师的讲解,了解回归分析中,梯度下降法,偏导与最小二乘法拟合的a和b求解计算关系。
实例讲解很清晰易懂,逐行逐句敲代码,直到问题完全解决!非常给力,好学易懂!我是小白,一位高中信息技术教师!查看全部 -
矩阵的基本运算
相加:

互为同型矩阵才能进行加法/减法运算。
数乘:
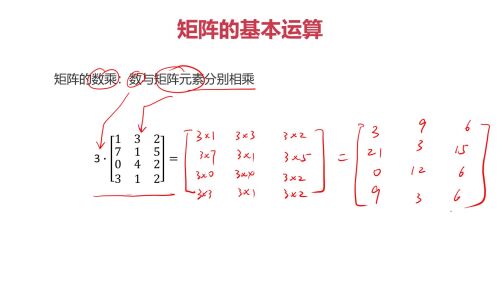
数乘的规律:

相乘:
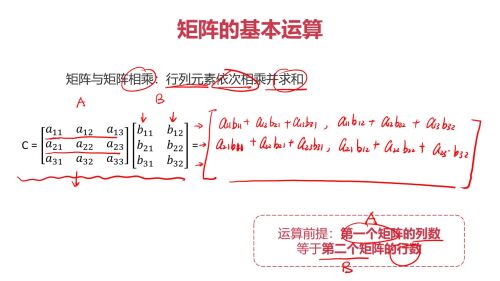
相乘规律

总结:
1. 同型矩阵:行数、列数分别相同的矩阵
2. 负矩阵:矩阵元素互为相反数关系的矩阵(负矩阵必定为同型矩阵)
3. 矩阵的加法:矩阵元素分别相加(互为同型矩阵才能进行加法运算)
4. 矩阵的加法满足交换律、结合律,即:
A+B=B+A
A+B+C=A+(B+C)
矩阵的减法可以理解为对负矩阵的加法,即:
A-B=A+(-B)
5. 矩阵的数乘:数与矩阵元素分别相乘
6. 矩阵的数乘满足交换律、结合律、分配律
7. 矩阵与矩阵相乘:行列元素依次相乘并求和(第一个矩阵列数等于第二个矩阵行数)
8. 矩阵与矩阵相乘不满足交换律,满足结合律、分配律
查看全部 -
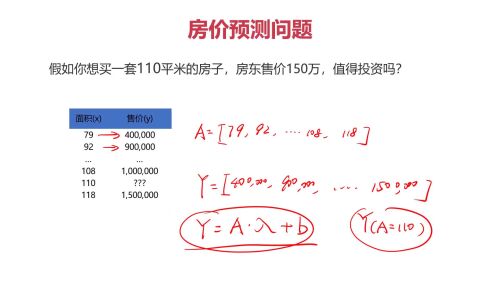
机器学习三大数学:1.微积分 2.概率论 3.矩阵
一.矩阵使用的例子:
1. 图片。在计算机中,用矩阵表示图片。
2. 用户信息列表。一行表示一个人,一列表示一个属性。
二.微积分
1.微分表示 切线斜度。可以帮我们找到,曲线的最小值(切线斜度为0)。比如 用梯度下降做线性回归。
2.积分表示面积。在 预测概率时,会用到。
三.概率
预测,其实就是概率。
查看全部 -
 案例查看全部
案例查看全部 -
 全概率公式查看全部
全概率公式查看全部
举报




