故事背景
人物
-
大牛
-
小白
-
新晋人群 — 广场舞天团: 常年汇聚在各大广场,不间断更新舞种的广场舞领军人物……

场景
广场上疲惫的大牛和小白。
前言
集合”包含一堆东西“的容器,集合里的“东西”则称为元素。通过之后的学习,我们来看如何定义这个”容器“,看以下怎么操作这些”元素“。
某日黄昏,日渐西斜,小白和大牛拖着疲惫的身躯出现在某市的广场附近。
“牛哥,这天也太热了。”
“是啊,还真是有点儿不适应广西的天气。”
“咱们在这儿休息会儿再回宾馆吧。热的我走不动了。”

“好,那就休息会儿,咱们也好好欣赏一下黄昏的美景,也看一次日落。”
“得了吧牛哥,都啥时候了。还诗情画意的。歇一会儿得了呗。”
说着话,两人拖着疲惫的身躯靠在了广场的长椅上。
时间不长,两人同时响起了鼾声。
“你是我心中最美的云彩,斟满美酒让你留下来,(留下来)……”
一阵响亮的音乐声将两人惊醒。广场上,大爷大妈们随着激情的音乐声,跳着富有旋律的舞步。
"看来全国各地,哪儿的大爷大妈们都一样啊,你看这人多的。快赶上示威游行了。"小白揉着朦胧的双眼。似乎很不满意被人惊醒。
大牛并没有注意小白的小动作,眼睛一眨不眨的盯着舞蹈团。“不对啊,这个风格和北京的不太一样啊。”
“厉害啊牛哥,这都能看出来。看来牛哥也是经常混迹于广场圈的人啊。怎么样,是不是看着心痒痒了,想上去试一下?”
“不行咯不行咯,今天给我累的,哪还能跳动这个。倒是你,醒利索了没?”
“差不多了吧,咱们现在回宾馆吗,今天的工作成果还没整理。赶紧整理完就可以休息了。”
“不急不急,现在这种氛围这么和谐,正好让我看看你这两天的学习成果啊,看看你是不是只顾着玩游戏,把学习放下了?”
“哪儿能啊牛哥,最近学到特别的努力。你要是不信,我给你说说我这两天的学习成果。而且……”
“好你个小白,都这个时候了还跟你牛哥卖关子,快说,而且什么”
“好好好,我说我说,我今天要说的这个数据结构跟这个广场特别契合。”
“哦?我先不听什么数据结构,先说一下怎么跟这个广场契合吧。”
“是这样的牛哥,你看哈,这个广场上的老人们分成了三四拨。而且队形基本没有,更为重要的是每组里的大爷大妈们跳的舞步没有一个是相同的。您老猜猜,我今天想说的是什么结构?”
“哈哈,你这么一说还真是,刚才我这老眼昏花的都没仔细看。不用猜了,你想说的肯定是集合。”
“牛哥不愧是牛哥,我就说这么一点儿就能猜出来我要说什么。不过牛哥,你给我说说你是咋猜出来的。是我那句话露馅了吗?”
“你倒是没有露馅,换个不熟悉数据结构的还真让你蒙着了。幸亏我老牛深算,才没有上你的当。仔细听听哈,我给你说说我咋才出来的。”
第一点是因为老人们分为了三四拨。其实通过这个我还没猜出来,只是能联想到,没敢确定。
第二点是因为没有队形,集合里最重要的两点之一是集合中的元素是无序的。这一点让我加深了自己的判断。
第三点是因为没有一个人的舞步是相同的。集合另一个重要的点是集合中的元素是唯一的,不能重复的。
“也正是因为上面这三点,才让我确定了自己的判断,你小子今天肯定是想说集合。”
“还是牛哥最厉害,既然您都猜出来了,我也就不卖关子了。今天我确实要讲集合,我摊牌了。”
“好,我这花生、瓜子、啤酒、饮料、小马扎都准备好了,就等你开讲了。哈哈……”
“牛哥,你且听我慢慢道来……”
1. 集合
1.1 定义
-
集合是由一组无序且唯一(即不能重复)的项组成的。与数学中的有限集合概念相同
-
集合中的每个元素称为集合中的成员。
1.2 成员特点
- 确定性: 成员是否在集合中是确定的
- 互异性: 集合中不能包含相同的元素
- 无序性: 集合中的成员是无序的
1.3 逻辑结构
集合结构:集合内的成员都是没有关联的
“好了牛哥,概念说完了,下面我要自己实现一个集合了。”
“好,我看着呢,你写吧。” 坐的时间长了,大牛也是有气无力的说道。

2. 集合的实现
2.1 首先我们定义一个集合类
这里使用了一个数组作为这个集合的存储容器。因为后面有的操作使用数组会更加便捷,也是可以使用其他类型。
class Set{
constructor() {
this.data = [];
}
}
2.2 添加一些常用的方法
与其他结构类似,集合中的常用方法有,增删改查……
class Set {
constructor() {
this.data = [];
}
// 添加元素
add (value) {
if (!this.data.includes(value)) {
this.data.push(value)
}
}
// 查找元素位置
findIndex (value) {
// 因为集合中的元素都是不重复的,所以可以直接使用首次出现的下标
return this.data.indexOf(value)
}
// 删除元素
remove (value) {
if (this.data.includes(value)) {
this.data.splice(this.findIndex(value), 1)
}
return true
}
// 获取当前集合元素数量
size () {
return this.data.length;
}
// 清空当前集合
clear () {
this.data = [];
}
// 查找集合中是否含有某个元素
has (value) {
return this.data.includes(value)
}
}
“解释一下这里边比较复杂的一个 remove 方法。首先我们需要查找当前元素中是否有这个元素,如果没有则直接返回成功,如果有,则将此元素从数组中剔除,机智如我,哈哈哈哈……”
“行了,先别嘚瑟,集合中不止只有这几种方法吧,还有求集合的交集、并集、差集、子集……好多方法,你这才实现几个,就喘上了。”

“是是是,牛哥说的是,不过小弟也早有准备。这些东西我这几天可算是研究透了。”
3. 求集合的交集、并集、差集、子集
还是像刚才一样,我们先介绍一下方法的概念,然后再写方法。
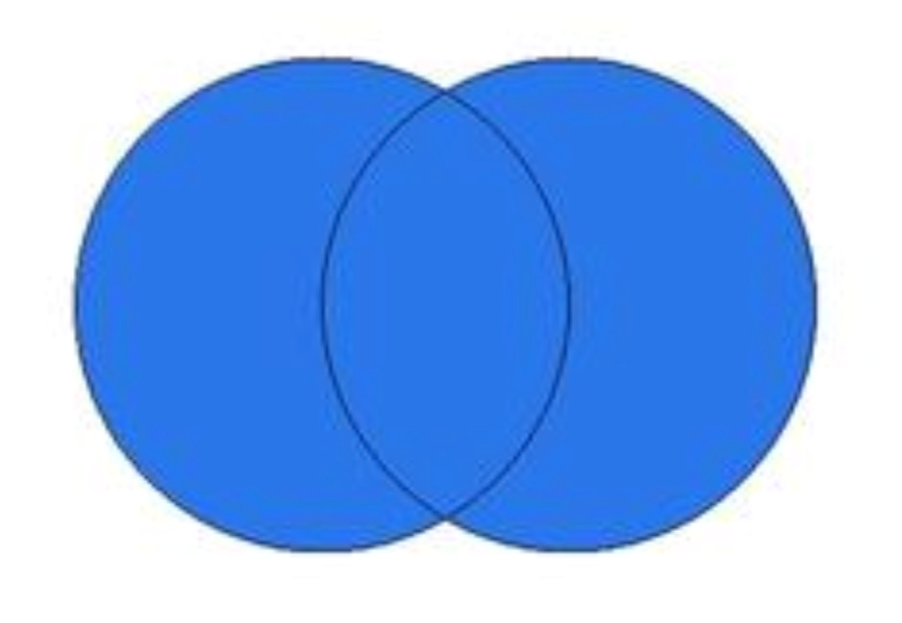
3.1 并集
对于给定的两个集合,返回一个包含两个集合中所有元素的新集合。
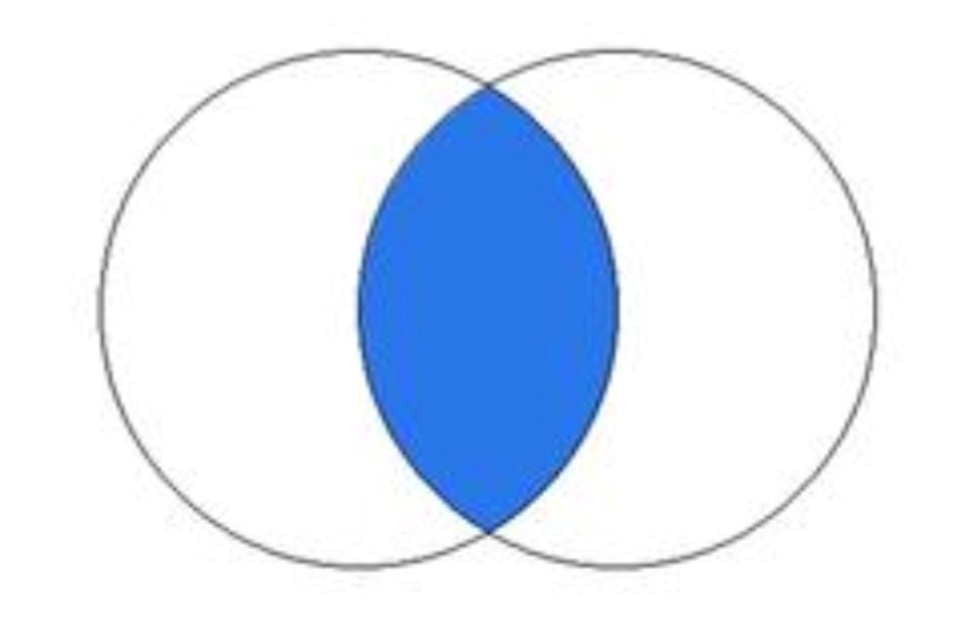
3.2 交集
对于给定的两个集合,返回一个包含两个集合中共有元素的新集合。
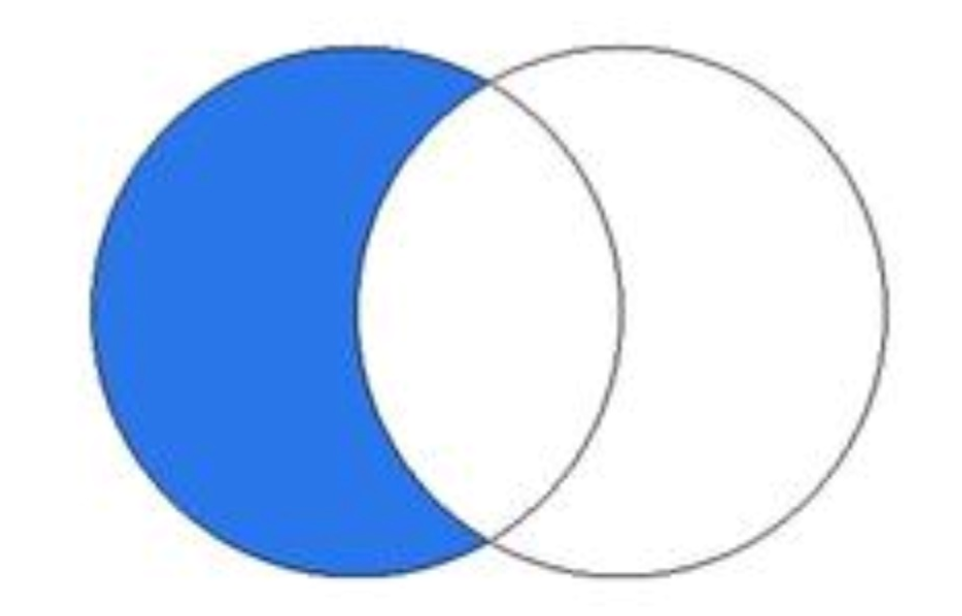
3.3 差集
对于给定的两个集合,返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合。
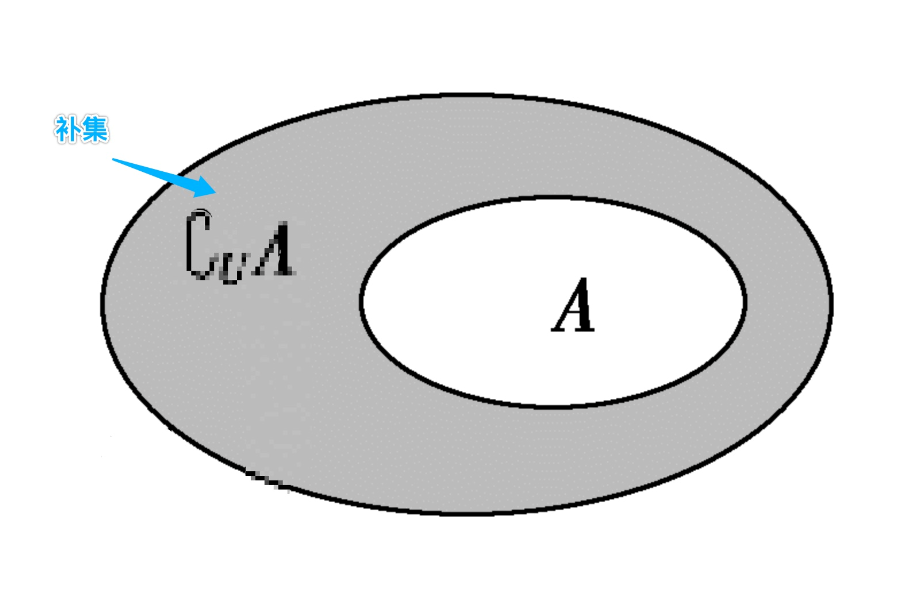
3.4 补集
对于给定的集合 A 和 B,A 为 B 的子集,返回存在于 B 且不存在于 A 中的元素。
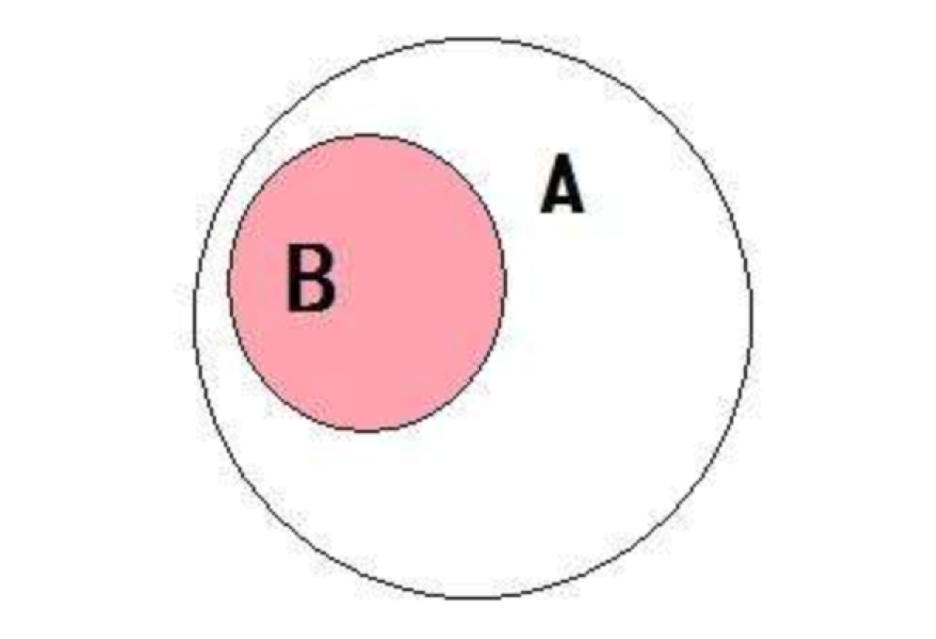
3.5 子集
验证一个给定集合是否是另一集合的子集。
class Set {
constructor() {
this.data = [];
}
// 子集
isChild (newSet) {
// newSet长度不等于当前集合长度,且newSet的每一个元素当前集合中都存在
return this.data.length !== newSet.data.length && newSet.data.every(item => this.data.indludes(item))
}
// 并集
mergeSet (newSet) {
// 如果item存在于newSet中,但是不存在当前集合中,将元素记录
newSet.forEach(item => {
if (!this.data.has(item)) {
this.data.push(item)
}
})
return this.data
}
// 差集
diffSet (newSet) {
// 返回属于当前集合但是不属于newSet集合的元素
return this.data.filter(item => !newSet.has(item))
}
// 交集
interSet (newset) {
// 返回同属于两个集合的元素
return this.data.fileter(item => newSet.has(item))
}
// 补集
complementSet (newSet) {
if (!this.isChild(newSet)) {
return false
}
return this.diffSet(newSet)
}
}
“难道说我想用个集合,还得写这么一串代码?那得又多麻烦。”
4. Set
“不是啊牛哥,ES6 中提供了一种新的数据结构 Set。就是我们说的集合结构”
4.1 方法:
- add: 添加某个值,返回Set结构本身
- delete: 删除某个值,返回一个布尔值
- has: 判断元素是不是当前集合的成员,返回一个布尔值
- clear: 清空当前集合,没有返回值
- size: 返回当前集合的成员总数
const set = new Set();
set.add(1) // 添加成员 1
set.add(2) // 添加成员 2
set.delete(1) // 删除成员 1
set.has(2) // 判断 2 是不是set的成员
set.size() // 返回set的成员总数
set.clear() // 将set的所有成员清空
4.2 遍历:
- keys: 返回键名列表
- values: 返回键值列表
- entries: 返回键值对列表
- forEach: 遍历每个成员
const set = new Set([1,2,3])
set.keys() // 1,2,3
set.values() // 1,2,3
set.entries() // [1,1] [2,2] [3,3]
set.forEach((value, key) => console.log(`${key} -> ${value}`))
// 1 -> 1
// 2 -> 2
// 3 -> 3
这里有个小技巧哟牛哥,我原来做数组去重的时候都是遍历数组,计数去重,现在有了Set就不用了。我们可以这么写:
const arr = [1,2,3,1,2,3]
arr = [...new Set(arr)] // [1,2,3]
“因为集合中的元素都是唯一的,所以这个操作之后我们可以得到一个去重的数组,这样就显得优雅多了。牛哥,你来看看。”
小白写完之后打算让大牛看下,给个评价。此时却响起了一阵不合时宜的声响。
“呼……呼……呼……”
“牛哥,你别睡啊牛哥,我们现在还得回去呢。”
“老天啊,我的命怎么这么苦啊”
“牛哥,牛哥……”
“……”
小结
本节主要讲述了
1.集合的特点和逻辑结构
2.如何操作集合中的元素
3.求集合的并、差、交、补、子集
4.JavaScript 中 set 的使用
努力学习的你,加油!!!

番外篇
面试题攻坚战 — 陆:
将一个N * N的数组实现从右上到左下打印
const arr = [
[1,2,3,4],
[5,6,7,8],
[9,10,11,12],
[13,14,15,16]
]
function rotateArr(arr) {
// 。。。一系列操作
}
// 输出的结果为
4
3,8
2,7,12
1,6,11,16
5,10,15
9,14
13
解:
function rotateArr(arr) {
let len = arr.length; // 获取到N的长度
let min = -len // 定义一个最小值为 min
for (let index = len - 1; index > min; index--) {
// 将每个index作为打印的初始值,需要从上到下打印数据
let middle = index
for (let i = 0; i < len; i++) {
if(arr[i][middle])
console.log(arr[i][middle])
}
middle ++
}
}
}
说明:
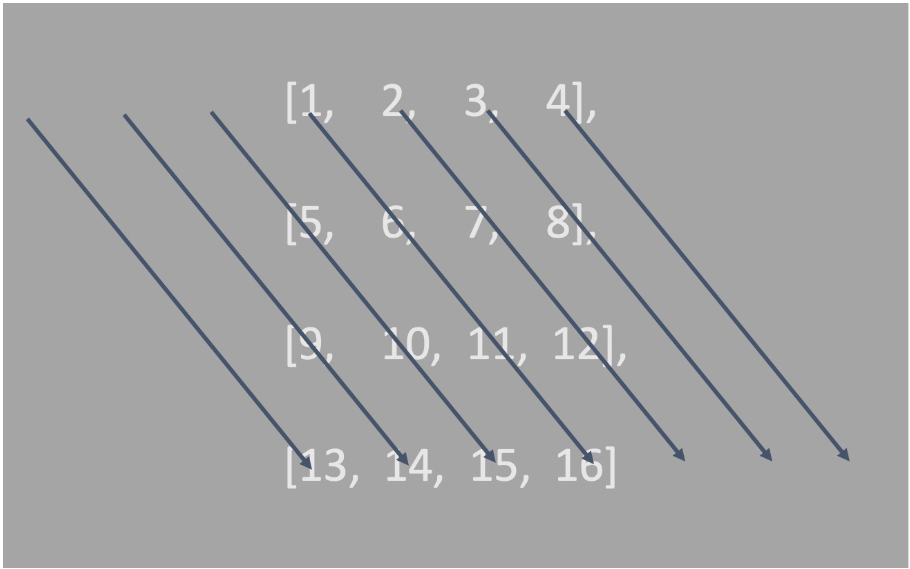
第一次遍历:
midde 从3 递增到 6, i 从0 递增到 4
对应输出为
arr[0][3] = 4
arr[1][4] = undefined
arr[2][5] = undefined
arr[3][6] = undefined
所以第一轮只输出 4
第二次遍历
midde 从2 递增到 5, i 从0 递增到 4
对应输出为
arr[0][2] = 3
arr[1][3] = 8
arr[2][4] = undefined
arr[3][5] = undefined
所以第二轮输出 3 和 8
……
最后一次遍历
midde 从 -3 递增到 0, i 从0 递增到 4
对应输出为
arr[0][-3] = undefined
arr[1][-2] = undefined
arr[2][-1] = undefined
arr[3][0] = 13
所以第最后一轮只输出13
END



