-
矩阵的数乘
查看全部 -
矩阵加减运算
查看全部 -
矩阵含义M行N列
查看全部 -
老师讲得真好
查看全部 -
实战: 利用朴素贝叶斯判断客户消费意愿
调用sklearn朴素贝叶斯模块的CategoricalNB, 训练模型基于用户信息,预测购买商品的概率。
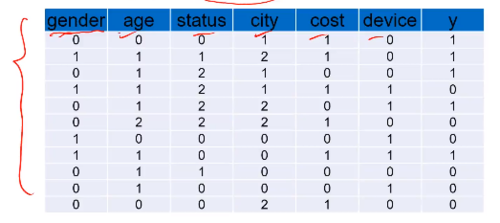
任务一:基于上面的数据,建立朴素贝叶斯模型
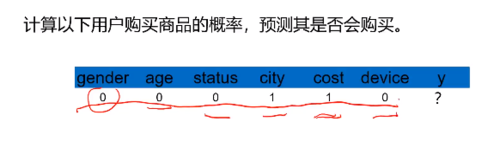
任务二:基于模型,判断上面用户会否购买
具体实现代码展示:
import pandas as pd //导入pandas库
import numpy as np //导入numpy库
data = pd.read_csv("chapter3_data.csv") //将数据预先储存为一个csv文件,然后加载到开发环境中来
data.head() //读取数据
#x赋值 x = data.drop(["y"], axis=1) //将y的一列单独去掉,axis=0为行,axis=1为列
print(x)
#y赋值 y = data.loc([: , "y"])
print(y)
#建立模型
from sklearn.naive_bayes import CategoricalNB //从sklearn包的naive_bayes之中导入 CategoricalNB
model = CategoricalNB() //建立模型实例
model.fit(x , y) //训练模型
y_predict_proba = model.predict_proba(x) //预测y=1or=0的概率
y_predict = model.predict(x) //输出y的预测值
#计算模型准确率
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y, y_predict)
print(accuracy)
任务二:
#测试样品x的预测
X_test = np.array([[0,0,0,1,1,0]]) //先将其转化成为数组形式
print(X_test)
y_predict_proba = model.predict_proba(X_test) //预测样品的购买或不购买的概率
print(y_predict_proba)
y_test = model.predict(X_test) //输出样品的预测值
print(y_test)
查看全部 -
概率分析
例子:
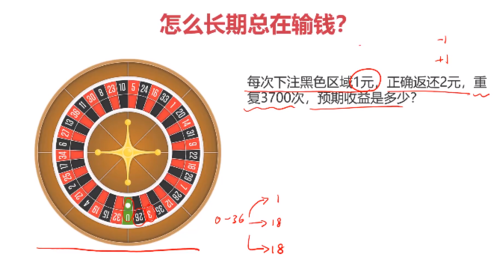
玩一次输赢的概率:
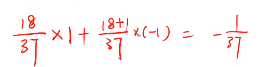
如果进行3700次:
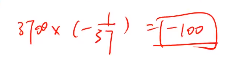
长久下去基本上都是输的
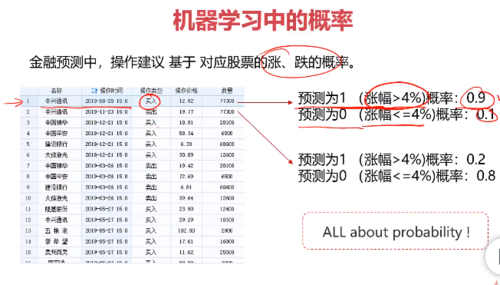
概率分析在人工智能中的应用:
分类,人面识别的情况,预测不同类别可能性的概率

>0 , 值得玩
<0, 不值得玩
在某种情况A发生下的B发生的概率: 条件概率的情况

现实的情况,就是在某种分布的条件之下计算某个事情发生的可能性

你出门的概率 1/4 ,女神出门的概率1/2 ,遇到女神的概率是1/2
全概率的情况:


总结出来

贝叶斯公式:

贝叶斯公式与全概率、条件概率公式的关系:
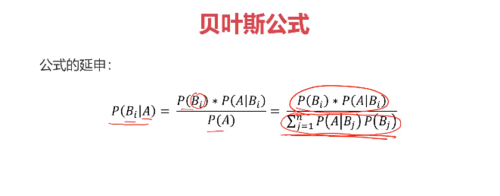
条件概率公式/全概率公式 = 贝叶斯公式

所谓的后验概率就是上面的 P( Bi | A )
朴素贝叶斯:
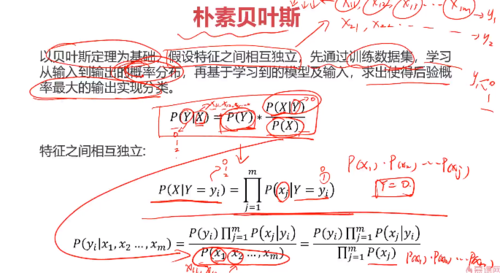
朴素贝叶斯的案例:
基于用户的性别、年龄和使用的设备,预测用户是否购买产品

yi 先计算 y=1 或 =0 的各自概率 乘以 xj|yi 计算 x1,x2, x3都为0的概率 / xj 每个x在各自组里面是0的概率
注意:y = 1 的概率和y!= 1的概率总和不为1
查看全部 -
概率分析
例子:赌博
查看全部 -
实战:python 实现函数微分与积分

具体代码展示:
import sympy as sp //导入sympy库
x = sp.Symbol("x") //告诉程序x为符号
y = 3*x**2 //定义y,*为乘,**为次方
#求导
y1 = 3*x //定义y1
f1 = sp.diff(y1) //对y1进行求导
print(f1) //打印f1结果
依次对y2,y3求导,在此省略...
#求积分
F1 = sp.integrate(f1, x) //对f1进行积分,相应函数为x
print(F1)
依次计算F2, F3的积分,此处省略...
#求极限
L1 = sp.limit(y1, x, 0) //求y1的极限,当x趋近于0时
print(L1)
依次计算L2, L3的极限,此处省略...
查看全部 -
积分:反导数
不定积分
定积分
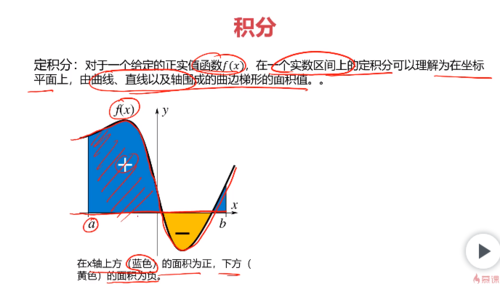
概率密度函数的概念:
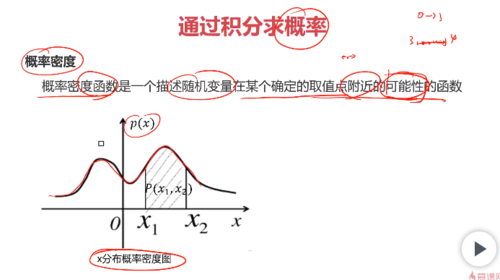 查看全部
查看全部 -
模型求解(AI相关的模型)与梯度下降法

偏导数,用于两个或以上的自变量的情况
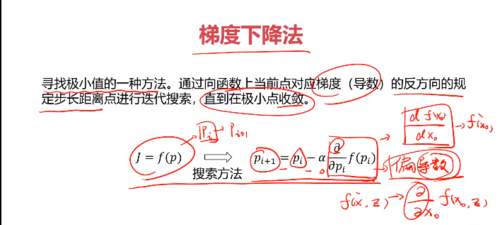
寻找适合的a 和 b 值
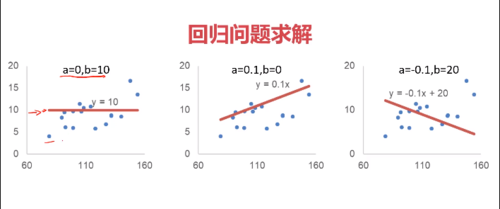
目标:尽可能使模型模拟出来的y值接近实际的y值,使两者差值的平方最小化

引入损失函数,使导数后的平方抵消,由于存在m个样品,也除以m
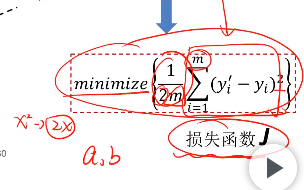
应用梯度下降法来计算收敛

最后获得一条最优解
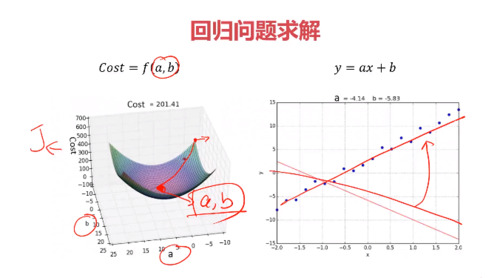 查看全部
查看全部 -
极限与导数
案例:
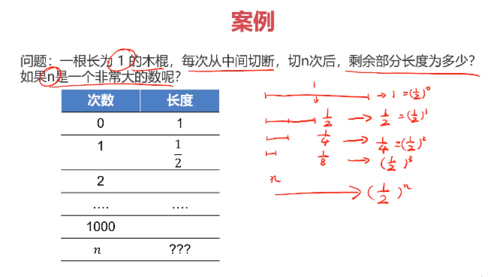
lim n-->无穷(1/2)^n 越接近 0
当n 次数越多,接近正无穷时,整个数越接近 0
极限的定义:当函数中的某个变量在不断变大或者变小的无限过程中,函数逐渐逼近于某一确定数值的过程,其中这种不断地永不停止地逼近某点的趋势,就是极限。
求极限的例子:

导数的基本概念 :
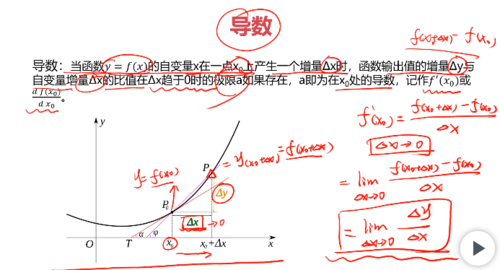 查看全部
查看全部 -
python 中AI的常用库
matplotlib : python基础绘图库,几行代码可生成绘图、直方图、条形图、散点图。
pandas : 强大的分析结构化数据的工具集,快速实现数据导入、导出、索引。
Numpy : 使用Python进行科学计算的软件包,核心是基于N维数组对象 ndarray 的数组运算。
实战 : python 实现矩阵运算

代码 :
import numpy as np //导入numpy库
A = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]]) //利用array建立矩阵A
print( A . shape) //查看行列数
依次用np.array() 建立矩阵B-D...此处省略
E = A + B
F = A - B
G = np.dot(A, B) //*注意:A*B 需要用dot来计算
H = -A
用 print() 依次打印 E, F, G, H...此处省略
I = np.dot(A, D)
print(I)
查看全部 -
房价预测的模型:因子和房价存在线性关系
则 y =a x + b
深度学习中的矩阵运算
根据用户信息 ,预测是否消费,模仿人的神经结构系统建立深度学习模型
深度学习的基本框架 : A^2 = x * theta^1, y = A* theta^2
查看全部 -
AB ^T
负矩阵、同型矩阵
加法满足交换律、结合律
乘法满足交换律、结合律、分配律
乘法矩阵不满足交换律,但满足结合律、分配律
矩阵加法、矩阵数乘、矩阵乘法
向量:矩阵的特殊情况
只有一行或一列的矩阵,亦称为向量
矩阵乘向量还是向量
例子:房屋面积和价格存在线性关系 Y=aX+b
查看全部 -
555查看全部
举报





