如何在pygame中找到三角形的中点，然后递归地重复执行它以形成谢尔宾斯基三角形？

Question

如何找到最初绘制的三角形的中点？我需要创建一个谢尔宾斯基三角形，其中一个三角形内有多个三角形。到目前为止，我有第一个三角形的代码，如下所示：import pygamepygame.init()colors = [pygame.Color(0, 0, 0, 255),       # Black          pygame.Color(255, 0, 0, 255),     # Red          pygame.Color(0, 255, 0, 255),     # Green          pygame.Color(0, 0, 255, 255),     # Blue          pygame.Color(255, 255, 255, 255)] # White# Each of these constants is the index to the corresponding pygame Color object# in the list, colors, defined above.BLACK = 0RED = 1GREEN = 2BLUE = 3WHITE = -1height = 640width = 640size = [width, height]screen = pygame.display.set_mode(size)screen.fill(WHITE)def draw_triangle(p1, p2, p3, color, line_width, screen):    p1 = [5, height - 5]    p2 = [(width - 10) / 2, 5]    p3 = [width - 5, height - 5]    pygame.draw.polygon(screen, 0, [p1, p2, p3], 2)    pygame.display.flip()def find_midpoint(p1, p2):def sierpinski(degree, p1, p2, p3, color, line_width, screen):剩下的两个函数都是完成谢尔宾斯基三角形所需要的。首先，创建一个函数来查找中点，然后创建一个在这些三角形内创建多个三角形（称为谢尔宾斯基三角形）的函数。

Answer 1

另一个三角形内的“中点三角形”由一个三角形定义，该三角形的坐标是周围三角形各边的中点：

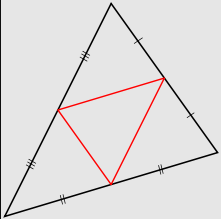
因此，对于三角形的每条线/边，计算中点：

def lineMidPoint( p1, p2 ):

    """ Return the mid-point on the line p1 to p2 """

    # Ref: https://en.wikipedia.org/wiki/Midpoint

    x1, y1 = p1

    x2, y2 = p2

    x_mid = round( ( x1 + x2 ) / 2 )

    y_mid = round( ( y1 + y2 ) / 2 )

    return ( x_mid, y_mid )

在您的情况下，这将被多次调用p1,p2并p3生成 3 个“角”三角形：

# midpoints of each size

mid_p1 = lineMidPoint( p1, p2 )

mid_p2 = lineMidPoint( p2, p3 )

mid_p3 = lineMidPoint( p3, p1 ) 

# The 3 "corner" triangles

upper_triangle = [ mid_p1, p2, mid_p2 ]

left_triangle  = [ p1, mid_p1, mid_p3 ]

right_triangle = [ mid_p3, mid_p2, p3 ]

# The inner triangle (for the sake of completeness)

inner_triangle = [ mid_p1, mid_p2, mid_p3 ]

然后，您需要将其包装在递归调用中，并进行某种深度救助。

就像是：

def drawTriangle( window, colour, points, bailout=5 ):

    if ( bailout > 0 ):

        # Calculate the 3 inner corner-triangles

        p1, p2, p3 = points

        mid_p1 = lineMidPoint( p1, p2 )

        mid_p2 = lineMidPoint( p2, p3 )  # mid-point of each side

        mid_p3 = lineMidPoint( p3, p1 ) 

        # triangles between the original corners, and new mid-points

        upper_triangle = [ mid_p1, p2, mid_p2 ]  

        left_triangle  = [ p1, mid_p1, mid_p3 ]

        right_triangle = [ mid_p3, mid_p2, p3 ]

        drawTriangle( window, colour, upper_triangle, bailout-1 )

        drawTriangle( window, colour, left_triangle,  bailout-1 )

        drawTriangle( window, colour, right_triangle, bailout-1 )

    else:

        pygame.draw.lines( window, colour, True, points )  # draw triangle

我认为这画出了一个谢尔宾斯基三角形

Answer 2

我不确定争论的目的degree是什么，也许是为了限制递归深度？

这是一个基于您的问题的示例，使用递归 sierpinski 函数：

import pygame

def draw_triangle(p1, p2, p3, color, line_width, screen):

    pygame.draw.polygon(screen, color, [p1, p2, p3], line_width)

def midpoint(p1, p2):

    """ Return the mid-point on the line p1 to p2 """

    x1, y1 = p1

    x2, y2 = p2

    x_mid = (x1 + x2) // 2

    y_mid = (y1 + y2) // 2

    return (x_mid, y_mid)

def sierpinski(degree, p1, p2, p3, color, line_width, screen):

    # p1 → bottom left, p2 → bottom right, p3 → top

    # recursive function so check for exit condition first

    if abs(p1[0] - p2[0]) <= 2 and abs(p2[0] - p3[0]) <= 2 and abs(p1[0] - p3[0]) <= 2:

        return

    draw_triangle(p1, p2, p3, color, line_width, screen)

    a = midpoint(p1, p2)

    b = midpoint(p1, p3)

    c = midpoint(p2, p3)

    # skip the centre triangle

    sierpinski(degree, p1, a, b, color, line_width, screen)

    sierpinski(degree, p2, a, c, color, line_width, screen)

    sierpinski(degree, p3, b, c, color, line_width, screen)

height = 640

width = 640

pygame.init()

screen = pygame.display.set_mode((width, height), pygame.RESIZABLE)

pygame.display.set_caption("Sierpiński")

clock = pygame.time.Clock()

update_screen = True

running = True

while running:

    for event in pygame.event.get():

        if event.type == pygame.QUIT:

            running = False

        elif event.type == pygame.VIDEORESIZE:

            width, height = event.dict["size"]

            screen = pygame.display.set_mode((width, height), pygame.RESIZABLE)

            update_screen = True

    if update_screen:

        # only draw the screen when required

        screen.fill(pygame.color.Color("white"))

        # determine initial points based on window size

        p1 = [5, height - 5]

        p2 = [(width - 10) // 2, 5]

        p3 = [width - 5, height - 5]

        sierpinski(None, p1, p2, p3, pygame.color.Color("black"), 1, screen)

        pygame.display.update()

        update_screen = False

    # limit framerate

    clock.tick(30)

pygame.quit()

为了简洁起见，我删除了颜色处理，而是使用pygame.color.Color接受其构造函数的字符串参数。我还使用整数除法//来代替round(…).

根据递归函数的深度或复杂性，您可以重新绘制每一帧，但我想展示一个限制示例，以防函数复杂性增加。最后，我最近一直在调整屏幕大小，这似乎与一次绘制有关，所以我也将其包括在内。

编辑：我修改了该sierpinski函数以支持degree指定递归 dep 的参数

def sierpinski(degree, p1, p2, p3, color, line_width, screen):

    # p1 → bottom left, p2 → bottom right, p3 → top

    # recursive function so check for exit condition first

    if degree is None:

        if abs(p1[0] - p2[0]) <= 2 and abs(p2[0] - p3[0]) <= 2 and abs(p1[0] - p3[0]) <= 2:

            return

    else:

        if degree == 0:

            return

        else:

            degree -= 1

    …

然后我添加了一些事件处理，以便可以使用鼠标滚轮来增加和减少度数，这显示在标题栏上：

elif event.type == pygame.MOUSEBUTTONUP:

    if event.button == 4:  # wheel up

        if degree is None:

            degree = 8

        else:

            degree += 1

            if degree > maximum_degree:

                degree = maximum_degree

        update_screen = True

    elif event.button == 5: # wheel down

        if degree is None:

            degree = 3

        else:

            degree -= 1

            if degree < minimum_degree:

                degree = minimum_degree

        update_screen = True

…