傅里叶变换和过滤给定的数据集

Question

总的来说，我想计算给定数据集的傅里叶变换并过滤掉一些具有最大绝对值的频率。所以：1)给定一个带有时间 t 的数据数组 D，2)找到 k 个最大的傅里叶系数，3)从数据中删除这些系数，以便从原始数据中滤除某些信号。在绘制给定时间内过滤后的数据集时，最终会出现问题。我不太确定错误在哪里。最终的“过滤数据”图看起来甚至没有稍微平滑，并且与原始数据相比以某种方式改变了其位置。我的代码完全糟糕吗？第1部分）：n = 1000limit_low = 0limit_high = 0.48D = np.random.normal(0, 0.5, n) + np.abs(np.random.normal(0, 2, n) * np.sin(np.linspace(0, 3*np.pi, n))) + np.sin(np.linspace(0, 5*np.pi, n))**2 + np.sin(np.linspace(1, 6*np.pi, n))**2scaling = (limit_high - limit_low) / (max(D) - min(D))D = D * scalingD = D + (limit_low - min(D))                       # given datat = linspace(0,D.size-1,D.size)                    # times第2部分）：from numpy import linspace                                    import numpy as npfrom scipy import fft, ifftD_f = fft.fft(D)         # fft of D-dataset#---extract the k biggest coefficients out of D_f ---k = 15I, bigvals = [], []                                        for i in np.argsort(-D_f):                    if D_f[i] not in bigvals:                    bigvals.append(D_f[i])                  I.append(i)        if len(I) == k:            breakbigcofs = np.zeros(len(D_f))             bigcofs[I] = D_f[I]                      # array with only zeros in in except for the k maximal coefficients第 3 部分）：D_filter = fft.ifft(bigcofs)D_new = D - D_filterp1=plt.plot(t,D,'r')p2=plt.plot(t,D_new,'b');plt.legend((p1[0], p2[0]), ('original data', 'filtered data'))感谢您的帮助，提前致谢。

Answer 1

我注意到两个问题：

1. 您可能想要具有最大绝对值的分量，因此而np.argsort(-np.abs(D_f))不是np.argsort(-D_f).

2. 更巧妙的是：bigcofs = np.zeros(len(D_f))是类型float64并且丢弃了行 处的虚部bigcofs[I] = D_f[I]。你可以用以下方法解决这个问题bigcofs = np.zeros(len(D_f), dtype=complex)

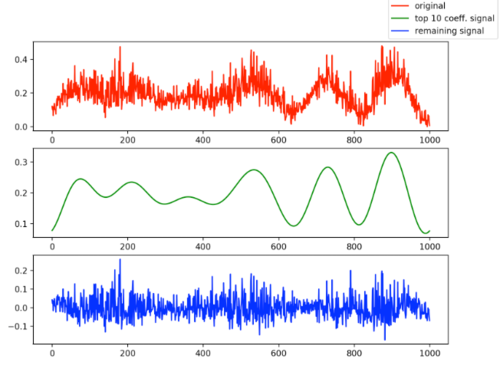
我在下面稍微改进了您的代码以获得所需的结果：

import numpy as np

from scipy import fft, ifft

import matplotlib.pyplot as plt

n = 1000

limit_low = 0

limit_high = 0.48

N_THRESH = 10

D = 0.5*np.random.normal(0, 0.5, n) + 0.5*np.abs(np.random.normal(0, 2, n) * np.sin(np.linspace(0, 3*np.pi, n))) + np.sin(np.linspace(0, 5*np.pi, n))**2 + np.sin(np.linspace(1, 6*np.pi, n))**2

scaling = (limit_high - limit_low) / (max(D) - min(D))

D = D * scaling

D = D + (limit_low - min(D))                       # given data

t = np.linspace(0,D.size-1,D.size)                    # times

# transformed data

D_fft = fft.fft(D)

# Create boolean mask for N largest indices

idx_sorted = np.argsort(-np.abs(D_fft))

idx = idx_sorted[0:N_THRESH]

mask = np.zeros(D_fft.shape).astype(bool)

mask[idx] = True

# Split fft above, below N_THRESH points:

D_below = D_fft.copy()

D_below[mask] = 0

D_above = D_fft.copy() 

D_above[~mask] = 0

#inverse separated functions

D_above = fft.ifft(D_above)

D_below = fft.ifft(D_below)

# plot

plt.ion()

f, (ax1, ax2, ax3) = plt.subplots(3,1)

l1, = ax1.plot(t, D, c="r", label="original")

l2, = ax2.plot(t, D_above, c="g", label="top {} coeff. signal".format(N_THRESH))

l3, = ax3.plot(t, D_below, c="b", label="remaining signal")

f.legend(handles=[l1,l2,l3])

plt.show()