从时间序列数据确定傅立叶系数

Question

我问了一个关于如何从时间序列数据确定傅立叶系数的已删除问题。我重新提交这个问题是因为我已经更好地阐述了这个问题，并且有一个解决方案，我将给出这个解决方案，因为我认为其他人可能会发现这非常有用。我有一些时间序列数据，我已将它们分箱到等间隔的时间箱中（这一事实对我的解决方案至关重要），并且从这些数据中我想确定最能描述数据的傅里叶级数（或任何函数，实际上） 。这是一个带有一些测试数据的 MWE，用于显示我想要拟合的数据：import numpy as npimport matplotlib.pyplot as plt# Create a dependent test variable to define the x-axis of the test data.test_array = np.linspace(0, 1, 101) - 0.5# Define some test data to try to apply a Fourier series to.test_data = [0.9783883464566918, 0.979599093567252, 0.9821424606299206, 0.9857575507812502, 0.9899278899999995,             0.9941848228346452, 0.9978438300395263, 1.0003009205426352, 1.0012208923679058, 1.0017130521235522,             1.0021799664031628, 1.0027475606936413, 1.0034168260869563, 1.0040914266144825, 1.0047781181102355,             1.005520348837209, 1.0061899214145387, 1.006846206627681, 1.0074483048543692, 1.0078691461988312,             1.008318736328125, 1.008446947572815, 1.00862051262136, 1.0085134881422921, 1.008337095516569,             1.0079539881889774, 1.0074857334630352, 1.006747783037474, 1.005962048923679, 1.0049115434782612,             1.003812267822736, 1.0026427549407106, 1.001251963531669, 0.999898555335968, 0.9984976286266923,             0.996995982142858, 0.9955652088974847, 0.9941647321428578, 0.9927727076023389, 0.9914750532544377,             0.990212467710371, 0.9891098035363466, 0.9875998927875242, 0.9828093773946361, 0.9722532524271845,             0.9574084365384614, 0.9411012303149601, 0.9251820309477757, 0.9121488392156851, 0.9033119748549322,             0.9002445803921568, 0.9032760564202343, 0.91192435882353, 0.9249696964980555, 0.94071381372549,]# Create a figure to view the data.fig, ax = plt.subplots(1, 1, figsize=(6, 6))# Plot the data.ax.scatter(test_array, test_data, color="k", s=1)输出如下：问题是如何确定最能描述该数据的傅里叶级数。确定傅里叶系数的常用公式需要在积分中插入一个函数，但如果我有一个函数来描述数据，我根本不需要傅里叶系数；找到这个系列的全部目的是获得数据的函数表示。如果没有这样的函数，那么，系数是如何找到的呢？

Answer 1

我对这个问题的解决方案是使用 NumPy 的快速傅里叶变换实现 numpy.fft.fft() 对数据应用离散傅里叶变换；这就是为什么数据在时间上均匀分布至关重要，因为 FFT 需要这样做。虽然 FFT 通常用于执行频谱分析，但所需的傅立叶系数与该函数的输出直接相关。

具体来说，该函数输出一系列i个复值系数c。傅立叶级数系数可使用以下关系式求得：

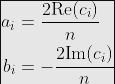
因此，FFT 允许直接计算傅立叶系数。这是我解决这个问题的 MWE，扩展了上面给出的示例：

import numpy as np

import matplotlib.pyplot as plt

# Set the number of equal-time bins to create.

n_bins = 101

# Set the number of Fourier coefficients to use.

n_coeff = 51

# Define a function to generate a Fourier series based on the coefficients determined by the Fast Fourier Transform.

# This also includes a series of phases x to pass through the function.

def create_fourier_series(x, coefficients):

    # Begin the series with the zeroeth-order Fourier coefficient.

    fourier_series = coefficients[0][0] / 2

    # Now generate the first through n_coeff'th terms.  The period is defined to be 1 since we're operating in phase

    # space.

    for n in range(1, n_coeff):

        fourier_series += (fourier_coeff[n][0] * np.cos(2 * np.pi * n * x) + fourier_coeff[n][1] * 

                           np.sin(2 * np.pi * n * x))

    return fourier_series

# Create a dependent test variable to define the x-axis of the test data.

test_array = np.linspace(0, 1, n_bins) - 0.5

# Define some test data to try to apply a Fourier series to.

test_data = [0.9783883464566918, 0.979599093567252, 0.9821424606299206, 0.9857575507812502, 0.9899278899999995,

             0.9941848228346452, 0.9978438300395263, 1.0003009205426352, 1.0012208923679058, 1.0017130521235522,

             1.0021799664031628, 1.0027475606936413, 1.0034168260869563, 1.0040914266144825, 1.0047781181102355,

             1.005520348837209, 1.0061899214145387, 1.006846206627681, 1.0074483048543692, 1.0078691461988312,

             1.008318736328125, 1.008446947572815, 1.00862051262136, 1.0085134881422921, 1.008337095516569,

             1.0079539881889774, 1.0074857334630352, 1.006747783037474, 1.005962048923679, 1.0049115434782612,

             1.003812267822736, 1.0026427549407106, 1.001251963531669, 0.999898555335968, 0.9984976286266923,

             0.996995982142858, 0.9955652088974847, 0.9941647321428578, 0.9927727076023389, 0.9914750532544377,

             0.990212467710371, 0.9891098035363466, 0.9875998927875242, 0.9828093773946361, 0.9722532524271845,

             0.9574084365384614, 0.9411012303149601, 0.9251820309477757, 0.9121488392156851, 0.9033119748549322,

             0.9002445803921568, 0.9032760564202343, 0.91192435882353, 0.9249696964980555, 0.94071381372549,

             0.957139088974855, 0.9721083392156871, 0.982955287937743, 0.9880613320235758, 0.9897455322896282,

             0.9909590626223097, 0.9922601592233015, 0.9936513112840472, 0.9951442427184468, 0.9967071285988475,

             0.9982921493123781, 0.9998775465116277, 1.001389230174081, 1.0029109110251453, 1.0044033691406251,

             1.0057110841487276, 1.0069551867704276, 1.008118776264591, 1.0089884470588228, 1.0098663972602735,

             1.0104514566473979, 1.0109849223300964, 1.0112043902912626, 1.0114717968750002, 1.0113343036750482,

             1.0112205972495087, 1.0108811786407768, 1.010500276264591, 1.0099054552529192, 1.009353759223301,

             1.008592596116505, 1.007887223091976, 1.0070715634615386, 1.0063525891472884, 1.0055587861271678,

             1.0048733732809436, 1.0041832862669238, 1.0035913326848247, 1.0025318871595328, 1.000088536345776,

             0.9963596140350871, 0.9918380684931506, 0.9873937281553398, 0.9833394624277463, 0.9803621496062999,

             0.9786476100386117]

# Determine the fast Fourier transform for this test data.

fast_fourier_transform = np.fft.fft(test_data[n_bins / 2:] + test_data[:n_bins / 2])

# Create an empty list to hold the values of the Fourier coefficients.

fourier_coeff = []

# Loop through the FFT and pick out the a and b coefficients, which are the real and imaginary parts of the

# coefficients calculated by the FFT.

for n in range(0, n_coeff):

    a = 2 * fast_fourier_transform[n].real / n_bins

    b = -2 * fast_fourier_transform[n].imag / n_bins

    fourier_coeff.append([a, b])

# Create the Fourier series approximating this data.

fourier_series = create_fourier_series(test_array, fourier_coeff)

# Create a figure to view the data.

fig, ax = plt.subplots(1, 1, figsize=(6, 6))

# Plot the data.

ax.scatter(test_array, test_data, color="k", s=1)

# Plot the Fourier series approximation.

ax.plot(test_array, fourier_series, color="b", lw=0.5)

输出如下：

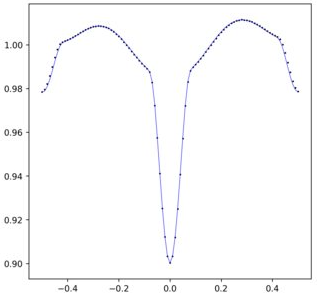
请注意，我如何定义 FFT（导入数据的后半部分，然后导入前半部分）是该数据生成方式的结果。具体来说，数据从 -0.5 到 0.5 运行，但 FFT 假设它从 0.0 运行到 1.0，因此需要进行此转换。

我发现这对于不包含非常尖锐和狭窄不连续性的数据非常有效。我很想听听是否有人对这个问题有其他建议的解决方案，我希望人们发现这个解释清晰且有帮助。

Answer 2

不确定它是否对您有帮助；我写了一个程序来插入你的数据。这是使用 Buildingblocks==0.0.15 完成的

请看下面，

import matplotlib.pyplot as plt

from buildingblocks import bb

import numpy as np

Ydata = [0.9783883464566918, 0.979599093567252, 0.9821424606299206, 0.9857575507812502, 0.9899278899999995,

             0.9941848228346452, 0.9978438300395263, 1.0003009205426352, 1.0012208923679058, 1.0017130521235522,

             1.0021799664031628, 1.0027475606936413, 1.0034168260869563, 1.0040914266144825, 1.0047781181102355,

             1.005520348837209, 1.0061899214145387, 1.006846206627681, 1.0074483048543692, 1.0078691461988312,

             1.008318736328125, 1.008446947572815, 1.00862051262136, 1.0085134881422921, 1.008337095516569,

             1.0079539881889774, 1.0074857334630352, 1.006747783037474, 1.005962048923679, 1.0049115434782612,

             1.003812267822736, 1.0026427549407106, 1.001251963531669, 0.999898555335968, 0.9984976286266923,

             0.996995982142858, 0.9955652088974847, 0.9941647321428578, 0.9927727076023389, 0.9914750532544377,

             0.990212467710371, 0.9891098035363466, 0.9875998927875242, 0.9828093773946361, 0.9722532524271845,

             0.9574084365384614, 0.9411012303149601, 0.9251820309477757, 0.9121488392156851, 0.9033119748549322,

             0.9002445803921568, 0.9032760564202343, 0.91192435882353, 0.9249696964980555, 0.94071381372549,

             0.957139088974855, 0.9721083392156871, 0.982955287937743, 0.9880613320235758, 0.9897455322896282,

             0.9909590626223097, 0.9922601592233015, 0.9936513112840472, 0.9951442427184468, 0.9967071285988475,

             0.9982921493123781, 0.9998775465116277, 1.001389230174081, 1.0029109110251453, 1.0044033691406251,

             1.0057110841487276, 1.0069551867704276, 1.008118776264591, 1.0089884470588228, 1.0098663972602735,

             1.0104514566473979, 1.0109849223300964, 1.0112043902912626, 1.0114717968750002, 1.0113343036750482,

             1.0112205972495087, 1.0108811786407768, 1.010500276264591, 1.0099054552529192, 1.009353759223301,

             1.008592596116505, 1.007887223091976, 1.0070715634615386, 1.0063525891472884, 1.0055587861271678,

             1.0048733732809436, 1.0041832862669238, 1.0035913326848247, 1.0025318871595328, 1.000088536345776,

             0.9963596140350871, 0.9918380684931506, 0.9873937281553398, 0.9833394624277463, 0.9803621496062999,

             0.9786476100386117]

Xdata=list(range(0,len(Ydata)))

Xnew=list(np.linspace(0,len(Ydata),200))

Ynew=bb.interpolate(Xdata,Ydata,Xnew,40)

plt.figure()

plt.plot(Xdata,Ydata)

plt.plot(Xnew,Ynew,'*')

plt.legend(['Given Data', 'Interpolated Data'])

plt.show()

如果你想进一步编写代码，我也给出了代码，以便你可以查看源代码并学习：

import module

import inspect

src = inspect.getsource(module)

print(src)