在图形上打印拟合详细信息并绘制多项式拟合

Question

两部分问题：通过一堆拼凑在一起的谷歌搜索，我设法将Python中的代码粘合在一起，以获取列表的日志并将其与原始列表进行比较，并应用最佳拟合的线性线（下面的代码，合成数据） 。我将如何在图表本身上打印此线性拟合的详细信息（例如梯度、y 截距、卡方）？我如何修改代码以对多项式拟合（例如 x^2 线）执行相同的操作？import numpy as npimport matplotlib.pyplot as pltfrom scipy.optimize import curve_fitfrom numpy import exp, loadtxt, pi, sqrt, random, linspacefrom lmfit import Modelimport glob, osx=[2,3,5,7,11,13,17,19,23,29,31]y=np.log10(x)print(y)plt.scatter(x, y, label="prime-logs", color="red",            marker="1", s=50)plt.xlabel('Primes')plt.ylabel('Log10 Primes')plt.title('Non-Log Plot of Log Prime v Prime')plt.legend()plt.plot(np.unique(x), np.poly1d(np.polyfit(x, y, 1))(np.unique(x)))plt.show()

Answer 1

这是一个解决方案。此处仅显示卡方（作为残差平方和）。注意，这里不存在梯度下降，np.polyfit因为问题是最小二乘问题，可以直接用SVD伪逆矩阵计算来解决。

使用允许您提取反演的每个步骤的算法（使用梯度下降或任何其他优化器），将允许您在同一图上显示拟合的每个步骤。

import numpy as np

import matplotlib.pyplot as plt

from scipy.optimize import curve_fit

from numpy import exp, loadtxt, pi, sqrt, random, linspace

# from lmfit import Model

import glob, os

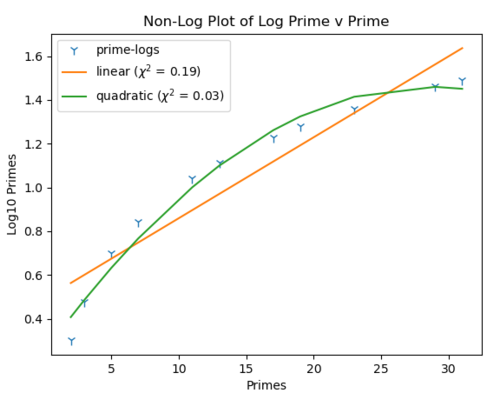
x = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]

y = np.log10(x)

print(y)

plt.plot(x, y, "1", ms=8, label="prime-logs")

y1, r, *_ = np.polyfit(x, y, 1, full=True)

f1 = np.poly1d(y1)

plt.plot(x, f1(x), label=f"linear ($\chi^2$ = {r[0]:0.2f})")

y2, r, *_ = np.polyfit(x, y, 2, full=True)

f2 = np.poly1d(y2)

plt.plot(x, f2(x), label=f"quadratic ($\chi^2$ = {r[0]:0.2f})")

plt.xlabel("Primes")

plt.ylabel("Log10 Primes")

plt.title("Non-Log Plot of Log Prime v Prime")

plt.legend()