1 回答
TA贡献1829条经验 获得超7个赞
不确定,为什么你认为这是 CDF 图。如果在 X 轴上放置概率,在 Y 轴上绘制x,它看起来像分位数图。
我没有在 Python/Matplotlib 中看到内置的此类比例,logit看起来像是最佳近似值。
或者我误解了你的问题?
代码,Python 3.8 x64 Win10
import numpy as np
import matplotlib.pyplot as plt
# exponential distribution
def PDF(x, λ):
return λ*np.exp(-λ*x)
def CDF(x, λ):
return 1.0 - np.exp(-λ*x)
def Q(p, λ): # quantile
x = -np.log(1.0 - p)/λ
return x
# plots
λ = 0.04
p = np.linspace(0.01, 0.99, 101)
x = Q(p, λ)
fig = plt.figure()
ax = fig.add_subplot(2, 1, 1)
ax.set_xscale('logit')
ax.plot(p, x, 'r-')
plt.show()
你会得到类似的东西
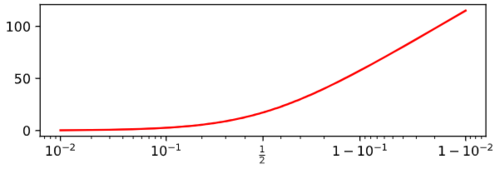
更新
如果您需要概率图,这里是
代码
from scipy.stats import expon
rve = expon(loc=0.0, scale=1.0/λ)
p = np.linspace(0.01, 0.99, 101)
x = rve.ppf(p) # Q(p, λ)
q = rve.rvs(size = 10000)
fig = plt.figure()
ax = fig.add_subplot(2, 1, 1)
res = stats.probplot(q, dist=rve, plot=ax)
plt.show()
和图表
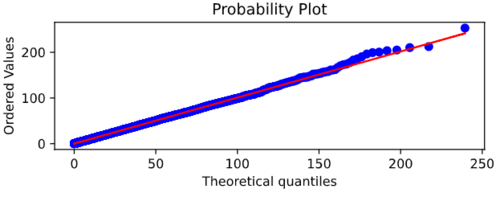
好吧,当你发送消息时我已经写好了代码。无论如何将其放置在这里,它看起来与您询问的图表完全相同 - 与自定义标签呈线性。
import matplotlib.ticker as ticker
def linear(x0, xn, y0, yn, x):
q = (x-x0)/(xn-x0)
return q * yn + (1.0 - q) * y0
pmin = 0.009
pmax = 0.991
xmin = Q(pmin, λ)
xmax = Q(pmax, λ)
x = np.linspace(xmin, xmax, 2)
p = np.linspace(pmin, pmax, 2)
tick_values = [0.01, 0.50, 0.80, 0.90, 0.96, 0.99] # probabilies
tick_names = [str(v) for v in tick_values] # ticks to place on graph
tick_xvals = [Q(p, λ) for p in tick_values] # x values for each p
tick_places = [linear(xmin, xmax, pmin, pmax, x) for x in tick_xvals] # x from linear function
fig = plt.figure()
ax = fig.add_subplot(2, 1, 1)
ax.axes.xaxis.set_major_locator(ticker.FixedLocator((tick_places)))
ax.xaxis.set_major_formatter(ticker.FixedFormatter((tick_names)))
ax.plot(p, x, 'r-')
plt.show()
和图表本身
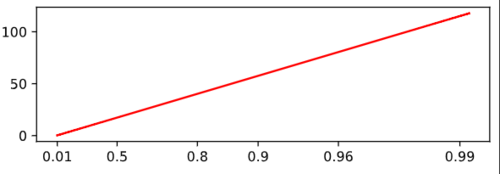
添加回答
举报
