直线和正方形之间的交点

Question

我在二维空间中有一个正方形（宽度=高度）。该正方形当前由两个点定义：BottomLeft(X1,Y1) 和 TopRight(X2,Y2)。正方形是轴对齐的，因此找到其他两个角就像 (X1, Y2) 和 (X2, Y1) 一样简单。我还有两点——一是总是在方阵内，二是肯定在方阵外。它们不一定位于广场的中心——它们可以位于任何地方。我也知道他们的坐标。我需要的是找到这两点定义的线段与正方形边之间的交点。我还想知道我与正方形的哪一边相交。给我带来麻烦的是线对角线延伸并且靠近正方形角的情况 - 例如它可以与顶线或边线相交。暴力法是尝试计算正方形每条边的交点并检查它是否存在。可以通过计算第二个点相对于正方形的位置并丢弃两条线来优化它（例如，如果 X 和 Y 坐标都增加，则无需检查正方形的底部和左侧）。我想知道是否有更好/更快的解决方案来解决我的问题？我会用Java写

Answer 1

设内点为(x0, y0)，外点为(ox, oy)

以参数形式表示线

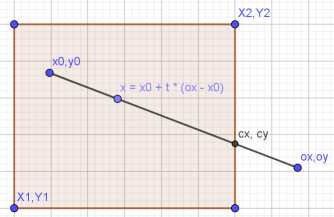
vx = ox - x0

vy = oy - y0

//equations:

x = x0 + vx * t

y = y0 + vy * t

现在根据方向找到潜在的边界位置：

if vx > 0 then

   ex = x2

else

   ex = x1

if vy > 0 then

    ey = y2

else

   ey = y1

检查水平/垂直线方向的额外情况：

 if vx = 0 then

      return cx = x0,  cy = ey

 if vy = 0 then

      return cx = ex, cy = y0

一般情况下查找与水平和垂直边缘线相交的参数

 tx = (ex - x0) / vx

 ty = (ey - y0) / vy

并获取较小参数值的交集

 if tx <= ty then //meet vertical edge first

     return cx = ex, cy = y0 + tx * vy

 else

    return  cx = x0 + ty * vx,  cy = ey

Answer 2

高效的解决方案：

我假设您知道哪个点在正方形（也可以是矩形）内。

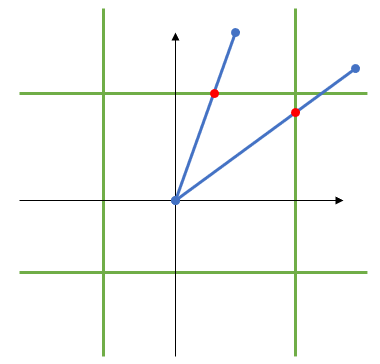
从所有其他点（第二个端点和四个角）中减去该点的坐标。考虑通过延伸正方形的边而将平面细分为九个区域。需要进行四次符号测试才能知道另一个点位于八个外部区域中的哪一个。

然后，如果该点位于“边”区域，您就隐含地知道穿过了哪边。如果该点位于“角”区域，则必须在两侧之间做出决定，这是通过检查角位于线段的哪一侧来完成的。这需要计算三角形的有符号面积（两次乘法和一次减法）。

当你知道穿过哪条边时，使用比例找到交点就很容易了。这需要一个部门。

最后，将其平移回内部点的原始位置。总成本是

• 四次减法，

• 四项标志测试，

• 对于角区域，两次乘法和一次减法，

• 一个部门，

• 两个补充

加上一点粘合逻辑。

这不能保证是绝对最小值，但必须接近。