numpy 在另一个数组中创建最大连续对的数组

Question

我有一个 numpy 数组：A = np.array([8, 2, 33, 4, 3, 6])我想要的是创建另一个数组 B，其中每个元素是 A 中 2 个连续对的成对最大值，所以我得到：B = np.array([8, 33, 33, 4, 6])关于如何实施有什么想法吗？关于如何对两个以上的元素实现这一点有什么想法吗？（同样的事情，但对于连续的 n 个元素）编辑：答案给了我一种解决这个问题的方法，但是对于n大小的窗口情况，是否有一种不需要循环的更有效的方法？编辑2：事实证明，这个问题相当于询问如何对窗口大小为 n 的列表执行 1d 最大池化。有谁知道如何有效地实施这一点？

Answer 1

成对问题的一种解决方案是使用np.maximum函数和数组切片：

B = np.maximum(A[:-1], A[1:])

Answer 2

无循环解决方案是max在由以下命令创建的窗口上使用skimage.util.view_as_windows：

list(map(max, view_as_windows(A, (2,))))

[8, 33, 33, 4, 6]

复制/粘贴示例：

import numpy as np

from skimage.util import view_as_windows

A = np.array([8, 2, 33, 4, 3, 6])

list(map(max, view_as_windows(A, (2,))))

Answer 3

在本次问答中，我们基本上要求滑动最大值。之前已经探讨过这一点 - NumPy 数组中滑动窗口中的 Max。由于我们希望提高效率，因此我们可以看得更远。其中之一是numba，这里有两个最终变体，我最终得到了杠杆parallel指令，它比没有版本提高了性能：

import numpy as np

from numba import njit, prange

@njit(parallel=True)

def numba1(a, W):

    L = len(a)-W+1

    out = np.empty(L, dtype=a.dtype)

    v = np.iinfo(a.dtype).min

    for i in prange(L):

        max1 = v

        for j in range(W):

            cur = a[i + j]

            if cur>max1:

                max1 = cur                

        out[i] = max1

    return out 

@njit(parallel=True)

def numba2(a, W):

    L = len(a)-W+1

    out = np.empty(L, dtype=a.dtype)

    for i in prange(L):

        for j in range(W):

            cur = a[i + j]

            if cur>out[i]:

                out[i] = cur                

    return out 

从之前链接的问答中，等效的 SciPy 版本将是 -

from scipy.ndimage.filters import maximum_filter1d

def scipy_max_filter1d(a, W):

    L = len(a)-W+1

    hW = W//2 # Half window size

    return maximum_filter1d(a,size=W)[hW:hW+L]

标杆管理

其他发布的通用窗口 arg 的工作方法：

from skimage.util import view_as_windows

def rolling(a, window):

    shape = (a.size - window + 1, window)

    strides = (a.itemsize, a.itemsize)

    return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)

# @mathfux's soln

def npmax_strided(a,n):

    return np.max(rolling(a, n), axis=1)

# @Nicolas Gervais's soln

def mapmax_strided(a, W):

    return list(map(max, view_as_windows(a,W)))

cummax = np.maximum.accumulate

def pp(a,w):

    N = a.size//w

    if a.size-w+1 > N*w:

        out = np.empty(a.size-w+1,a.dtype)

        out[:-1] = cummax(a[w*N-1::-1].reshape(N,w),axis=1).ravel()[:w-a.size-1:-1]

        out[-1] = a[w*N:].max()

    else:

        out = cummax(a[w*N-1::-1].reshape(N,w),axis=1).ravel()[:w-a.size-2:-1]

    out[1:N*w-w+1] = np.maximum(out[1:N*w-w+1],

                            cummax(a[w:w*N].reshape(N-1,w),axis=1).ravel())

    out[N*w-w+1:] = np.maximum(out[N*w-w+1:],cummax(a[N*w:]))

    return out

使用benchit包（很少有基准测试工具打包在一起；免责声明：我是它的作者）对建议的解决方案进行基准测试。

import benchit

funcs = [mapmax_strided, npmax_strided, numba1, numba2, scipy_max_filter1d, pp]

in_ = {(n,W):(np.random.randint(0,100,n),W) for n in 10**np.arange(2,6) for W in [2, 10, 20, 50, 100]}

t = benchit.timings(funcs, in_, multivar=True, input_name=['Array-length', 'Window-length'])

t.plot(logx=True, sp_ncols=1, save='timings.png')

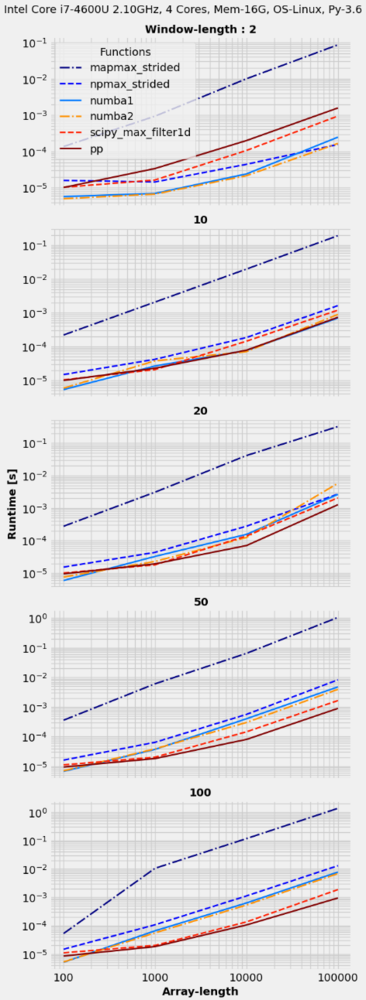
因此，numba 非常适合小于 的窗口大小10，此时没有明显的赢家，而在较大的窗口大小上，ppSciPy 则排名第二。

Answer 4

这是专门为较大窗户设计的方法。窗口大小为 O(1)，数据大小为 O(n)。

我已经完成了纯 numpy 和 pythran 实现。

我们如何在窗口大小上实现 O(1) ？我们使用“锯齿”技巧：如果 w 是窗口宽度，我们将数据分为很多 w ，对于每个组，我们从左到右和从右到左求累积最大值。任何中间窗口的元素分布在两组中，并且交集的最大值位于我们之前计算的累积最大值之中。因此，每个数据点总共需要 3 次比较。

benchit w=100；我的函数是 pp (numpy) 和 winmax (pythran)：

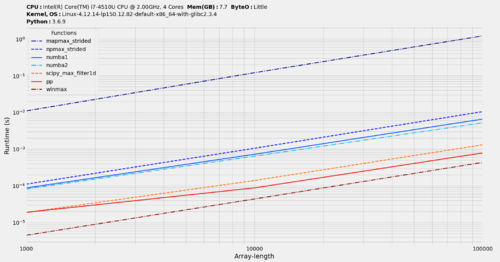
对于小窗口尺寸 w=5，图像更加均匀。有趣的是，即使对于非常小的尺寸，pythran 仍然具有巨大的优势。他们必须采取正确的措施来最大限度地减少呼叫开销。

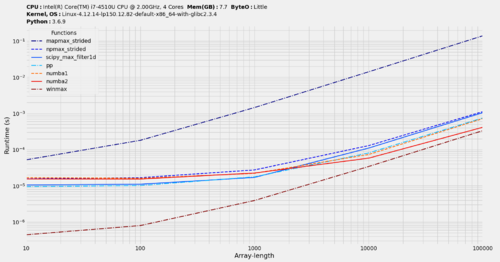
蟒蛇代码：

cummax = np.maximum.accumulate

def pp(a,w):

    N = a.size//w

    if a.size-w+1 > N*w:

        out = np.empty(a.size-w+1,a.dtype)

        out[:-1] = cummax(a[w*N-1::-1].reshape(N,w),axis=1).ravel()[:w-a.size-1:-1]

        out[-1] = a[w*N:].max()

    else:

        out = cummax(a[w*N-1::-1].reshape(N,w),axis=1).ravel()[:w-a.size-2:-1]

    out[1:N*w-w+1] = np.maximum(out[1:N*w-w+1],

                            cummax(a[w:w*N].reshape(N-1,w),axis=1).ravel())

    out[N*w-w+1:] = np.maximum(out[N*w-w+1:],cummax(a[N*w:]))

    return out

pythran 版本；编译用pythran -O3 <filename.py>; 这将创建一个可以导入的已编译模块：

import numpy as np

# pythran export winmax(float[:],int)

# pythran export winmax(int[:],int)

def winmax(data,winsz):

    N = data.size//winsz

    if N < 1:

        raise ValueError

    out = np.empty(data.size-winsz+1,data.dtype)

    nxt = winsz

    for j in range(winsz,data.size):

        if j == nxt:

            nxt += winsz

            out[j+1-winsz] = data[j]

        else:

            out[j+1-winsz] = out[j-winsz] if out[j-winsz]>data[j] else data[j]

    running = data[-winsz:N*winsz].max()

    nxt -= winsz << (nxt > data.size)

    for j in range(data.size-winsz,0,-1):

        if j == nxt:

            nxt -= winsz

            running = data[j-1]

        else:

            running = data[j] if data[j] > running else running

            out[j] = out[j] if out[j] > running else running

    out[0] = data[0] if data[0] > running else running

    return out

Answer 5

如果存在连续的n项目，则扩展解决方案需要循环：

np.maximum(*[A[i:len(A)-n+i+1] for i in range(n)])

为了避免这种情况，您可以使用跨步技巧并将其转换A为n-length 块的数组：

def rolling(a, window):

    shape = (a.size - window + 1, window)

    strides = (a.itemsize, a.itemsize)

    return np.lib.stride_tricks.as_strided(a, shape=shape, strides=strides)

例如：

>>> rolling(A, 3)

array([[ 8,  2,  8],

   [ 2,  8, 33],

   [ 8, 33, 33],

   [33, 33,  4]])

完成后你可以用 杀死它np.max(rolling(A, n), axis=1)。

尽管它很优雅，但这个解决方案和第一个解决方案都不是高效的，因为我们在仅相差两项的相邻块上重复应用最大值。

Answer 6

对于所有 n 的递归解决方案

import numpy as np

import sys

def recursive(a: np.ndarray, n: int, b=None, level=2):

    if n <= 0 or n > len(a):

        raise ValueError(f'len(a):{len(a)} n:{n}')

    if n == 1:

        return a

    if len(a) == n:

        return np.max(a)

    b = np.maximum(a[:-1], a[1:]) if b is None else np.maximum(a[level - 1:], b)

    if n == level:

        return b

    return recursive(a, n, b[:-1], level + 1)

test_data = np.array([8, 2, 33, 4, 3, 6])

for test_n in range(1, len(test_data) + 2):

    try:

        print(recursive(test_data, n=test_n))

    except ValueError as e:

        sys.stderr.write(str(e))

输出

[ 8  2 33  4  3  6]

[ 8 33 33  4  6]

[33 33 33  6]

[33 33 33]

[33 33]

33

len(a):6 n:7

关于递归函数

你可以观察下面的数据，然后你就会知道如何写递归函数了。

"""

np.array([8, 2, 33, 4, 3, 6])

n=2: (8, 2),     (2, 33),    (33, 4),    (4, 3),   (3, 6)  => [8, 33, 33, 4, 6] => B' = [8, 33, 33, 4]

n=3: (8, 2, 33), (2, 33, 4), (33, 4, 3), (4, 3, 6)         => B' [33, 4, 3, 6]  =>  np.maximum([8, 33, 33, 4], [33, 4, 3, 6]) => 33, 33, 33, 6

...

"""