值在 -1 到 1 之间并且总和为 1 的随机 numpy 数组

Question

x创建给定值的NumPy 数组的最佳方法是什么，其size值随机（且均匀？）分布在-1和之间1，并且总和也为1？我尝试2*np.random.rand(size)-1并np.random.uniform(-1,1,size)基于这里的讨论，但是如果我采用转换方法，通过之后按它们的总和重新缩放这两种方法，x/=np.sum(x)这可以确保元素总和为 1，但是：数组中的某些元素突然变得更大或小于 1 (> 1, < -1)，这是不需要的。

Answer 1

您可以为正值和负值创建两个不同的数组。确保正侧加起来为 1，负侧加起来为 0。

import numpy as np

size = 10

x_pos = np.random.uniform(0, 1, int(np.floor(size/2)))

x_pos = x_pos/x_pos.sum() 

x_neg = np.random.uniform(0, 1, int(np.ceil(size/2)))

x_neg = x_neg - x_neg.mean()

x = np.concatenate([x_pos, x_neg])

np.random.shuffle(x)

print(x.sum(), x.max(), x.min())

>>> 0.9999999999999998 0.4928358768227867 -0.3265210342316333

print(x)

>>>[ 0.49283588  0.33974127 -0.26079784  0.28127281  0.23749531 -0.32652103

  0.12651658  0.01497403 -0.03823131  0.13271431]

Answer 2

在这种情况下，让我们让均匀分布开始该过程，但调整值以使总和为 1。为了便于说明，我将使用初始步骤这给我们总和为 -0.5，但我们需要[-1, -0.75, 0, 0.25, 1] 1.0

第 1 步：计算所需的总找零金额：1.0 - (-0.5) = 1.5。

现在，我们将分配元素之间的变化是某种适当的方式。我使用的一种简单方法是最大程度地移动中间元素，同时保持端点稳定。

步骤 2：计算每个元素与较近端点的差异。对于您的不错的范围，这是1 - abs(x)

第 3 步：总结这些差异。分成所需的变化。这给出了调整每个元素的量。

将这些内容放入图表中：

  x    diff  adjust

-1.0   0.00  0.0

-0.75  0.25  0.1875

 0.0   1.0   0.75

 0.25  0.75  0.5625

 1.0   0.0   0.0

现在，只需添加x和adjust列即可获取新值：

 x    adjust  new

-1.0  0.0     -1.0

-0.75 0.1875  -0.5625

 0    0.75     0.75

 0.25 0.5625   0.8125

 1.0  0.0      1.0

这是您调整后的数据集：总和为 1.0，端点完好无损。

简单的Python代码：

x = [-1, -0.75, 0, 0.25, 1.0]

total = sum(x)

diff = [1 - abs(q) for q in x]

total_diff = sum(diff)

needed = 1.0 - sum(x)

adjust = [q * needed / total_diff for q in diff]

new = [x[i] + adjust[i] for i in range(len(x))]

for i in range(len(x)):

    print(f'{x[i]:8} {diff[i]:8} {adjust[i]:8} {new[i]:8}')

print (new, sum(new))

输出：

      -1        0      0.0     -1.0

   -0.75     0.25   0.1875  -0.5625

       0        1     0.75     0.75

    0.25     0.75   0.5625   0.8125

     1.0      0.0      0.0      1.0

[-1.0, -0.5625, 0.75, 0.8125, 1.0] 1.0

我会让你在 NumPy 中对其进行向量化。

Answer 3

拒绝抽样

您可以使用拒绝抽样。下面的方法通过在比原始空间小 1 维的空间中进行采样来实现此目的。

• 第 1 步：通过从均匀分布中对每个 x(i) 进行采样来随机采样 x(1)、x(2)、...、x(n-1)

• 步骤 2：如果总和 S = x(1) + x(2) + ... + x(n-1) 低于 0 或高于 2，则拒绝并重新开始步骤 1。

• 步骤 3：计算第 n 个变量 x(n) = 1-S

---

直觉

您可以在笛卡尔坐标 ±1、±1、.. 的 n 维立方体内部查看向量 x(1)、x(2)、...、x(n-1)、x(n)。 . , ±1. 这样您就遵循约束 -1 <= x(i) <= 1。

坐标之和必须等于 1 的附加约束将坐标限制到比超立方体更小的空间，并且将是维度为n-1 的超平面。

如果您定期进行拒绝采样，即从所有坐标的均匀分布中采样，那么您将永远不会遇到约束。采样点永远不会在超平面内。因此，您考虑 n-1 个坐标的子空间。现在您可以使用拒绝采样。

视觉上

假设您的维度为 4，那么您可以绘制 4 的坐标中的 3。该图（均匀地）填充了一个多面体。下面通过以切片形式绘制多面体来说明这一点。每个切片对应于不同的总和 S = x(1) + x(2) + ... + x(n-1) 以及不同的 x(n) 值。

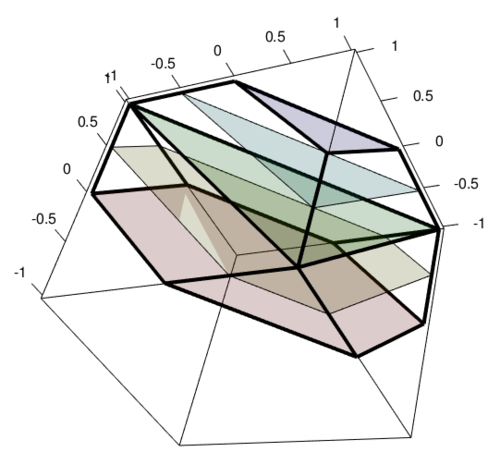
图像：3 个坐标的域。每个彩色表面都与第四个坐标的不同值相关。

边际分布

对于大维度，拒绝采样的效率将变得较低，因为拒绝的比例随着维度的数量而增长。

“解决”这个问题的一种方法是从边际分布中抽样。然而，计算这些边际分布有点乏味。比较：对于从狄利克雷分布生成样本，存在类似的算法，但在这种情况下，边际分布相对容易。（但是，导出这些分布也不是不可能，请参见下文“与欧文霍尔分布的关系”）

在上面的示例中，x(4) 坐标的边缘分布对应于切口的表面积。因此，对于 4 维，您可能能够根据该数字计算出计算结果（您需要计算这些不规则多边形的面积），但对于更大的维度，它开始变得更加复杂。

与欧文·霍尔分布的关系

要获得边际分布，您可以使用截断的欧文霍尔分布。欧文霍尔分布是均匀分布变量之和的分布，并且遵循某些分段多项式形状。下面通过一个示例对此进行了演示。

代码

由于我的 python 生锈了，所以我主要添加 R 代码。该算法非常基础，因此我想任何 Python 编码人员都可以轻松地将其改编为 Python 代码。在我看来，这个问题的困难部分更多地是关于算法，而不是关于如何用 Python 编码（尽管我不是 Python 编码员，所以我把这个问题留给其他人）。

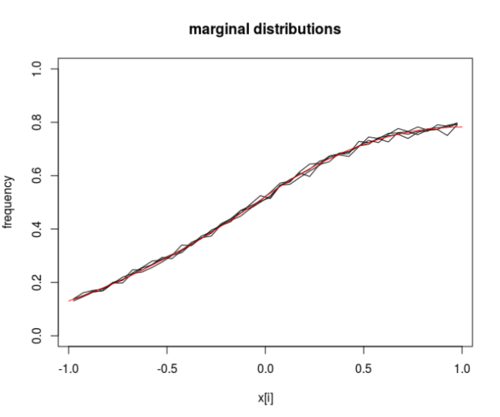
图像：采样的输出。4 条黑色曲线是四个坐标的边缘分布。红色曲线是基于欧文霍尔分布的计算。这可以扩展到通过直接计算而不是拒绝采样的采样方法。

python中的拒绝采样

import numpy as np

def sampler(size):

   reject = 1

   while reject:

      x = np.random.rand(size - 1) # step 1

      S = np.sum(x)

      reject = (S<0) or (S>2)      # step 2

   x = np.append(x,1-S)            # step 3

   return[x]

y = sampler(5) 

print(y, np.sum(y))

R 中的更多代码，包括与 Irwin Hall 分布的比较。该分布可用于计算边际分布，并可用于设计一种比拒绝采样更有效的算法。

### function to do rejection sample

samp <- function(n) {

  S <- -1

  ## a while loop that performs step 1 (sample) and 2 (compare sum)

  while((S<0) || (S>2) ) { 

    x <- runif(n-1,-1,1)

    S <- sum(x)

  }

  x <- c(x,1-S) ## step 3 (generate n-th coordinate)

  x

}

### compute 10^5 samples

y <- replicate(10^5,samp(4))

### plot histograms

h1 <- hist(y[1,], breaks = seq(-1,1,0.05))

h2 <- hist(y[2,], breaks = seq(-1,1,0.05))

h3 <- hist(y[3,], breaks = seq(-1,1,0.05))

h4 <- hist(y[4,], breaks = seq(-1,1,0.05))

### histograms together in a line plot

plot(h1$mids,h1$density, type = 'l', ylim = c(0,1),

     xlab = "x[i]", ylab = "frequency", main = "marginal distributions")

lines(h2$mids,h2$density)

lines(h3$mids,h3$density)

lines(h4$mids,h4$density)

### add distribution based on Irwin Hall distribution

### Irwin Hall PDF

dih <- function(x,n=3) {

  k <- 0:(floor(x))   

  terms <- (-1)^k * choose(n,k) *(x-k)^(n-1)

  sum(terms)/prod(1:(n-1))

}

dih <- Vectorize(dih)

### Irwin Hall CDF

pih <- function(x,n=3) {

  k <- 0:(floor(x))   

  terms <- (-1)^k * choose(n,k) *(x-k)^n

  sum(terms)/prod(1:(n))

}

pih <- Vectorize(pih)

### adding the line 

### (note we need to scale the variable for the Erwin Hall distribution)

xn <- seq(-1,1,0.001)

range <- c(-1,1)

cum <- pih(1.5+(1-range)/2,3)

scale <- 0.5/(cum[1]-cum[2]) ### renormalize

                           ### (the factor 0.5 is due to the scale difference)

lines(xn,scale*dih(1.5+(1-xn)/2,3),col = 2)

Answer 4

您已经编写了代数矛盾的代码。您引用的问题的假设是随机样本将大约填充范围 [-1, 1]。如果线性重新缩放，从代数角度来说不可能维持该范围，除非在缩放之前总和为 1 ，这样缩放不会发生任何变化。

您在这里有两个直接选择：

1. 放弃范围的想法。进行简单的更改以确保总和至少为1，并在缩放后接受更小的范围。你可以用任何你喜欢的方式来做到这一点，使选择偏向积极的一面。

2. 更改原始的“随机”选择算法，使其总和趋于接近 1，然后添加一个最终元素，使其恰好返回 1.0。那么你就不必重新缩放。

---

考虑基本的区间代数。如果您以 的间隔（范围）开始[-1,1]并乘以a（这适合1/sum(x)您），则所得间隔为[-a,a]。如果a > 1，就像您的情况一样，所得的间隔更大。如果a < 0，则交换区间的两端。

---

从您的评论中，我推断您的概念问题更加微妙。您试图强制预期值为 的分布0产生总和为 1 的分布。这是不现实的，除非您同意以某种方式在没有特定界限的情况下扭曲该分布。到目前为止，你拒绝了我的建议，但还没有提出任何你愿意接受的建议。在您确定这一点之前，我无法合理地为您建议解决方案。