有什么方法可以在 python 中使用 scikit-learn 预测每月的时间序列？

Question

我想product' sales_index通过使用每月时间序列中的多个功能进行预测。一开始，我开始使用ARMA,ARIMA来执行此操作，但输出对我来说不是很令人满意。在我的尝试中，我只是使用dates和sales列进行预测，输出对我来说并不现实。我想我应该包括更多的特征列来预测sales_index列。但是，我想知道是否有任何方法可以通过使用每月时间序列中的多个特征来进行此预测。我没有使用scikit-learn. 谁能指出我这样做的任何可能方法？任何可能的想法？我尝试使用 ARMA/ARIMA：这是关于这个要点的可重现的月度时间序列数据，这是我目前的尝试：import pandas as pdfrom statsmodels.tsa.arima_model import ARMAfrom statsmodels.tsa.arima_model import ARIMAfrom statsmodels.tsa.statespace.sarimax import SARIMAXimport matplotlib.pyplot as pltdf = pd.read_csv("tsdf.csv", sep=",")dates = pd.date_range(start='2015-01', freq='MS', periods=len(df))df.set_index(dates,inplace=True)train = df[df.index < '2019-01']test = df[df.index >= '2019-01']model = ARMA(train['sales_index'],order=(2,0))model_fit = model.fit()predictions = model_fit.predict(start=len(train), end=len(train)+len(test)-1, dynamic=False)# plot resultsplt.figure(figsize=(12,6))plt.plot(test['sales_index'])plt.plot(predictions, color='red')plt.show()这是我当前尝试的输出：在我的尝试中，我只是简单地使用df['sales_index]anddf['dates']作为ARMA模型。显然这样做，预测输出不是很真实和信息丰富。我在想是否有任何方法可以将所有功能列提供给df['sales_index']模型进行预测df['sales_index']。我想不出用ARMA模型做这件事的更好方法。也许scikit-learn可以为这个预测提供更好的作用。我不确定如何使用sklearn此时间序列分析来实现此目的。谁能指出sklearn这个时间序列的可能解决方案？有没有可能这样做sklearn？任何可能的想法？谢谢

Answer 1

概述

通过使用Scikit-Learn库，可以考虑使用不同的决策树来预测数据。在此示例中，我们将使用AdaBoostRegressor，但也可以切换到RandomForestRegressor或任何其他可用的树。因此，通过选择树，我们应该意识到去除数据的趋势，通过这种方式，我们说明了通过分别对数据进行差分和对数变换来控制时间序列的均值和方差的示例。

准备数据

时间序列有两个基本组成部分，即均值和方差。理想情况下，我们希望控制这些组件，对于可变性，我们可以简单地对数据应用对数变换，对于趋势我们可以区分它，我们稍后会看到。

此外，对于这种方法，我们考虑实际值 y_t 可以用两个先验值 y_t-1 和 y_t-2 来解释。您可以通过修改函数的输入来处理这些滞后值range。

# Load data

tsdf = pd.read_csv('tsdf.csv', sep="\t")

# For simplicity I just take the target variable and the date

tsdf = tsdf[['sales_index', 'dates']]

# Log value

tsdf['log_sales_index'] = np.log(tsdf.sales_index)

# Add previous n-values

for i in range(3):

    

    tsdf[f'sales_index_lag_{i+1}'] = tsdf.sales_index.shift(i+1)

    

    # For simplicity we drop the null values 

    tsdf.dropna(inplace=True)

    

    tsdf[f'log_sales_index_lag_{i+1}'] = np.log(tsdf[f'sales_index_lag_{i+1}'])

    

    tsdf[f'log_difference_{i+1}'] = tsdf.log_sales_index - tsdf[f'log_sales_index_lag_{i+1}']

一旦我们的数据准备就绪，我们就会得到类似于下图的结果。

数据是固定的吗？

为了控制时间序列的平均分量，我们应该对数据进行一些差分。为了确定是否需要执行此步骤，我们可以执行单位根测试。为简单起见，我们将考虑 KPSS 检验，我们假设数据是平稳的零假设，特别是，它假设围绕均值或线性趋势平稳。

from arch.unitroot import KPSS

# Test for stationary

kpss_test = KPSS(tsdf.sales_index)

# Test summary 

print(kpss_test.summary().as_text())

我们看到P-value = .280大于通常的约定0.05。因此，我们需要对数据应用一阶差分。作为旁注，可以迭代地执行此测试以了解应将多少差异应用于数据。

在下图中，我们看到了原始数据与对数一阶差分的比较，注意时间序列的这些最后值突然发生变化，这似乎是结构性变化，但我们不会深入潜入其中。如果您想深入了解这个主题，布鲁斯·汉森 (Bruce Hansen) 提供的这些幻灯片很有用。

plt.figure(figsize=(12, 6))
plt.subplot(1,2,1)
plt.plot(tsdf.sales_index)
plt.title('Original Time Series')
plt.subplot(1,2,2)
plt.plot(tsdf.log_difference_1)
plt.title('Log first difference Time Series')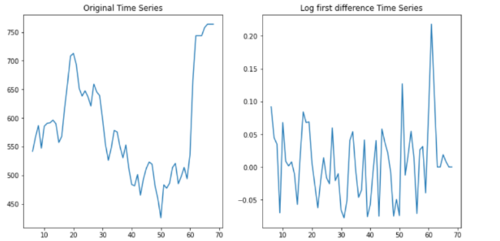

决策树模型

正如我们之前所说，我们正在考虑决策树模型，在使用它们时应该注意从时间序列中删除趋势。例如，如果你有上升趋势，tress 不擅长预测下降趋势。在下面的代码示例中，我选择了AdaBoostRegressor，但您可以自由选择其他树模型。另外，注意 被 log_difference_1认为是由log_difference_2和解释的log_difference_3。

注意。您的数据集还有其他协变量 或aus_avg_rain，slg_adt_ctl因此考虑将它们用于预测，您也可以对它们应用滞后值。

from sklearn.model_selection import train_test_split

from sklearn.ensemble import AdaBoostRegressor

# Forecast difference of log values

X, Y = tsdf[['log_difference_2', 'log_difference_3']], tsdf['log_difference_1']

# Split in train-test

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, shuffle=False, random_state=0)

# Initialize the estimator

mdl_adaboost = AdaBoostRegressor(n_estimators=500, learning_rate=0.05)

# Fit the data

mdl_adaboost.fit(X_train, Y_train)

# Make predictions

pred = mdl_adaboost.predict(X_test)

test_size = X_test.shape[0]

评估预测

test_size = X_test.shape[0]

plt.plot(list(range(test_size)), np.exp(tsdf.tail(test_size).log_sales_index_lag_1  + pred), label='predicted', color='red')

plt.plot(list(range(test_size)), tsdf.tail(test_size).sales_index, label='real', color='blue')

plt.legend(loc='best')

plt.title('Predicted vs Real with log difference values')

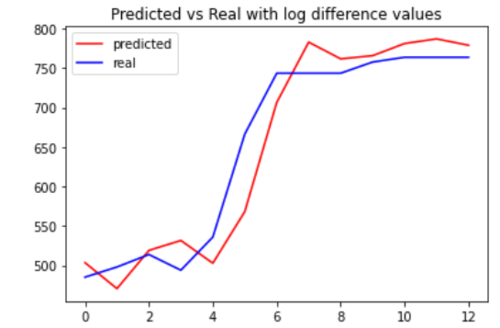
决策树模型似乎准确地预测了真实值。我将使用TimeSeriesSplitfrom 函数scikit-learn通过平均绝对误差来评估模型的误差。

from sklearn.model_selection import TimeSeriesSplit

from sklearn.metrics import mean_absolute_error

X, Y = np.array(tsdf[['log_difference_2', 'log_difference_3']]), np.array(tsdf['log_difference_1'])

# Initialize a TimeSeriesSplitter

tscv = TimeSeriesSplit(n_splits=5)

# Retrieve log_sales_index and sales_index to unstransform data

tsdf_log_sales_index = np.array(tsdf.copy().reset_index().log_sales_index_lag_1)

tsdf_sales_index = np.array(tsdf.copy().reset_index().sales_index_lag_1)

# Dict to store metric value at every iteration

metric_iter = {}

for idx, val in enumerate(tscv.split(X)):

    

        train_i, test_i = val

    

        X_train, X_test = X[train_i], X[test_i]

        Y_train, Y_test = Y[train_i], Y[test_i]

        # Initialize the estimator

        mdl_adaboost = AdaBoostRegressor(n_estimators=500, learning_rate=0.05)

        # Fit the data

        mdl_adaboost.fit(X_train, Y_train)

        # Make predictions

        pred = mdl_adaboost.predict(X_test)

        

        # Unstransform predictions

        pred_untransform = [np.exp(val_test + val_pred) for val_test, val_pred in zip(tsdf_log_sales_index[test_i], pred)]

        

        # Real value

        real = tsdf_sales_index[test_i]

        

        # Store metric

        metric_iter[f'iter_{idx + 1}'] = mean_absolute_error(real, pred_untransform)             

现在我们看到平均MAE误差非常低。

print(f'Average MAE error: {np.mean(list(metric_iter.values()))}')

>>> Average MAE error: 17.631090959806535

Answer 2

这有两个部分：

1. 一个有效的预测代码解决方案。

2. 几个话题的简单讨论

解决方案

我将建议一种略有不同且更抽象的方法：使用构建在 scikit-learn 之上的Darts 。它包括您期望的“列表”库（例如，pandas 和 NumPy），但也包括一些您需要对该领域有相当深入的了解才能考虑包含的库（例如，Torch、Prophet 和 Holidays）。此外，它已经包含了许多模型。重要说明：特定库是 u8darts，而不是飞镖。它们很相似——并且具有相似的依赖关系——但它们并不相同。

使用它，您可以轻松地开发出具有相当不错结果的预测模型。例如，整个代码，包括合并重命名的列标题（以及删除未重命名的列和重复的行）只是几行。

import pandas as pd

import matplotlib.pyplot as plt

from darts import TimeSeries

from darts.models import ExponentialSmoothing

df = pd.read_csv("../data/tsdf.csv", sep="\t")

df.drop(['Unnamed: 0', 'aus_slg_fmCatl'], axis=1, inplace = True)

df.columns = ['Date', 'adult_cattle(head)','Bulls Bullocks & Steers(head)', 'Cows&Heifers(head)',

              'Calves(head)', 'Beef(tonnes)', 'Veal(tonnes)','Adult cattle(kg/head)', 'Calves(kg/head)',

              'aust-avg_rain','US/AUS_ExchangeRate', 'sales_index', 'retail_sales_index']

df.drop_duplicates(subset=['Date'], inplace=True)

series = TimeSeries.from_dataframe(df, 'Date', 'Beef(tonnes)').values

train, val = series.split_before(pd.Timestamp('2019-01-01'))

model = ExponentialSmoothing()

model.fit(train)

prediction = model.predict(len(val))

series.plot(label='actual')

prediction.plot(label='forecast', lw=2)

plt.legend()

此外，他们的 repo 有一个带有额外模型和示例的笔记本

结果

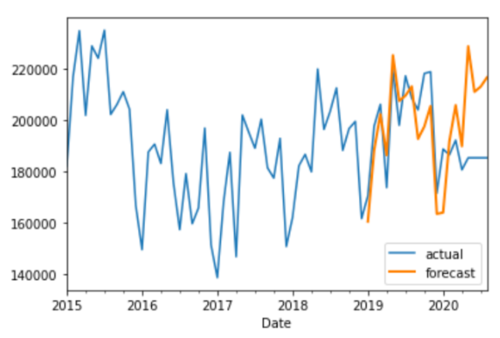
讨论

针对我们收到的评论中的讨论，我认为有几点需要说明。

去除季节性

如果您正在为预测模型拍摄，这是您很少想做的事情。如果你知道每年冬天家庭/办公室供暖的燃料价格都会上涨，但决定将其排除在外——你会被交易员活活吃掉，他们很乐意拿走你的钱。

虚拟数据

这里的诀窍是您不知道您的虚拟数据是否与真实数据看起来足够相似。然而，解决方案是一个不同的问题。

“在 Python 中使用 R 库……”

ARMA 和 ARIMA

...不太可能产生丰硕的结果，部分原因是误差项假设误差是IID，但市场存在偏差。指数平滑效果很好，因为它替代了

“但是当我针对 sales_index 运行它时……”

sales_index 将由几个自变量组成。正如您所期望的那样，肉类生产（奇怪的是与降雨量呈负相关）和汇率。但是，您的模型中未包含其他国家/地区的生产数据（100% 纯有机、草料、“AAA”艾伯塔牛肉）、税收、国内牛肉生产、运输等。这就是您可能不想要的原因对抗既有宽客又有专业领域专业知识的专业交易员。最后，我要指出的是，时间上没有任何迹象表明这是正常的还是不正常的。

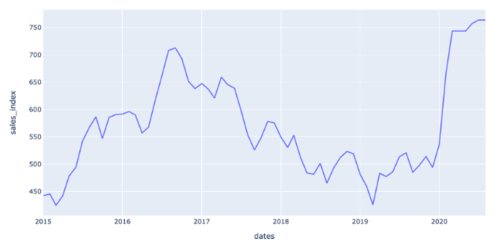
从 2015 年到 2017 年，似乎出现了 1.5 年的上升，随后一直下降到 2019 年。这似乎在重复，但 2020 年的突然变化让人相信这是一种失常。但数据太小，很难判断任何有效性。在这种情况下，趋势线或通道会更好。

Answer 3

在初始化模型和进行预测时，您可以ARMA使用可选参数向模型添加其他功能。exog

例如，要添加一些您的功能：

# initialize the model

model = ARMA(train['sales_index'], 

             exog=train[['slg_adt_ctl', 'slg_bbs', 'retail_sales_index']],

             order=(2,0))

model_fit = model.fit() # fit the model

# make predictions

predictions = model_fit.predict(start=len(train), 

                                end=len(train)+len(test)-1, 

                                exog=test[['slg_adt_ctl', 'slg_bbs', 'retail_sales_index']], 

                                dynamic=False)

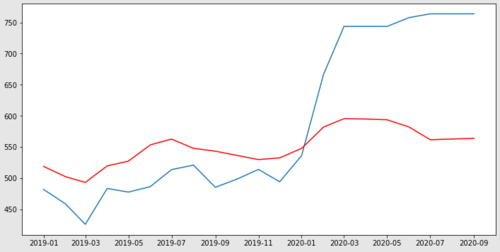
当我们制作预测图时，我们现在获得了一些额外的预测能力。