移动点和移动线段的碰撞位置和时间（连续碰撞检测）

Question

我正在研究一个 2D 对撞机系统，该系统将形状分解为一个可能的基元：由两点定义的不可穿透的部分。为了为该系统提供碰撞检测，我使用了一种静态碰撞检测方法，该方法每帧计算一次线段的边缘与当前处理的线段之间的距离（点/线距离）。如果距离太小，则在该帧期间触发碰撞。这工作正常，但如果一个或多个物体表现出高速，则会出现已知的隧道问题。所以我正在修补替代品。现在我想介绍在动态点/动态段上运行的连续碰撞检测（CCD）。我的问题是：我不知道怎么做。我知道如何在两个移动点、移动点和静态段之间进行连续碰撞，但不知道如何在移动点（由点 P 定义）和移动段（由点 U 和 V 定义，两者都可以）之间进行 CCD完全自由移动）。但没有提出这些确切的要求：点和线段都在移动段可以旋转和拉伸（因为 U 和 V 可以自由移动）需要准确找到两帧之间的碰撞时间和碰撞点（CCD，无静态碰撞测试）如果可能的话，我更喜欢数学上完美的解决方案（没有迭代近似算法，扫描体积）注意：扫掠线形状并不总是凸多边形，因为 U、V 点的自由度注意：测试与扫描体积的碰撞测试是不准确的，因为与多边形的碰撞点并不意味着实际运动中的碰撞点（参见图像，一旦实际段穿过轨迹，该点将离开多边形点）到目前为止，我想出了以下方法，给出：sP（帧开始时的 P），eP（帧末尾的 P），sU（帧开始处的 U），eU（帧末尾的 U），sV（帧开始时的 V），eV（帧末尾的 V）问题：它们会碰撞吗？如果是，何时何地？解决方案：将帧中每个点的时间轨迹建模为线性运动（0 <= t <= 1的线轨迹）P(t) = sP * (1 - t) + eP * tU(t) = sU * (1 - t) + eU * tV(t) = sV * (1 - t) + eV * t（0 <= a <= 1表示由 U 和 V 定义的线段上的位置）：UV(a, t) = U(t) * (1 - a) + V(t) * a通过使点和线段方程相等来模拟碰撞：P(t) = UV(a, t)P(t) = U(t) * (1 - a) + V(t) * a为从点 P 到线段上的点的向量导出一个函数：F(a, t) = P(t) - (1 - a) * U(t) - a * V(t)现在要找到碰撞，需要找到a和t，以便F(a, t) = (0, 0)和[0, 1] 中的 a,t。这可以建模为具有 2 个变量的寻根问题。将时间轨迹方程插入F(a, t)中：F(a, t) = (sP * (1 - t) + eP * t) - (1 - a) * (sU * (1 - t) + eU * t) - a * (sV * (1 - t ) + eV * t)按维度（x 和 y）分离时间轨迹方程：Fx(a, t) = (sP.x * (1 - t) + eP.x * t) - (1 - a) * (sU.x * (1 - t) + eU.x * t) - a * (sV.x * (1 - t) + eV.x * t)Fy(a, t) = (sP.y * (1 - t) + eP.y * t) - (1 - a) * (sU.y * (1 - t) + eU.y * t) - a * (sV.y * (1 - t) + eV.y * t)现在我们有两个方程和两个要求解的变量（分别为Fx、Fy和a、t），因此我们应该能够使用求解器来获得a和t，然后检查它们是否位于 [0, 1]..对吗？

Answer 1

TLDR

我确实读过“……大约 5 分钟来评估……”

没办法太长，这是一个针对许多线和点的实时解决方案。

抱歉，这不是一个完整的答案（我没有合理化和简化方程式），它将找到我留给你的截距点。

我还可以看到解决方案的几种方法，因为它围绕一个三角形（见图）旋转，当平面是解决方案时。下面的方法找到三角形的长边等于短边之和的时间点。

求解你（时间）

这可以作为一个简单的二次方程来完成，其系数从 3 个起点导出，每个点的单位时间向量。为你解决

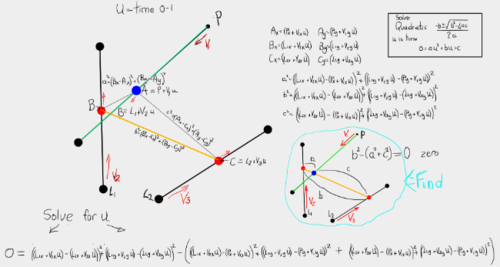
下图提供了更多详细信息。

• 点P是点的起始pos

• 点L1、L2是线端的起点。

• 矢量V1是单位时间内（沿绿线）的点。

• 矢量V2、V3用于单位时间内的线路末端。

• u是单位时间

• A是点（蓝色），B和C是线端点（红色）

存在（可能）一个时间点u，其中A在B和C线上。此时，线AB（作为a）和AC（作为c）的长度总和等于线BC（作为b）（橙色线）的长度。

这意味着当b - (a + c) == 0时，该点在线上。在图像中，点被平方，因为这稍微简化了它。b ² - (a ² + c ² ) == 0

图像底部是根据u, P, L1, L2, V1, V2, V3 的方程（二次） 。

该等式需要重新排列，以便得到(???)u ² + (???)u + (???) = 0

抱歉，手动执行此操作非常乏味且很容易出错。我手头没有工具，也不使用 python，所以我不知道你使用的数学库。但是它应该能够帮助您找到如何计算(???)u ² + (???)u + (???) = 0 的系数

更新

忽略上面的大部分内容，因为我犯了一个错误。b - (a + c) == 0与b 2 - (a 2 + c 2 ) == 0不同。第一个是需要的，这是处理部首时的一个问题（请注意，仍然可以使用 虚数a + bi == sqrt(a^2 + b^2)在哪里的解决方案）。i

另一种解决方案

所以我探索了其他选择。

最简单的有一个小缺陷。它将返回拦截时间。但是，必须对其进行验证，因为它还会在拦截线时返回拦截时间，而不是线段BC

因此，当找到结果时，您可以通过将找到的点和线段的点积除以线段长度的平方来测试它。isPointOnLine请参阅测试片段中的功能。

为了解决这个问题，我使用了这样一个事实，即当点在线上时，线BC与从B到A的向量的叉积将为 0。

一些重命名

使用上图，我重命名了变量，这样我就可以更轻松地完成所有繁琐的工作。

/*

point P is  {a,b}

point L1 is  {c,d}

point L2 is  {e,f}

vector V1 is {g,h}

vector V2 is {i,j}

vector V3 is {k,l}

Thus for points A,B,C over time u    */

Ax = (a+g*u)

Ay = (b+h*u)

Bx = (c+i*u)

By = (d+j*u)

Cx = (e+k*u)

Cy = (f+l*u)

/* Vectors BA and BC at u */

Vbax = ((a+g*u)-(c+i*u))

Vbay = ((b+h*u)-(d+j*u))

Vbcx = ((e+k*u)-(c+i*u))

Vbcy = ((f+l*u)-(d+j*u))

/*

   thus Vbax * Vbcy - Vbay * Vbcx == 0 at intercept 

*/

这给出了二次

0 = ((a+g*u)-(c+i*u)) * ((f+l*u)-(d+j*u)) - ((b+h*u)-(d+j*u)) * ((e+k*u)-(c+i*u))

重新排列我们得到

0 = -((i*l)-(h*k)+g*l+i*h+(i+k)*j-(g+i)*j)*u* u -(d*g-c*l-k*b-h*e+l*a+g*f+i*b+c*h+(i+k)*d+(c+e)*j-((f+d)*i)-((a+c)*j))*u +(c+e)*d-((a+c)*d)+a*f-(c*f)-(b*e)+c*b

因此系数是

 A = -((i*l)-(h*k)+g*l+i*h+(i+k)*j-(g+i)*j)

 B = -(d*g-c*l-k*b-h*e+l*a+g*f+i*b+c*h+(i+k)*d+(c+e)*j-((f+d)*i)-((a+c)*j))

 C = (c+e)*d-((a+c)*d)+a*f-(c*f)-(b*e)+c*b

我们可以使用二次公式求解（见右上图）。

请注意，可能有两种解决方案。在示例中，我忽略了第二个解决方案。但是，由于第一个可能不在线段上，如果在0 <= u <= 1范围内，您需要保留第二个解决方案，以防第一个失败。您还需要验证该结果。

测试

为了避免错误，我不得不测试解决方案

下面是一个片段，它生成随机的随机线对，然后生成随机线，直到找到截距。

感兴趣的功能是

• movingLineVPoint如果有的话，它返回第一次拦截的单位时间。

• isPointOnLine来验证结果。

const ctx = canvas.getContext("2d");

canvas.addEventListener("click",test);

const W = 256, H = W, D = (W ** 2 * 2) ** 0.5;

canvas.width  = W; canvas.height = H;

const rand = (m, M) => Math.random() * (M - m) + m;

const Tests = 300;

var line1, line2, path, count = 0; 

setTimeout(test, 0);

// creating P point L line

const P = (x,y) => ({x,y,get arr() {return [this.x, this.y]}}); 

const L = (l1, l2) => ({l1,l2,vec: P(l2.x - l1.x, l2.y - l1.y), get arr() {return [this.l1, this.l2]}}); 

const randLine = () => L(P(rand(0, W), rand(0, H)), P(rand(0, W), rand(0, H)));

const isPointOnLine = (p, l) =>  {

    const x = p.x - l.l1.x;

    const y = p.y - l.l1.y;

    const u = (l.vec.x * x + l.vec.y * y) / (l.vec.x * l.vec.x + l.vec.y * l.vec.y);

    return u >= 0 && u <= 1;

}

// See answer illustration for names

// arguments in order Px,Py,L1x,l1y,l2x,l2y,V1x,V1y,V2x,V2y,V3x,V3y

function movingLineVPoint(a,b, c,d, e,f, g,h, i,j, k,l) {

    var A = -(i*l)-(h*k)+g*l+i*h+(i+k)*j-(g+i)*j;

    var B = -d*g-c*l-k*b-h*e+l*a+g*f+i*b+c*h+(i+k)*d+(c+e)*j-((f+d)*i)-((a+c)*j)

    var C = +(c+e)*d-((a+c)*d)+a*f-(c*f)-(b*e)+c*b

    // Find roots if any. Could be up to 2

    // Using the smallest root >= 0 and <= 1

    var u, D, u1, u2;

    // if A is tiny we can ignore

    if (Math.abs(A) < 1e-6) { 

        if (B !== 0) {

            u = -C / B;

            if (u < 0 || u > 1) { return }  // !!!!  no solution  !!!!

        } else { return }                   // !!!!  no solution  !!!!

    } else {

        B /= A;

        D = B * B - 4 * (C / A);

        if (D > 0) {

            D **= 0.5;

            u1 = 0.5 * (-B + D);

            u2 = 0.5 * (-B - D);

            if ((u1 < 0 || u1 > 1) && (u2 < 0 || u2 > 1))  { return }  // !!!!  no solution  !!!!

            if (u1 < 0 || u1 > 1) { u = u2 }        // is first out of range

            else if (u2 < 0 || u2 > 1) { u = u1 }   // is second out of range

            else if (u1 < u2) { u = u1 }            // first is smallest

            else { u = u2 }

        } else if (D === 0) {

            u = 0.5 * -B;

            if (u < 0 || u > 1)  { return }  // !!!!  no solution  !!!!            

        } else { return }                    // !!!!  no solution  !!!! 

    }    

    return u;

}

function test() {

   if (count> 0) { return }

   line1 = randLine();

   line2 = randLine();

   count = Tests

   subTest();

}

function subTest() {

   path = randLine()

   ctx.clearRect(0,0,W,H);

   drawLines();

   const u = movingLineVPoint(

       path.l1.x, path.l1.y,

       line1.l1.x, line1.l1.y,

       line2.l1.x, line2.l1.y,

       path.vec.x, path.vec.y,

       line1.vec.x, line1.vec.y,

       line2.vec.x, line2.vec.y

   );

   

   if (u !== undefined) { // intercept found maybe

      pointAt = P(path.l1.x + path.vec.x * u, path.l1.y + path.vec.y * u);

      lineAt = L(

          P(line1.l1.x + line1.vec.x * u, line1.l1.y + line1.vec.y * u),

          P(line2.l1.x + line2.vec.x * u, line2.l1.y + line2.vec.y * u)

      );

      const isOn = isPointOnLine(pointAt, lineAt);

      if (isOn) {

          drawResult(pointAt, lineAt);

          count = 0;

          info.textContent = "Found at: u= " + u.toFixed(4) + ". Click for another";

          return;

      }

   }

   setTimeout((--count < 0 ? test : subTest), 18);

}   

function drawLine(line, col = "#000", lw = 1) {

    ctx.lineWidth = lw;

    ctx.strokeStyle = col;

    ctx.beginPath();

    ctx.lineTo(...line.l1.arr);

    ctx.lineTo(...line.l2.arr);

    ctx.stroke();

}

function markPoint(p, size = 3, col = "#000", lw = 1) {

    ctx.lineWidth = lw;

    ctx.strokeStyle = col;

    ctx.beginPath();

    ctx.arc(...p.arr, size, 0, Math.PI * 2);

    ctx.stroke();

}

function drawLines() {

   drawLine(line1);

   drawLine(line2);

   markPoint(line1.l1);

   markPoint(line2.l1);

   drawLine(path, "#0B0", 1);

   markPoint(path.l1, 2, "#0B0", 2);

}

function drawResult(pointAt, lineAt) {

   ctx.clearRect(0,0,W,H);

   drawLines();

   markPoint(lineAt.l1, 2, "red", 1.5);

   markPoint(lineAt.l2, 2, "red", 1.5);

   markPoint(pointAt, 2, "blue", 3);

   drawLine(lineAt, "#BA0", 2);

}

div {position: absolute; top: 10px; left: 12px}

canvas {border: 2px solid black}

<canvas id="canvas" width="1024" height="1024"></canvas>

    <div><span id="info">Click to start</span></div>

Answer 2

解决方案有两部分我不明白：

• 解决 b^2 - (a^2 + c^2) = 0而不是sqrt(b^2)-(sqrt(a^2)+sqrt(b^2)) = 0

• 返回的时间戳被限制在范围内[0,1]

也许我遗漏了一些明显的东西，但无论如何，我设计了一个解决这些问题的解决方案：

• 求解所有二次项，而不仅仅是一个

• 返回的时间戳没有限制

• sqrt(b^2)-(sqrt(a^2)+sqrt(b^2)) = 0解决了，而不是 b^2 - (a^2 + c^2) = 0

随意推荐可以优化的方法：

# pnt, crt_1, and crt_2 are points, each with x,y and dx,dy attributes

# returns a list of timestamps for which pnt is on the segment

# whose endpoints are crt_1 and crt_2

def colinear_points_collision(pnt, crt_1, crt_2):

    a, b, c, d = pnt.x, pnt.y, pnt.dx, pnt.dy

    e, f, g, h = crt_1.x, crt_1.y, crt_1.dx, crt_1.dy

    i, j, k, l = crt_2.x, crt_2.y, crt_2.dx, crt_2.dy

    m = a - e

    n = c - g

    o = b - f

    p = d - h

    q = a - i

    r = c - k

    s = b - j

    u = d - l

    v = e - i

    w = g - k

    x = f - j

    y = h - l

    # Left-hand expansion

    r1 = n * n + p * p

    r2 = 2 * o * p + 2 * m * n

    r3 = m * m + o * o

    r4 = r * r + u * u

    r5 = 2 * q * r + 2 * s * u

    r6 = q * q + s * s

    coef_a = 4 * r1 * r4  # t^4 coefficient

    coef_b = 4 * (r1 * r5 + r2 * r4)  # t^3 coefficient

    coef_c = 4 * (r1 * r6 + r2 * r5 + r3 * r4)  # t^2 coefficient

    coef_d = 4 * (r2 * r6 + r3 * r5)  # t coefficient

    coef_e = 4 * r3 * r6  # constant

    # Right-hand expansion

    q1 = (w * w + y * y - n * n - p * p - r * r - u * u)

    q2 = 2 * (v * w + x * y - m * n - o * p - q * r - s * u)

    q3 = v * v + x * x - m * m - o * o - q * q - s * s

    coef1 = q1 * q1  # t^4 coefficient

    coef2 = 2 * q1 * q2  # t^3 coefficient

    coef3 = 2 * q1 * q3 + q2 * q2  # t^2 coefficient

    coef4 = 2 * q2 * q3  # t coefficient

    coef5 = q3 * q3  # constant

    # Moves all the coefficients onto one side of the equation to get

    # at^4 + bt^3 + ct^2 + dt + e

    # solve for possible values of t

    p = np.array([coef1 - coef_a, coef2 - coef_b, coef3 - coef_c, coef4 - coef_d, coef5 - coef_e])

    def fun(x):

        return p[0] * x**4 + p[1] * x**3 + p[2] * x**2 + p[3] * x + p[4]

    # could use np.root, but I found this to be more numerically stable

    sol = optimize.root(fun, [0, 0], tol=0.002)

    r = sol.x

    uniques = np.unique(np.round(np.real(r[np.isreal(r)]), 4))

    final = []

    for r in uniques[uniques > 0]:

        if point_between(e + g * r, f + h * r, i + k * r, j + l * r, a + c * r, b + d * r):

            final.append(r)

    return np.array(final)

# Returns true if the point (px,py) is between the endpoints

# of the line segment whose endpoints lay at (ax,ay) and (bx,by)

def point_between(ax, ay, bx, by, px, py):

    # colinear already checked above, this checks between the other two.

    return (min(ax, bx) <= px <= max(ax, bx) or abs(ax - bx) < 0.001) and (min(ay, by) <= py <= max(ay, by) or abs(ay - by) < 0.001)

一个例子（L1 和 L2 是直线的端点）：

P = (0,0) with velocity (0, +1)

L1 = (-1,2) with velocity (0, -1)

L2 = (1,2) with velocity (0, -1)

返回的结果是t=1，因为在 1 个时间步后，P 将高出一个单位，而直线的两个端点将分别降低一个单位，因此，该点与线段相交于t=1。