SymPy solve(): UnboundLocalError: 局部变量

Question

我正在使用 SymPy 来求解方程，代码如下。我做了一个更简单的例子，但这个问题可能与原始方程有关，所以我会选择在这里发布原始代码而不是简化的代码。from sympy import *dP, rho, nu, D, miu, L, Q, Re, eps, f = symbols('dP, rho, nu, D, miu, L, Q, Re, eps, f')solve([Eq(Re, rho * nu * D / mu),       Eq(L / D, 0.05 * Re),       Eq(L / D, 1.359 * Re ** (1/4)),       Eq(dP, 32 * miu * L * nu / D ** 2),       Eq(dP, 128 * miu * L * Q / pi / D ** 2),       Eq(dP, f * (L/D) * (rho * nu ** 2 / 2)),       Eq(f, 64 / Re),       Eq(1 / sqrt(f), -1.8 * log ((eps / D / 3.7) ** 1.11 + 6.9 / Re))],      [Re, D, f])带有错误消息：UnboundLocalError                         Traceback (most recent call last)<ipython-input-13-884b0835e135> in <module>      7        Eq(f, 64 / Re),      8        Eq(1 / sqrt(f), -1.8 * log ((eps / D / 3.7) ** 1.11 + 6.9 / Re))],----> 9       [Re, D, f])G:\Program-Files\anaconda3\lib\site-packages\sympy\solvers\solvers.py in solve(f, *symbols, **flags)   1094         solution = _solve(f[0], *symbols, **flags)   1095     else:-> 1096         solution = _solve_system(f, symbols, **flags)   1097    1098     #G:\Program-Files\anaconda3\lib\site-packages\sympy\solvers\solvers.py in _solve_system(exprs, symbols, **flags)   1834             return rv   1835 -> 1836         solved_syms = set(solved_syms)  # set of symbols we have solved for   1837         legal = set(symbols)  # what we are interested in   1838         # sort so equation with the fewest potential symbols is firstUnboundLocalError: local variable 'solved_syms' referenced before assignment

Answer 1

那是因为你输入了错误的方程式。尝试：

solve([Eq(Re, rho * nu * D / mu),
       Eq(dP, f * (L/D) * (rho * nu ** 2 / 2)),
       Eq(1 / sqrt(f), -1.8 * log ((eps / D / 3.7) ** 1.11 + 6.9 / Re))],
      [Re, D, f])

并且错误将消失。您输入正确的方程式。

但是你会发现 SymPy 似乎无法解决这个问题。

NotImplementedError: could not solve 9*sqrt(f)*log(58510807926309*2**(11/100)*(dP*eps/(L*f*nu**2*rho))**(111/100)/125000000000000 + 69*dP*mu/(5*L*f*nu**3*rho**2)) + 5

即使经过适当的转换，我们也可以看到Re和f与 常量相关D，然而，D满足：

solve(Eq(e**(1 / (u * D ** x)), d/(D**y) + u/D),
      D)

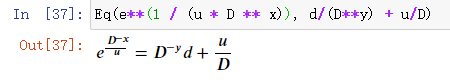
除此以外的一切D都是不变的。

它也无法通过 SymPy 解决：

NotImplementedError: multiple generators [D, D**y, e**(D**(-x)/u)]

No algorithms are implemented to solve equation e**(D**(-x)/u) - D**(-y)*d - u/D

封闭形式的解决方案可能不存在。这个方程需要用数值求解。请参阅：https://math.stackexchange.com/questions/3774718/how-to-solve-this-ln-fracax-fracbxc-frac1u-xv-where ?noredirect=1#comment7769877_3774718

所以你可以使用nsolve的sympy，意思是numerical solver。或者fsolve的scipy也可以。

from sympy import *

L = 4.11 * 10 ** 5

nu = 1

rho = 0.8175

mu = 2.88 * 10 ** -6

dP = 20000

eps = 4.6 * 10 ** -5

Re, D, f = symbols('Re, D, f')

nsolve((Eq(Re, rho * nu * D / mu),

       Eq(dP, f * L / D * rho * nu ** 2 / 2),

       Eq(1 / sqrt(f), -1.8 * log ( (eps / D / 3.) ** 1.11 + 6.9 / Re))),

      (Re, D, f), (1123, -1231, -1000))

哪里(1123, -1231, -1000)是寻找根的初始向量。它给出了：

虚部很小，都是10^(-20)，所以我们可以认为它们为零，这意味着根都是实数。Re ~ 13602.938，D ~ 0.047922 和 f~0.0057。