仅使用数学库更快地查找 n 的因数

Question

在将其标记为重复之前...我需要找到 n 的所有因数（有很多解决方案）。我能够实现的最快的一个是循环遍历 2 到 sqrt of 的范围n。这是我到目前为止...def get_factors(n):    factors = set()    for i in range(2, int(math.sqrt(n) + 1)):        if n % i == 0:            factors.update([i, n // i])    return factors这是找到 的因数的一种非常快速的方法n，但我想知道是否有更快的方法来找到 的因数n。唯一的限制是我只能在 Python 3.7 中使用数学库。关于如何更快地完成此操作的任何想法？我找不到只使用数学库的答案。我可以做些什么来提高我当前算法的效率吗？

Answer 1

最好在计算素数时获取因数，这样您就可以避免额外的工作，以防万一您在筛子完成之前完成因数分解。更新后的代码将是：

def factors(number):

    n=int(number**.5)+1

    x=number

    divisors=[]

    era =[1] * n

    primes=[]

    for p in range(2, n):

        if era[p]:

            primes.append(p)

            while x%p==0:

                x//=p

                divisors.append(p)

            for i in range(p*p, n, p):

                era[i] = False

    if x!=1:

        divisors.append(x)    

    return divisors

解决方案：

使用Erathostenes Sieve得到 2 和 sqrt(n) 之间的质因数，然后检查哪些是 n 的约数。这将大大减少代码的运行时间。

Erathostenes 筛法只使用列表、操作%,>=,<=和布尔值。

这是一个比我分享给您的链接中的实现更短的实现：

def factors(number):

    n=int(number**.5)+1

    era =[1] * n

    primes=[]

    for p in range(2, n):

        if era[p]:

            primes.append(p)

            for i in range(p*p, n, p):

                era[i] = False

    divisors=[]

    x=number

    for i in primes:

        while x%i==0:

            x//=i

            divisors.append(i)

    if x!=1:

        divisors.append(x)    

    return divisors

Answer 2

找到数字所有因素的最快方法

约束——不要使用除数学之外的任何外部库

测试了4种方法

1. 审判部门（提问者@HasnainAli 发布的代码）又名审判

2. Eratosthenes Sieve（来自@MonsieurGalois 帖子）又名 Sieve

3. 素因数分解的灵感来自aka Factorize

4. Primes based on Wheel Factorization 灵感来自Wheel Factorization aka Wheel

结果

结果是相对于试分的，即（试分时间）÷（其他方法时间）

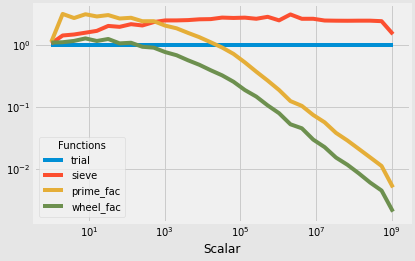
使用 timeit 的 @Davakar使用Benchit 的基准测试

N            trial  sieve     prime_fac  wheel_fac                                           

1             1.0  1.070048   1.129752   1.104619

2             1.0  1.438679   3.201589   1.119284

4             1.0  1.492564   2.749838   1.176149

8             1.0  1.595604   3.164555   1.290554

16            1.0  1.707575   2.917286   1.172851

32            1.0  2.051244   3.070331   1.262998

64            1.0  1.982820   2.701439   1.073524

128           1.0  2.188541   2.776955   1.098292

256           1.0  2.086762   2.442863   0.945812

512           1.0  2.365761   2.446502   0.914936

1024          1.0  2.516539   2.076006   0.777048

2048          1.0  2.518634   1.878156   0.690900

4096          1.0  2.546800   1.585665   0.573352

8192          1.0  2.623528   1.351017   0.484521

16384         1.0  2.642640   1.117743   0.395437

32768         1.0  2.796339   0.920231   0.327264

65536         1.0  2.757787   0.725866   0.258145

131072        1.0  2.790135   0.529174   0.189576

262144        1.0  2.676348   0.374986   0.148726

524288        1.0  2.877928   0.269510   0.107237

1048576       1.0  2.522501   0.189929   0.080233

2097152       1.0  3.142147   0.125797   0.053157

4194304       1.0  2.673095   0.105293   0.045798

8388608       1.0  2.675686   0.075033   0.030105

16777216      1.0  2.508037   0.057209   0.022760

33554432      1.0  2.491193   0.038634   0.015440

67108864      1.0  2.485025   0.029142   0.011826

134217728     1.0  2.493403   0.021297   0.008597

268435456     1.0  2.492891   0.015538   0.006098

536870912     1.0  2.448088   0.011308   0.004539

1073741824    1.0  1.512157   0.005103   0.002075

结论：

• 筛分法总是比试分法慢（即比率列> 1）

• 试用师最快达到 n ~256

• 轮分解法整体最快（即481X试分法为n = 2**30即1/0.002075~481）

代码

方式一：原帖

import math

def trial(n):

  " Factors by trial division "

  factors = set()

  for i in range(2, int(math.sqrt(n) + 1)):

      if n % i == 0:

          factors.update([i, n // i])

  return factors

方法二——筛法（@MonsieurGalois post）

def factors_sieve(number):

  " Using primes in trial division "

  # Find primes up to sqrt(n)

  n=int(number**.5)+1

  era =[1] * n

  primes=[]

  for p in range(2, n):

      if era[p]:

          primes.append(p)

          for i in range(p*p, n, p):

              era[i] = False

  # Trial division using primes

  divisors=[]

  x=number

  for i in primes:

      while x%i==0:

          x//=i

          divisors.append(i)

  if x!=1:

      divisors.append(x)    

  return divisors

方法三——基于质因数分解求除数

灵感来自

def generateDivisors(curIndex, curDivisor, arr): 

  " Yields the next factor based upon prime exponent " 

  if (curIndex == len(arr)): 

    yield curDivisor

    return

  for i in range(arr[curIndex][0] + 1): 

    yield from generateDivisors(curIndex + 1, curDivisor, arr) 

    curDivisor *= arr[curIndex][1]

def prime_factorization(n):

    " Generator for factors of n "

    # To store the prime factors along 

    # with their highest power 

    arr = [] 

    # Finding prime factorization of n 

    i = 2

    while(i * i <= n): 

      if (n % i == 0): 

        count = 0

        while (n % i == 0): 

          n //= i 

          count += 1

        

        # For every prime factor we are storing 

        # count of it's occurenceand itself. 

        arr.append([count, i])

      i += 2 if i % 2 else 1

    

    # If n is prime 

    if (n > 1): 

      arr.append([1, n]) 

    

    curIndex = 0

    curDivisor = 1

    

    # Generate all the divisors 

    yield from generateDivisors(curIndex, curDivisor, arr) 

方法四——轮式分解

def wheel_factorization(n): 

    " Factors of n based upon getting primes for trial division based upon wheel factorization "

    # Init to 1 and number

    result = {1, n}

    # set up prime generator

    primes = prime_generator()   

    # Get next prime

    i = next(primes)

    while(i * i <= n): 

      if (n % i == 0):

        result.add(i)

        

        while (n % i == 0): 

          n //= i 

          result.add(n)

      i = next(primes)  # use next prime

    return result

def prime_generator():

  " Generator for primes using trial division and wheel method "

  yield 2; yield 3; yield 5; yield 7;

  def next_seq(r):

    " next in the equence of primes "

    f = next(r)

    yield f

    r = (n for n in r if n % f)  # Trial division

    yield from next_seq(r)

  def wheel():

    " cycles through numbers in wheel whl "

    whl = [2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2,

          6, 4, 6, 8, 4, 2, 4, 2, 4, 8, 6, 4, 6, 2, 4, 6,

          2, 6, 6, 4, 2, 4, 6, 2, 6, 4, 2, 4, 2, 10, 2, 10]

    

    while whl:

      for element in whl:

        yield element

  def wheel_accumulate(n, gen):

    " accumulate wheel numbers "

    yield n

    total = n

    for element in gen:

      total += element

      yield total

  for p in next_seq(wheel_accumulate(11, wheel())):

    yield p

测试代码

from timeit import timeit

cnt = 100000  # base number of repeats for timeit

print('{0: >12} {1: >9} {2: >9} {3: >9} {4: >9}'.format('N', 'Trial', 'Primes', 'Division', 'Wheel'))

for k in range(1, 31):

  N = 2**k

  count = cnt // k   # adjust repeats based upon size of k

  x = timeit(lambda:trial(N), number=count)

  y = timeit(lambda:sieve(N), number=count)

  z = timeit(lambda:list(prime_factorization(N)), number=count)

  k = timeit(lambda:list(wheel_factorization(N)), number=count)

  print(f"{N:12d} {1:9d} {x/y:9.5f} {x/z:9.5f} {x/k:9.5f}")