是否有等效于 numpy.linalg.pinv 的 JavaScript？

Question

我正在尝试解决一个线性方程组，该方程组是超定的 (Ax = B)，给定一个矩阵 A，该矩阵 A 由用户在网站上使用 Javascript 输入生成。在 python 中，我可以使用 numpy.linalg.pinv(A) 来找到 A 的伪逆并将该伪逆乘以 B 来求解系统——是否有一个 JavaScript 等效的（库和/或一段代码）可以做这个？我尝试使用 math.js；虽然它似乎没有伪逆函数，但它有其他矩阵运算。我尝试使用math.multiply(math.inv(math.multiply(math.transpose(A), A)), math.transpose(A))找到伪逆，但我从 A 的转置乘以 A 得到的矩阵不可逆，因为 A 的列显然是线性相关的（我对线性代数不是很熟悉，但这是我从一些研究中收集到的在线）。然而，即使矩阵 A 具有线性相关列（我用 numpy 测试了系统），numpy 仍然可以找到伪逆函数，这让我回到了是否有办法复制 numpy 的伪逆函数的问题。如果没有，是否有其他解决方案可以解决此问题？

Answer 1

问： 如果没有，是否有其他解决方案可以解决此问题？

是的，有办法。

实施分布式处理工作流。让 JavaScript 发挥它的作用，让numpySide 完成它非常擅长的工作。类似的概念在许多用例中很常见，其中专用工具解决部分问题，一些工作流集成中介将分布式部分“粘合”在一起。

因此，让 JavaScript 部分配备 ZeroMQ/zmq或nanomsg，A, B通过互连与 python 端通信，那里 numpy 将尽其所能进行智能、矢量化的数字处理，并让接收到的结果传回下一个阶段处理工作流。

ZeroMQ 多年来拥有用于非常快速和高效的无协议{ ipc:// | vmci:// }本地主机互连的智能工具，此外还有用于{ tcp:// | udp:// | ... }数据中心互连的类似智能但非本地的协议，如果你的本地主机资源对于更大的矩阵大小会变得非常小。

有类似的工具准备就绪nanomsg，但您必须检查 JavaScript 端可用端口/包装器的可用性。

剩下的就是为任何给定的数据量和前端/后端事务运行的请求节奏挤出最大性能。

在~ 80 [ms]您的想象力下使用此架构进行周转时间是您的极限。也尽可能快地完成了一些多TB线性代数处理，在那里需要更加小心，但性能驱动的原则是相同的。

Answer 2

我知道自从提出这个问题已经有一段时间了，但是现在（2021 年）有一些用于在 JS 中进行线性代数的库，我将其留在这里以供参考：

• 矩阵

• 本征

• 线性代数js

• 埃姆拉帕克

• linalg.js

仅举几例。从您的问题来看，您似乎正在尝试解决最小二乘估计量：

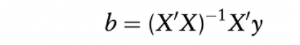
如果是这种情况，与计算伪逆（即使用 LU/QR/SVD 分解）相比，上述库中的大多数（全部？）提供了更稳健/高性能的解决方案：

// Using ml-matrix

const { Matrix, solve } = require('ml-matrix');

var X = new Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]);

var y = Matrix.columnVector([8, 20, 32]);

var b = solve(X, y, (useSVD = true));

// Using linear algebra js

const { SparseMatrix, DenseMatrix } = require('linear-algebra');

// solve the linear system Ax = b, where A is a square sparse matrix

var X = SparseMatrix.identity(5, 5);

var y = DenseMatrix.ones(5, 1);

var lu = X.lu();

var b = lu.solveSquare(y);

但是，如果你真的需要计算伪逆，ml-matrix 是唯一支持这个的库（据我所知）。原则上，Eigen 也支持此功能，但我还没有看到任何 JS 端口实际公开此功能。