解释如何在循环链表中查找循环起始节点？

Question

我知道Tortoise和Hare的会议总结了循环的存在，但是如何将乌龟移动到链接列表的开头，同时又将野兔保留在聚会地点，然后一次移动两个步骤，使它们在循环的起点相遇呢？

Answer 1

这是用于循环检测的弗洛伊德算法。您正在询问算法的第二阶段-找到一个节点是周期的一部分后，如何找到周期的起点？

在弗洛伊德算法的第一部分中，野兔为乌龟的每一步移动了两步。如果乌龟和野兔相遇过，就会有一个循环，并且集合点是循环的一部分，但不一定是循环中的第一个节点。

当乌龟和野兔相遇时，我们找到了最小的i（乌龟采取的步数），使得X _i = X _2i。令mu代表从X ₀到循环开始的步数，令lambda代表循环的长度。然后，i = mu + a lambda，而2i = mu + b lambda，其中a和b是整数，表示乌龟和野兔在循环中跑了多少次。从第二个方程中减去第一个方程可得出i =（ba）* lambda，因此i是lambda的整数倍。 因此，X _{i + mu} = X _mu。X _i代表乌龟和野兔的交汇点。如果您将乌龟移回起始节点X₀，然后让乌龟和野兔以相同的速度继续前进，经过多步，乌龟将达到X _mu，野兔将达到X _{i + mu} = X _mu，因此第二个相遇点表示乌龟的开始周期。

Answer 2

参考此图片：

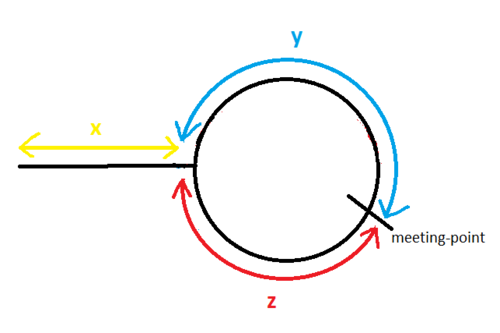
慢速指针在会议之前经过的距离 = x + y

在会议之前fastPointer行驶的距离 =（x + y + z）+ y = x + 2y + z

由于fastPointer行驶过程中双 slowPointer的速度，时间是恒定的，当到达会合点两种。

因此，通过使用简单的速度，时间和距离关系2（x + y）= x + 2y + z => x + 2y + z = 2x + 2y => x = z

因此，通过将slowPointer移动到链接列表的开头，并使slowPointer和fastPointer一次移动一个节点，它们的覆盖距离相同。

它们将到达循环列表中循环开始的位置。