圆-矩形碰撞检测(相交)

Question

圆-矩形碰撞检测(相交)如何判断二维欧几里德空间中的圆与矩形是否相交？(即经典的二维几何)

Answer 1

当圆与矩形相交时，只有两种情况：

• 要么圆心位于矩形内，要么
• 矩形的一个边在圆中有一个点。

请注意，这并不要求矩形是轴平行的。

(一种观察方法是：如果圆中没有一个点(如果所有的边都“在”圆之外)，那么圆仍然可以与多边形相交的唯一方法是它完全位于多边形内。)

有了这个洞察力，下面这样的东西就能工作了，在那里圆圈有中心。P半径R，而矩形具有顶点。A, B, C, D按照这个顺序(不完整的代码)：

def intersect(Circle(P, R), Rectangle(A, B, C, D)):
    S = Circle(P, R)
    return (pointInRectangle(P, Rectangle(A, B, C, D)) or
            intersectCircle(S, (A, B)) or
            intersectCircle(S, (B, C)) or
            intersectCircle(S, (C, D)) or
            intersectCircle(S, (D, A)))

如果您正在编写任何几何学，您可能已经在您的库中具有上述功能。否则，pointInRectangle()可以通过多种方式实现；多边形点方法可以工作，但对于矩形，只需检查此方法是否有效：

0 ≤ AP·AB ≤ AB·AB and 0 ≤ AP·AD ≤ AD·AD

和intersectCircle()也很容易实现：一种方法是检查垂直于P到行足够近，并且在端点之间，否则检查终结点。

最酷的是同IDEA不仅适用于矩形，而且适用于圆与任意一个圆的交点。简单多边形-甚至不一定是凸的！

Answer 2

我会这样做：

bool intersects(CircleType circle, RectType rect)
{
    circleDistance.x = abs(circle.x - rect.x);
    circleDistance.y = abs(circle.y - rect.y);

    if (circleDistance.x > (rect.width/2 + circle.r)) { return false; }
    if (circleDistance.y > (rect.height/2 + circle.r)) { return false; }

    if (circleDistance.x <= (rect.width/2)) { return true; } 
    if (circleDistance.y <= (rect.height/2)) { return true; }

    cornerDistance_sq = (circleDistance.x - rect.width/2)^2 +
                         (circleDistance.y - rect.height/2)^2;

    return (cornerDistance_sq <= (circle.r^2));
}

下面是它的工作原理：

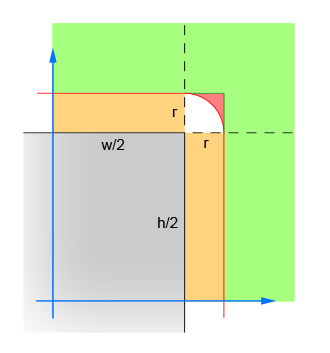
1. 第一对直线计算圆心和矩形中心之间x和y差值的绝对值。这会将四个象限折叠成一个，这样计算就不必再做四次了。这张图显示了圆心现在必须放置的区域。注意，只显示了一个象限。矩形是灰色区域，红色边框勾勒出与矩形边缘正好有一个半径的临界区域。圆的中心必须在这个红色的边界内，才能发生交点。

2. 第二对线消除了简单的情况，即圆离矩形足够远(在任一方向)，不可能相交。这与图像中的绿色区域相对应。

3. 第三对线处理简单的情况，即圆足够接近矩形(在任一方向)，以保证一个交点。这对应于图像中的橙色和灰色部分。注意，这个步骤必须在步骤2之后完成，这样逻辑才有意义。

4. 其余的线计算出圆圈可能与矩形角相交的困难情况。若要求解，请计算从圆心到拐角的距离，然后验证距离不大于圆的半径。此计算对中心位于红色阴影区域内的所有圆返回false，对于中心位于白阴影区域内的所有圆返回true。