从n返回k个元素的所有组合的算法我想写一个函数，它将一个字母数组作为参数，并选择一些字母。假设您提供了8个字母的数组，并希望从中选择3个字母。然后你应该得到：8! / ((8 - 3)! * 3!) = 56数组（或单词）返回，每个包含3个字母。
4 回答
慕后森
TA贡献1802条经验 获得超5个赞
计算机编程艺术第4卷：分册3有很多这些可能比我描述的更适合你的特殊情况。
格雷码
你会遇到的一个问题当然是记忆而且非常快，你的组中有20个元素会出现问题 - 20 C 3 = 1140.如果你想迭代这个集合，最好使用修改后的灰色代码算法，所以你没有把所有这些都保存在内存中。这些产生了前一个的下一个组合，避免重复。其中有许多用于不同的用途。我们是否希望最大化连续组合之间的差异？最小化？等等。
一些描述格雷码的原始论文：
以下是一些涉及该主题的其他文章：
Eades，Hickey，读取相邻交换组合生成算法的有效实现（PDF，代码为Pascal）
组合灰度代码调查（PostScript）
Chase's Twiddle（算法）
Phillip J Chase，“ 算法382：N个物体中M的组合 ”（1970）
C中的算法 ...
字典顺序中的组合索引（带扣算法515）
您还可以通过其索引（按字典顺序）引用组合。根据索引意识到索引应该是从右到左的一些变化，我们可以构造一些应该恢复组合的东西。
所以，我们有一套{1,2,3,4,5,6} ......我们需要三个元素。让我们说{1,2,3}我们可以说元素之间的差异是一个，有序和最小。{1,2,4}有一个变化，按字典顺序排列第2位。因此，最后一个地方的“变化”数量占字典顺序的一个变化。第二个位置，只有一个变化{1,3,4}有一个变化，但由于它位于第二位（与原始集合中的元素数量成比例），因此会有更多变化。
我所描述的方法是解构，似乎从设置到索引，我们需要反向 - 这更加棘手。这就是Buckles如何解决这个问题。我写了一些C来计算它们，只需稍作修改 - 我使用集合的索引而不是数字范围来表示集合，所以我们总是从0 ... n开始工作。注意：
由于组合是无序的，{1,3,2} = {1,2,3} - 我们将它们命名为词典。
此方法具有隐式0以启动第一个差异的集合。
字典顺序中的组合索引（McCaffrey）
还有另外一种方法：它的概念更易于掌握和编程，但它没有Buckles的优化。幸运的是，它也不会产生重复的组合：
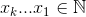
最大化的集合
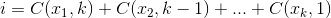
在哪里
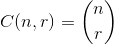
举个例子：27 = C(6,4) + C(5,3) + C(2,2) + C(1,1)。因此，第四十七个词典组合的四个事物是：{1,2,5,6}，这些是你想要看的任何集合的索引。下面的示例（OCaml）需要choose功能，留给读者：
(* this will find the [x] combination of a [set] list when taking [k] elements *)let combination_maccaffery set k x = (* maximize function -- maximize a that is aCb *) (* return largest c where c < i and choose(c,i) <= z *) let rec maximize a b x = if (choose a b ) <= x then a else maximize (a-1) b x in let rec iterate n x i = match i with | 0 -> [] | i -> let max = maximize n i x in max :: iterate n (x - (choose max i)) (i-1) in if x < 0 then failwith "errors" else let idxs = iterate (List.length set) x k in List.map (List.nth set) (List.sort (-) idxs)
一个小而简单的组合迭代器
提供以下两种算法用于教学目的。它们实现了迭代器和（更一般的）文件夹整体组合。它们尽可能快，具有复杂度O（n C k）。内存消耗受到约束k。
我们将从迭代器开始，它将为每个组合调用用户提供的函数
let iter_combs n k f = let rec iter v s j = if j = k then f v else for i = s to n - 1 do iter (i::v) (i+1) (j+1) done in iter [] 0 0
更通用的版本将从初始状态开始调用用户提供的函数以及状态变量。因为我们需要在不同状态之间传递状态，所以我们不会使用for循环，而是使用递归，
let fold_combs n k f x = let rec loop i s c x = if i < n then loop (i+1) s c @@ let c = i::c and s = s + 1 and i = i + 1 in if s < k then loop i s c x else f c x else x in loop 0 0 [] x
开满天机
TA贡献1786条经验 获得超12个赞
在C＃中：
public static IEnumerable<IEnumerable<T>> Combinations<T>(this IEnumerable<T> elements, int k)
{
return k == 0 ? new[] { new T[0] } :
elements.SelectMany((e, i) =>
elements.Skip(i + 1).Combinations(k - 1).Select(c => (new[] {e}).Concat(c)));
}
用法：
var result = Combinations(new[] { 1, 2, 3, 4, 5 }, 3);
结果：
123
124
125
134
135
145
234
235
245
345
陪伴而非守候
TA贡献1757条经验 获得超8个赞
短java解决方案：
import java.util.Arrays;
public class Combination {
public static void main(String[] args){
String[] arr = {"A","B","C","D","E","F"};
combinations2(arr, 3, 0, new String[3]);
}
static void combinations2(String[] arr, int len, int startPosition, String[] result){
if (len == 0){
System.out.println(Arrays.toString(result));
return;
}
for (int i = startPosition; i <= arr.length-len; i++){
result[result.length - len] = arr[i];
combinations2(arr, len-1, i+1, result);
}
}
}
结果将是
[A, B, C]
[A, B, D]
[A, B, E]
[A, B, F]
[A, C, D]
[A, C, E]
[A, C, F]
[A, D, E]
[A, D, F]
[A, E, F]
[B, C, D]
[B, C, E]
[B, C, F]
[B, D, E]
[B, D, F]
[B, E, F]
[C, D, E]
[C, D, F]
[C, E, F]
[D, E, F]
芜湖不芜
TA贡献1796条经验 获得超7个赞
我可以提出我的递归Python解决方案来解决这个问题吗？
def choose_iter(elements, length):
for i in xrange(len(elements)):
if length == 1:
yield (elements[i],)
else:
for next in choose_iter(elements[i+1:len(elements)], length-1):
yield (elements[i],) + next
def choose(l, k):
return list(choose_iter(l, k))
用法示例：
>>> len(list(choose_iter("abcdefgh",3)))
56
我喜欢它的简单性。
添加回答
举报
0/150
提交
取消