顶点：  

顶点索引               出弧链表头指针                         顶点数据

    |                                  |                                           |

顶点索引      第一个出弧的指针(可以是NULL)         顶点数据

弧的表示方法：

弧头顶点索引                下一条弧指针                  弧数据

         |                                    |                                |

弧头顶点(指向的点)        一个点有多个弧              弧数据

                               每个弧保存下一条弧的指针

邻接表表达图：

顶点和图：

顶点保存点的索引和数据

图保存顶点数组和邻接矩阵

邻接矩阵方法：

图->数据

图的存储结构：

    邻接矩阵(数组)

    邻接表(链表)-->存储有向图

    十字链表(链表)-->存储有向图

    邻接多重表(链表) -->无向图

【图的遍历】深度优先搜索（前序遍历）、广度优先搜索（一层一层搜索）

【最小生成树】普里姆Prim算法、克鲁斯卡尔Kruskal算法

1、Prim算法

• 点集合

• 边集合

• 待选边集合

2、Kruskal算法

• 待选边集合

• 已选边集合

• 已涉及点集合
  

1、十字链表-链式存储

• 顶点的表示：顶点索引+顶点数据+以该顶点为弧尾的弧节点指针+以该节点为弧头的弧节点指针

• 弧：弧尾顶点索引+弧头顶点索引+弧尾相同的下一条弧的指针+弧头相同的下一条弧的指针+弧的数据

• struct Arc{弧尾顶点索引；弧头顶点索引；指向下一条弧头相同的弧的指针；指向下一条弧尾相同的弧的指针；弧的数据；}

• struct Node{顶点索引；顶点数据；第一条入弧节点指针；第一条出弧节点指针；}

• struct Map{顶点数组；}

2、邻接多重表-链式存储（无向图）

• 顶点：顶点索引+连接该顶点的边+顶点数据

• 边：A顶点索引+B顶点索引+与A顶点相连接的下一条边的指针+与B顶点相连接的下一条边的指针+边的数据

• struct Edge{顶点A索引；顶点B索引；连接A的下一条边的指针；连接B的下一条边的指针；边信息；}

• struct Node{顶点索引；顶点数据；第一条边节点的指针；}

• struct Map{顶点数组；}
  

【图的存储结构】邻接矩阵（用数组表达）、邻接表（链表，有向图）、十字链表（链表，有向图）、邻接多重表（链表，用于表达无向图）

【权值】弧/边上的数据（比如两个城市之间的某条公路是300km）

1、邻接矩阵

• 顶点的表示：顶点索引+顶点数据

• 有弧的用1表示，没有弧的用0表示，自己和自己用0

• 

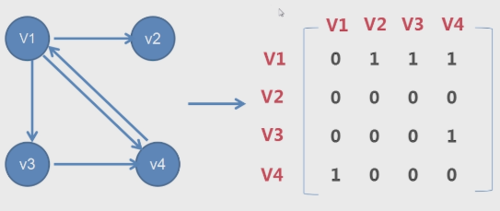
• int matrix[4][4];

• struct Node{顶点索引；顶点数据；}

• struct Map{顶点数组；邻接矩阵；}

2、邻接表-链式存储

• 顶点的表示：顶点索引+出弧链表头指针+顶点数据

• 弧：弧头顶点索引+下一条弧指针+弧数据

• 逆邻接表：记录的是 入弧链表头指针 和 弧尾顶点索引

• struct Node{顶点索引；该顶点弧链表的头结点；顶点数据；}

• struct Arc{指向的顶点索引；指向下一条弧的指针；弧信息；}

• struct Map{顶点数组；}
  

【图】无向图、有向图

【有向图】每个节点都叫做“顶点”，顶点之间的有方向的连线叫做“弧”

• 方向箭头的尾端：弧尾

• 方向箭头的头端：弧头

• 某个顶点发射出去的箭头数：出度（数）

• 某个顶点接受到的箭头数：入度（数）

【无向图】节点为“顶点”；节点间的连线是无方向的（即可以看做双向的），叫做“边”；由边连接的两个顶点为邻接点

• 连通图：每个顶点都有通往其他顶点的连线（直接/间接）

• 完全图：任意顶点都与其他顶点有直接的连线，边数=n(n-1)/2

• 生成树：最少数量的边连接每一个顶点，边数=n-1

邻接表与逆邻接表:

顶点：顶点索引，出弧链表头指针，顶点数据；

弧：弧头顶点索引，吓一跳弧指针，弧数据

顶点结构体：包括顶点索引和顶点数据;

图的结构体：包括顶点数组和邻接矩阵

顶点结构体：包括顶点索引和顶点数据就行 图的结构体：包括顶点数组（记录顶点）和邻接矩阵（记录边，并且顶点和边的关系）就行 邻接表与逆邻接表：相对于弧的出入顶点说的，如果存储的是弧出顶点的就是邻接表，如果存储的是弧进顶点就是逆邻接表

不用看第二遍

/**	
* 广度优先遍历	(java实现)
*/	
public void breadthFirstTraverse(int nodeIndex) {	
	System.out.print(NodeArray[nodeIndex].date+"  ");	
	NodeArray[nodeIndex].isVistited = true;		
	Vector<Integer> v1 = new Vector<Integer>();		
	v1.add(nodeIndex);		
	breadthFirst(v1);	
}		
public void breadthFirst(Vector<Integer> v1) {	
	int[] value = new int[1];		
	Vector<Integer> v2 = new Vector<Integer>();		
	for(int j = 0; j < (int)v1.size() ; j++) {			
	    for(int i = 0; i < Capacity ; i++) {				
	        getValueFromMatrix(v1.get(j), i, value);
	        if(value[0] != 0) {
	    	    if(NodeArray[i].isVistited) {
	    	        continue;
	    	    }else {
	    	        System.out.print(NodeArray[i].date+"  ");
	    	        NodeArray[i].isVistited = true;
	    	        v2.add(i);
	    	    }
	        }
	    }
     }
     if(v2.size() == 0) {
         return;
     }else {
         breadthFirst(v2);
     }
}