动态规划——矩阵连乘（算法设计课题）

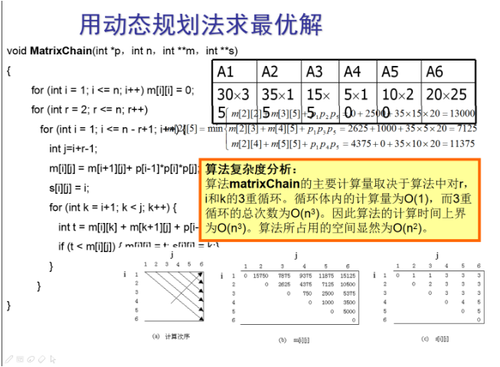
问题描述：给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。例如：A1={30x35} ; A2={35x15} ;A3={15x5} ;A4={5x10} ;A5={10x20} ;A6={20x25} 最后的结果为：((A1(A2A3))((A4A5)A6))  最小的乘次为15125。

解题思路：能用动态规划的一个性质就是最优子结构性质，也就是说计算A[i:j]的最优次序所包含的计算矩阵子琏A[i:k]和A[k+1:j]的次序也是最优的。动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算（即先从最小的开始计算）。在计算过程中，保存已解决的子问题答案。每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量的重复计算，最终得到多项式时间的算法。我们可以根据下面这个公式来计算结果。其中p[i-1]表示的是第i个矩阵的行数,p[k]表示i:k矩阵合起来后最后得到的列数，p[j]是k+1:j合起来后得到的列数。这个部分的计算方法其实就是计算两个矩阵相乘时总共的乘次数。

从连乘矩阵个数为2开始计算每次的最小乘次数m[i][j]: m[0][1] m[1][2] m[2][3] m[3][4] m[4][5]  //m[0][1]表示第一个矩阵与第二个矩阵的最小乘次数

然后再计算再依次计算连乘矩阵个数为3：m[0][2] m[1][3] m[2][4] m[3][5]
　　　　　　　　　   连乘矩阵个数为4：m[0][3] m[1][4] m[2][5]
　　　　　　　　　　连乘矩阵个数为5：m[0][4] m[1][5]
　　　　　　　　　　连乘矩阵个数为6：m[0][5]    //即最后我们要的结果

#include<stdio.h>int p[101],m[101][101],s[101][101];int n;void matrixChain(){for(int i=1;i<=n;i++)m[i][i]=0;for(int r=2;r<=n;r++)for(int i=1;i<=n-r+1;i++){int j = r+i-1;m[i][j]=m[i][i]+m[i+1][j]+p[i-1]*p[i]*p[j];s[i][j]=i;for(int k = i+1;k<j;k++){int temp=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];if(temp<m[i][j]){m[i][j]=temp;s[i][j]=k;}}}}void traceback(int i,int j){if(i==j)return ;traceback(i,s[i][j]);traceback(s[i][j]+1,j);printf("Multiply A[%d,%d]and A[%d,%d]\n",i,s[i][j],s[i][j]+1,j);}int main(){while(~scanf("%d",&n)){for(int i=0;i<=n;i++)scanf("%d",&p[i]);matrixChain();traceback(1,n);printf("%d\n",m[1][n]);}return 0;}