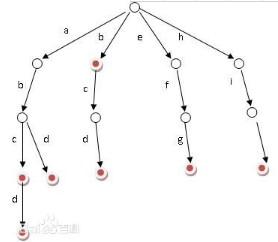
字典树:又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
它有3个基本性质:
根节点不包含字符,除根节点外每一个节点都只包含一个字符; 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串; 每个节点的所有子节点包含的字符都不相同。
搜索字典项目的方法为:
(1) 从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
(3) 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……
(5) 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
以上为百科说明。我们再通俗的解释一下,字典树其实也是一种索引、映射。唯一的优势就是,他能够很快速的指定偏移量(即将字符与偏移量达成了关系)
比如说*s-'a' 即a0,b1……,当我们找c的时候,我们可以直接寻找其数组编号为[2]的内存地址单元。而构造到达当前节点完整路径就是我们引入的单词
所以我们的定义是这样的:
#define MAX 26
typedef struct TrieNode //Trie结点声明
{
bool isStr; //标记该结点处是否构成单词
struct TrieNode *next[MAX]; //儿子分支
}Trie;
所以我们看到字典树的时间复杂度与有多少个单词没有任何关系,其时间复杂度为单词的长度,而空间复杂度是单词长度的26^长度(我们先假设是英文,英文26个字母)
我们现在知道字典树的强大之处了,那么如何运用呢?
首先看一下插入
①如果当前节点不存在(深度不够),建立节点
②如果构造当前节点的路径(就是单词)未被标记,那么标记改点为单词
是不是很简单呢?查询更简单!直接递归往下搜嘛!!
下面给出字典树代码
#include <iostream> #include<cstdlib> #define MAX 26 using namespace std;typedef struct TrieNode //Trie结点声明 { bool isStr; //标记该结点处是否构成单词 struct TrieNode *next[MAX]; //儿子分支 }Trie;void insert(Trie *root,const char *s) //将单词s插入到字典树中 {if(root==NULL||*s=='\0')return;int i;Trie *p=root;while(*s!='\0'){if(p->next[*s-'a']==NULL) //如果不存在,则建立结点 {Trie *temp=(Trie *)malloc(sizeof(Trie));for(i=0;i<MAX;i++){temp->next[i]=NULL;}temp->isStr=false;p->next[*s-'a']=temp;p=p->next[*s-'a'];}else{p=p->next[*s-'a'];}s++;}p->isStr=true; //单词结束的地方标记此处可以构成一个单词 }int search1(Trie *root,const char *s) //完全对齐{ Trie *p=root;while(p!=NULL&&*s!='\0'){p=p->next[*s-'a'];s++;}return (p!=NULL&&p->isStr==true); }int search2(Trie *root,const char *s) //头对齐{Trie *p=root;while(p!=NULL&&*s!='\0'){if(p->isStr==true){ return 1; }p=p->next[*s-'a'];s++;}return (p!=NULL&&p->isStr==true);}int search3(Trie *root,const char *s) //尾对齐 {while(*s!='\0'){ if(search1(root,s)) return 1; else s++; } return 0;}int search4(Trie *root,const char *s) //检索 {while(*s!='\0'){ if(search2(root,s)) return 1; else s++; } return 0;}void del(Trie *root) //释放整个字典树占的堆区空间 {int i;for(i=0;i<MAX;i++){if(root->next[i]!=NULL){del(root->next[i]);}}free(root);}int main(int argc, char *argv[]) {int i;int n,m; //n为建立Trie树输入的单词数,m为要查找的单词数 char s[100];Trie *root= (Trie *)malloc(sizeof(Trie));for(i=0;i<MAX;i++){root->next[i]=NULL;}root->isStr=false;scanf("%d",&n);getchar();for(i=0;i<n;i++) //先建立字典树 {scanf("%s",s);insert(root,s);}while(scanf("%d",&m)!=EOF){for(i=0;i<m;i++) //查找 {scanf("%s",s);if(search4(root,s)==1){ printf("YES\n"); }elseprintf("NO\n");}printf("\n");}del(root); //释放空间很重要 return 0;}我们看到,其头对齐(完全对齐)查询操作比较简单,显然,因为字典树是从首字母一层一层构造的,那么如果我们不是从头对齐的话,比如说检测一段文本敏感词,就只能走一套循环了。
字典树在我工作中实际遇到过,就是敏感词检索。并且是中文,所以我们只能将MAX设为256。
我以GBK编码格式存储中文,因为GBK始终占2个单元便于管理以及后续的需求变更
但是大家知道,GBK第一个汉字是负值的,所以我们需要一个处理,即:
int GetCharFromGBK(char gbk_buf){ int value=0; value=gbk_buf;return value>0?value:value+256;}提供一个测试demo的完整工程下载地址http://download.csdn.net/detail/sm9sun/9691486
含有编码转换、特殊符号处、繁体字替换等处理。
共同学习,写下你的评论
评论加载中...
作者其他优质文章