人工智障学习笔记——机器学习(8)K均值聚类

一.概念

K均值聚类(K-means)是硬聚类算法，是典型的基于原型的目标函数聚类方法的代表，它是数据点到原型的某种距离作为优化的目标函数，利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度，它是求对应某一初始聚类中心向量V最优分类，使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。

二.算法
1）从数据中随机选取K组数据作为质心centroids
2）对剩余的数据依次计算其到每个质心的距离，并把它归到最近的质心的类
3）重新计算已经得到的各个类的质心
4）迭代2～3步直至新的质心与原质心相等或小于指定阈值，算法结束

三.实现

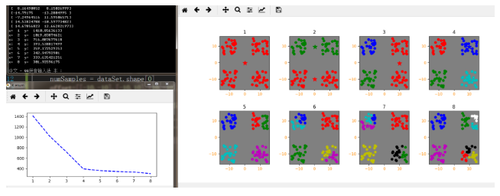
# -*- coding: utf-8 -*-  from numpy import *import timeimport matplotlib.pyplot as plt#随机200个坐标点 (-10~10)def getdataSet():dataSet=mat(zeros((100, 2)))numSamples = dataSet.shape[0]offset=[[-10,-10],[-10,10],[10,-10],[10,10]]#分类for i in range(numSamples):dataSet[i] =random.uniform(-5,5)+offset[i%4][0],random.uniform(-5,5)+offset[i%4][1]#偏移return dataSet# 欧式距离def euclDistance(vector1, vector2):	return sqrt(sum(power(vector2 - vector1, 2)))# 总误差def getcost(clusterAssment):  len = clusterAssment.shape[0]Sum = 0.0  for i in range(len):Sum = Sum + clusterAssment[i, 1]return Sum# 用随机样本初始化centroids  def initCentroids(dataSet, k):  numSamples, dim = dataSet.shapecentroids = zeros((k + 1, dim))s = set()for i in range(1, k + 1):while True:index = int(random.uniform(0, numSamples))#随机数去重if index not in s:s.add(index)break        centroids[i, :] = dataSet[index, :]return centroids# k-means主算法def kmeans(dataSet, k):numSamples = dataSet.shape[0]# 第一列存这个样本点属于哪个簇# 第二列存这个样本点和样本中心的误差clusterAssment = mat(zeros((numSamples, 2)))for i in range(numSamples):clusterAssment[i, 0] = -1clusterChanged = True# step 1: 初始化centroidscentroids = initCentroids(dataSet, k)# 如果收敛完毕，则clusterChanged为Falsewhile clusterChanged:clusterChanged = False# 对于每个样本点for i in range(numSamples):minDist = 0xfffffminIndex = 0# 对于每个样本中心# step 2: 找到最近的样本中心for j in range(1, k + 1):distance = euclDistance(centroids[j, :], dataSet[i, :])if distance < minDist:minDist = distanceminIndex = j# step 3: 更新样本点与中心点的分配关系if clusterAssment[i, 0] != minIndex:clusterChanged = TrueclusterAssment[i, :] = minIndex, minDistelse:clusterAssment[i, 1] = minDist# step 4: 更新样本中心     for j in range(1, k + 1):pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]centroids[j, :] = mean(pointsInCluster, axis=0)return centroids, clusterAssmentx=[1, 2, 3, 4, 5, 6, 7, 8]y=[0, 0, 0, 0, 0, 0, 0, 0]dataSet =getdataSet()print(dataSet)plt.figure('k-means',figsize=(12, 6))for index in range(8):k = x[index]centroids, clusterAssment = kmeans(dataSet, k)#print(clusterAssment)y[index]=getcost(clusterAssment)print("x: ",k," y: ",y[index])plt.subplot(2, 4, index+1,facecolor=(0.5,0.5,0.5))numSamples, dim = dataSet.shapemark = ['or', 'og', 'ob', 'oc', 'om', 'oy', 'ok', 'ow']for i in range(numSamples):markIndex = int(clusterAssment[i, 0])plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex-1])mark = ['*r', '*g', '*b', '*c', '*m', '*y', '*k', '*w']for i in range(1,k+1):plt.plot(centroids[i, 0], centroids[i, 1], mark[i-1], markersize = 12)plt.subplots_adjust(wspace=0.4, hspace=0.4)plt.xticks(fontsize=10, color="darkorange")plt.yticks(fontsize=10, color="darkorange")plt.title(index+1)plt.figure('K enum',figsize=(6, 3))plt.plot(x, y, "b--", linewidth=2)plt.show()

这里在getdataSet随机数据点中加入了偏移量影响，可以看出数据分布大概在四角方向，显然K=4效果应最好。

通过程序输出的不同K值误差（clusterAssment）总和也可以看出，当K>4后分类的增多确实已经不会再对误差产生太大的优化了，反而看起来乱乱的。

故合理的确定K值对于聚类效果的好坏有很大的影响。

四.K-Means ++ 算法

除了要确定K值外，Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。故而衍生了 k-means++算法。

 k-means++算法选择初始聚类中心的基本思想就是：初始的聚类中心之间的相互距离要尽可能的远。

1.从输入的数据点集合中随机选择一个点作为第一个聚类中心
2.对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
3.选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
4.重复2和3直到k个聚类中心被选出来
利用这k个初始的聚类中心来运行标准的k-means算法

从上面的算法描述上可以看到，算法的关键是第3步，如何将D(x)反映到点被选择的概率上，一种算法如下：
先从我们的数据库随机挑个随机点当“种子点”
对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。
重复2和3直到k个聚类中心被选出来
利用这k个初始的聚类中心来运行标准的k-means算法
可以看到算法的第三步选取新中心的方法，这样就能保证距离D(x)较大的点，会被选出来作为聚类中心了。

代码可以参考http://rosettacode.org/wiki/K-means%2B%2B_clustering

五.总结

 k-means算法比较简单，和之前说过的K近邻算法(KNN)http://blog.csdn.net/sm9sun/article/details/78521927有些类似，本质上都是给定一个点，然后在数据集中找邻近的点。但又有些区别：

首先KNN是分类算法，而K-means是聚类算法，KNN是监督学习，而K-means是非监督学习。也就是说，KNN拿到的数据集是已经是有分类的数据了，而K-means拿到的数据是无分类的，经过聚类后才有了类的标志。且K的定义也完全不一样，K-means的K值是需要提前指定的，通过上述代码也可以看出，K的选取至关重要。但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。且K-means应用局限性非常大，聚类的算法公式还需实际情况而变。

六.相关学习资源

http://blog.csdn.net/loadstar_kun/article/details/39450615

http://blog.csdn.net/eventqueue/article/details/73133617

http://blog.csdn.net/zouxy09/article/details/17589329