全排列及相关扩展算法（二）——求字典序下一组排列及全排列算法

1.字典序排列的定义：为了便于理解，以数字为例，对于数字1、2、3......n的排列，不同排列的先后关系是从左到右逐个比较对应的数字的先后来决定的。例如对于5个数字的排列 12354和12345，排列12345在前，排列12354在后。按照这样的规定，5个数字的所有的排列中最前面的是12345，最后面的是 54321。

2.字典序排列解决思路：参考上文中（1，2，3，4）全排列的输出截图最后输出的是（4，1，2，3），并不是我们要求的字典序排列。不难看出字典序最前面的为递增序列，最后面的位递减序列，假设我们求字典序中一组排列的下一组排列，我们即可从最后一位往前找，直到找到某一位(i)比其其后一位(i+1)小，那么说明i之前的位数皆已确定，接下来只需要找到i后面最小的且比i位数大的那一位与i交换作为第i位数（因为在此之前，i后面的位置必然是以递减的形式存在的），交换后i后面位数按递增排序，即可构造出原排列的下一组排列。

举个例子：假设求12453后一组排列

①从最后一位1遍历，3比5小，往前走

②5比4大，记录此时位置为i，故i之前的位（12）不变

③遍历i后面数最小的且比4大的数，即5(j位置)

④4与5交换，形成12543

⑤由于在此之前i的后序排列位递减序列，故交换后i的后序排列位递增序列

⑥对i后面的位数进行反转（4，33，4）形成最终排列12534

3.算法代码

void Reverse(int A[],int a,int b)//反转
{
while (a < b)
{
Swap(A[a], A[b]);
a++;
b--;
}
}
bool next_permutation(int A[], int n)
{
int i = n - 2;
while ((A[i + 1] <= A[i])&&i>=0)i--;
if (i<0)
{
Reverse(A,0,n-1);
return false;
}
else
{
int j = i+1;
while ((A[j] > A[i])&&j<n)j++;
Swap(A[j-1], A[i]);
Reverse(A ,i+1 , n-1);
return true;
}
}

注：当i<0时即该序列已经是最后的排列了，返回false并将序列变成最开始的排列（递增序列）

外部调用：

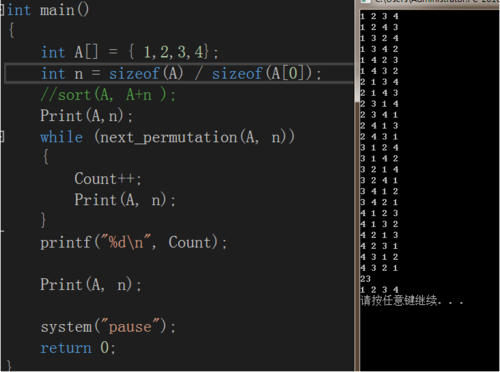
int main()
{
int A[] = { 1,2,3,4};
int n = sizeof(A) / sizeof(A[0]);
//sort(A, A+n );
Print(A,n);
while (next_permutation(A, n))
{
Count++;
Print(A, n);
}
printf("%d\n", Count);
 
Print(A, n);
 
system("pause");
return 0;
}

4.时间复杂度：单次查找时间复杂度为O(n)，列出所有全排列时间复杂度为O(n*n!)【遍历所有排列组合n!】+O(nlogn)【一开始的排序】

5.运行截图

注：当next_permutation返回false时即原排列已经处于递减序列了（最后一个），这时候返回的序列为递增序列（第一个）

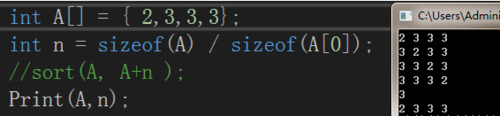
注：由于在位数筛选时不考虑等于的情况【while ((A[i + 1] <= A[i])&&i>=0)i--;】，否则将进入死循环（两位相等的数无限交换）

故此算法，若原序列中有重复项时并不会输出相同的排列。

6.STL模版函数：

在STL库algorithm文件中给出了此算法的官方模版函数next_permutation及prev_permutation

以下为源码：

next_permutation：
// TEMPLATE FUNCTION next_permutation
template<class _BidIt> inline
bool next_permutation(_BidIt _First, _BidIt _Last)
{// permute and test for pure ascending, using operator<
return (_STD next_permutation(_First, _Last, less<>()));
}
 
 
template<class _BidIt,
class _Pr> inline
bool next_permutation(_BidIt _First, _BidIt _Last, _Pr _Pred)
{// permute and test for pure ascending, using _Pred
_DEBUG_RANGE(_First, _Last);
return (_Next_permutation_unchecked(_Unchecked(_First), _Unchecked(_Last), _Pred));
}
 
 
// TEMPLATE FUNCTION next_permutation WITH PRED
template<class _BidIt,
class _Pr> inline
bool _Next_permutation_unchecked(_BidIt _First, _BidIt _Last, _Pr& _Pred)
{// permute and test for pure ascending, using _Pred
_BidIt _Next = _Last;
if (_First == _Last || _First == --_Next)       
return (false); //如果迭代器首尾相等或者等于尾地址-1返回false，用于边界安全。
 
for (; ; )
{// find rightmost element smaller than successor
_BidIt _Next1 = _Next;
if (_DEBUG_LT_PRED(_Pred, *--_Next, *_Next1))//找到i点
{// swap with rightmost element that's smaller, flip suffix
_BidIt _Mid = _Last;
for (; !_DEBUG_LT_PRED(_Pred, *_Next, *--_Mid); );//找到交换的j点
_STD iter_swap(_Next, _Mid);   //交换
_Reverse_unchecked(_Next1, _Last); //反序。
return (true);
}
 
 
//我们习惯于先把剪枝处理写在程序前面，而此算法这种情况只有一种（最后一个），
//不断地判断很浪费时间，还不如在最后再反回来。
if (_Next == _First)    //回到起点，即处于全排列最后一组的情况，再反回来并return false。
{// pure descending, flip all
_Reverse_unchecked(_First, _Last);
return (false);
}
}
}
 
// TEMPLATE FUNCTION reverse
template<class _BidIt> inline
void _Reverse_unchecked(_BidIt _First, _BidIt _Last)
{// reverse elements in [_First, _Last), bidirectional iterators
for (; _First != _Last && _First != --_Last; ++_First)
_STD iter_swap(_First, _Last);
}

prev_permutation同理

template<class _BidIt,
class _Pr> inline
bool prev_permutation(_BidIt _First, _BidIt _Last, _Pr _Pred)
{// reverse permute and test for pure descending, using _Pred
_DEBUG_RANGE(_First, _Last);
return (_Prev_permutation_unchecked(_Unchecked(_First), _Unchecked(_Last), _Pred));
}
 
// TEMPLATE FUNCTION prev_permutation
template<class _BidIt> inline
bool prev_permutation(_BidIt _First, _BidIt _Last)
{// reverse permute and test for pure descending, using operator<
return (_STD prev_permutation(_First, _Last, less<>()));
}
// TEMPLATE FUNCTION prev_permutation WITH PRED
template<class _BidIt,
class _Pr> inline
bool _Prev_permutation_unchecked(_BidIt _First, _BidIt _Last, _Pr& _Pred)
{// reverse permute and test for pure descending, using _Pred
_BidIt _Next = _Last;
if (_First == _Last || _First == --_Next)
return (false);
 
for (; ; )
{// find rightmost element not smaller than successor
_BidIt _Next1 = _Next;
if (_DEBUG_LT_PRED(_Pred, *_Next1, *--_Next))
{// swap with rightmost element that's not smaller, flip suffix
_BidIt _Mid = _Last;
for (; !_DEBUG_LT_PRED(_Pred, *--_Mid, *_Next); )
;
_STD iter_swap(_Next, _Mid);
_Reverse_unchecked(_Next1, _Last);
return (true);
}
 
if (_Next == _First)
{// pure ascending, flip all
_Reverse_unchecked(_First, _Last);
return (false);
}
}
}

7.参考文档

https://wenku.baidu.com/view/8c79a2facc17552706220880.html