亲和性巡礼第一站：局部性与内存缓存

此帖子不代表当前、过去或未来任何雇主的观点，文章中的观点纯属个人看法。

亲和力是一个如此迷人的主题！一方面，它是一个非常强大的概念，深入系统设计的核心，以实现优良性能；另一方面，特别是在出现问题时，它在调试时可能会非常棘手。至于定义，我打算稍微宽泛一点：

亲和度：倾向于使用相同资源处理相关对象的偏好

亲和力渗透到许多领域，有很多可谈的话题，自然而然，我们旅程的第一站就是局部性原理和内存缓存。让我们开始吧！

注：在物理学和计算机科学领域中，“局部性原则”是“The principle of locality”的常见翻译。

局部性原则，或称为引用局部性，对于性能而言至关重要。我甚至敢说，它可能比我一直钟爱的并行处理话题还要重要！这一原则源于程序常常重复使用最近访问过的数据。我们将给出一个更技术性的定义，如下所示：

局部性原则 ：处理器往往重复访问相同的内存位置。

有两种不同类型的地方性：时间局部性和空间局部性。时间局部性指的是最近被访问的数据在未来不久可能再次被访问。空间局部性指的是地址相近的数据可能在时间上也接近被访问。这可能就是“邻居”这个说法的由来。

那么局部性是如何发挥作用的呢？首先，我们需要来谈谈缓存及其层次结构。

内存缓存是一个临时数据存储区，用于加快对数据的访问速度。这些概念通过类比很容易理解，就好比…在一个我和我未来的妻子交往期间，她当时正在上计算机科学导论这门课，我用图书馆的例子来向她解释缓存层次结构的概念。她说她不记得了，但仍嫁给我了，所以我猜这应该是个不错的轶事吧（她笑着说）。

这个类比大致是这样的。“处理器”就像一个学生，而“内存访问”就是他们从一本书中读取页面。假设一个学生坐在桌前做作业。他们可能已经把需要的书打开到所需的页面，可以立即开始阅读——这是最快的内存访问，可能只需要几秒钟。学生可能在桌子上放了好几本书，他们可以在某个时刻切换到另一本书阅读。这大概需要几十秒，不过这没什么大不了的。到了某个时刻，他们需要的书不在桌子上，需要从书架上取书——哎呀，找书可能要花好几分钟，真是麻烦。但是如果需要的书根本就不在图书馆里呢？他们可能需要从存储中取出书，或者从另一个图书馆调书过来——现在我们谈论的是几个小时甚至几天的延迟！（希望他们早就开始做作业了，而且远远早于截止日期（希望他们早就开始做啦 :-)））

勤奋的学生会利用时间上的局部性和空间上的局部性。如果一名学生从书架上拿了一本书，他们可能会多次翻阅，直到获得所有需要的信息，然后才把书放回书架上——这就是时间上的局部性。同样，如果他们从书架上拿了一本书，不妨再顺手拿几本旁边关于同一主题的书，从而不必再回去取额外的书，节省了时间——这就是空间上的局部性。

计算机利用缓存层次结构来加快加载和存储操作的速度。缓存被分为不同的层级。零级缓存（L0）指的是CPU中的寄存器。一级缓存（L1）可能指的是每颗CPU上的SRAM缓存。二级缓存（L2）可能指的是由多个CPU共享的一块SRAM缓存。三级缓存（L3）可能由多个CPU和设备共享。RAM是系统的主存。在RAM之外，数据可以从如闪存驱动器或硬盘这样的存储设备中获取。

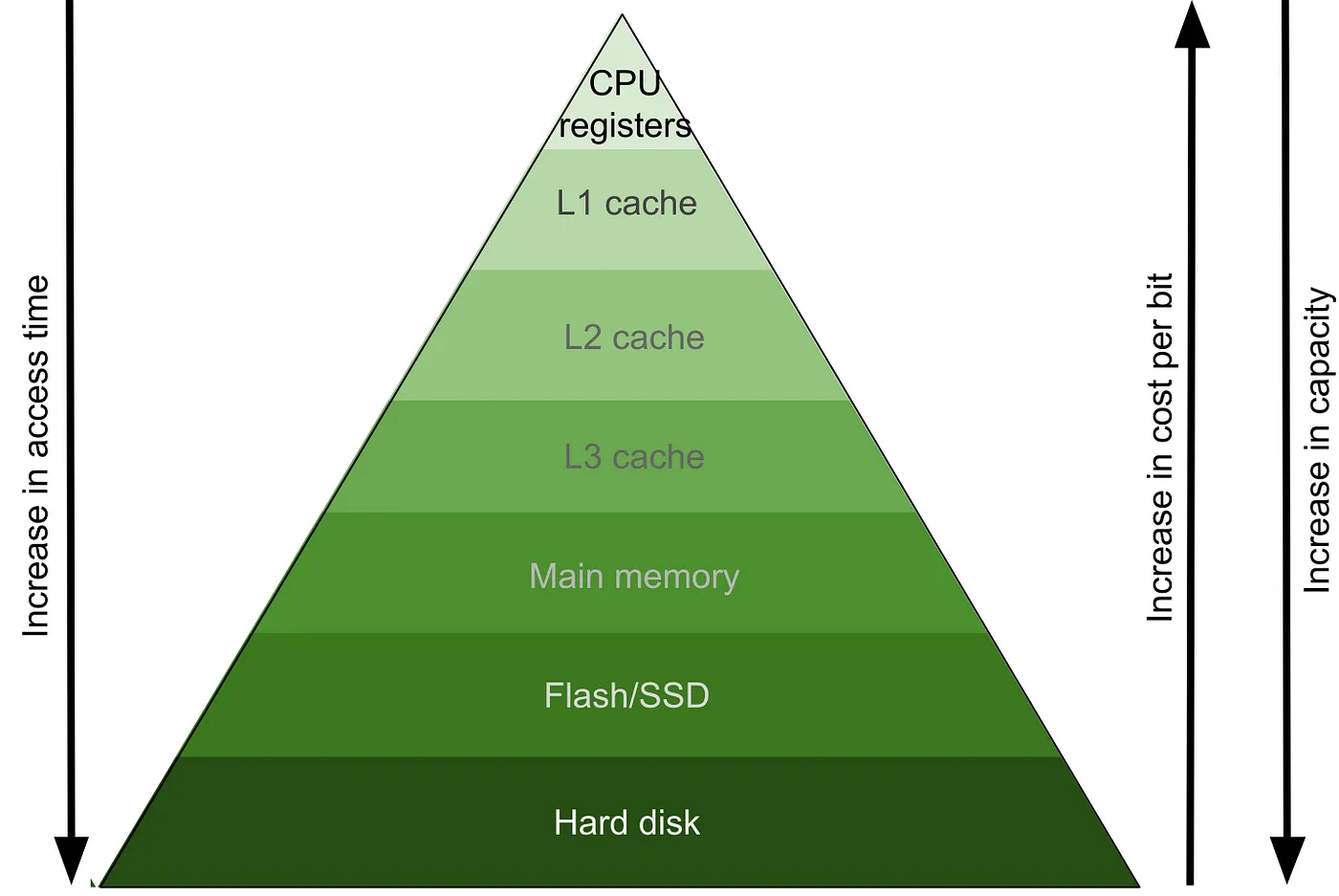
缓存层次结构。可以想象缓存层次结构就像一个金字塔。顶部靠近CPU，访问时间最快。往下移动金字塔，访问时间变长，但容量增大，成本减少。这就是缓存层次结构的基本概念。

在缓存层次结构中，不同的级别根据它们距离CPU的远近有不同的特性。

1. 距离CPU越近，访问速度越快。各级之间的访问时间可能相差一个数量级或更多。例如，学生在桌子上打开一本书和不得不走到书架上去找书之间的差异可能至少有10倍的时间。
2. 缓存是有限的，因此访问速度快通常意味着更昂贵的内存，内存容量也就相对较小。例如，桌子的空间只能放有限数量的书，与书架相比，这是非常有限的资源。
3. 距离CPU越近，内存的成本越高。快速访问速度是要付出代价的！比如，图书馆里的桌子每单位面积的成本可能比书架要高。

当缓存占满时会发生什么？在图书馆的类比中，书桌上的书会变得太多，如果学生想要从书架上拿一本新书，他们需要先归还一本书腾出空间。这引发了另一个有趣的问题：缓存中的哪些数据应该被淘汰？最常见的一种方法是最近最少使用（或称为LRU）。其思想是淘汰长时间没有被访问的数据，期望是处理器不再需要这些数据。

缓存性能与我们查找的数据是否在缓存中以及缓存的访问时间有关。如果我们找到的数据在缓存中，那么这就是一个“缓存命中”；如果数据不在缓存中，则是一个“未命中缓存”。在未命中缓存时，我们需要去缓存层次结构的下一层去寻找数据。这显然不是很好，因为比如图书馆的例子所示，当我们深入缓存层次结构去寻找所需数据时，成本和延迟会显著上升。

衡量缓存性能的一个指标是 缓存命中率（或类似的 缓存未命中率）。通常计算方法如下：

缓存命中率 (%) = 缓存命中数/缓存请求数

我们喜欢缓存命中率高，不喜欢命中率低。例如，如果一个缓存的命中率为90%，那么意味着90%的时间内它是快速内存访问，10%的时间内它是慢速访问。我们可以根据缓存命中率来估算访问时间。例如，如果L1缓存访问时间为10微秒，L2缓存访问时间为1000微秒，那么当缓存命中率为90%时，平均访问时间大约是：

0.9 乘以 10 微秒，加上 0.1 乘以 1000 微秒，等于 9 微秒 加上 100 微秒，等于 109 微秒

那么如果缓存命中率约为80%，大约的平均访问时间将是：

注意："大约的"在这里被添加以更精确地反映原文的不确定性，尽管这可能会使句子显得有些冗长。在实际应用中，可以考虑简化为"平均访问时间将是大约"或者"平均访问时间大约是"，以提高流畅度。

0.8 乘以 10 微秒 加上 0.2 乘以 1000 微秒 等于 208 微秒

你看，只要缓存命中率差10%，缓存访问时间就会几乎增加一倍。

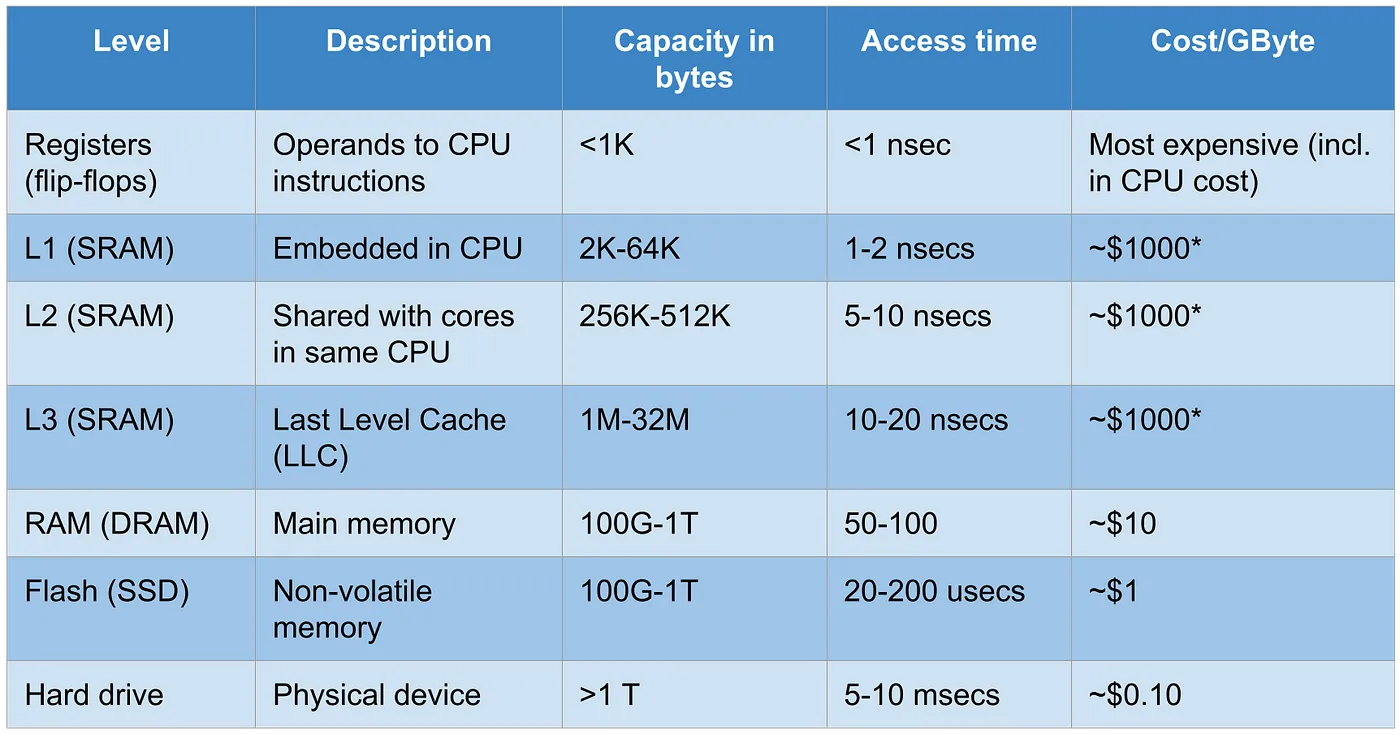
缓存层次结构的表格。这里列出了不同层次的缓存容量、访问时间和成本。请注意，L1到L3缓存（通常是SRAM）的成本较难确定，因为这些缓存集成在CPU内。

为什么缓存这么重要？这是因为缓存命中率和访问时间与程序运行时间密切相关。这也是程序员可以直接影响的部分。这时，时间和空间局部性的重要性就显现出来了。就像我们图书馆里勤奋的学生一样，程序员可以像勤奋的学生一样，通过保证内存访问具有空间和时间局部性，来缩短程序运行时间。

为了说明这个概念，让我们来看一个例子程序。在这里，我们只是初始化一个60000x60000字节的二维数组。需要总共3.6GB的内存，这个大小已经超过了L1到L3缓存的容量。我写了两个程序版本，分别称为 matrix1 和 matrix2 ：

    // matrix1.c  
    unsigned char matrix[60000][60000];  

    int main(int argc, char *argv[])  
    {  
            int i, j;  

            for (i = 0; i < 60000; i++)  
                    for (j = 0; j < 60000; j++)  
                            matrix[i][j] = 0;  
    }  

// matrix2.c
无符号字符矩阵[60000][60000];

int main(int argc, char *argv[])
{
        int i, j;

        for (i = 0; i < 60000; i++)
                for (j = 0; j < 60000; j++)
                        matrix[j][i] = 0;
}

它们之间唯一的不同在于赋值行。在 matrix1 中是 matrix[i][j] = 0，而在 matrix2 中则是 matrix[j][i] = 0。我只是将索引中的 i 和 j 互换了。也就是说，这么小小的改动能有多大差别呢？ :-) 我们来分别构建并运行这两个程序看看结果如何：

    tom@TomsPC:~/ctest$ gcc -o matrix1 matrix1.c  
    tom@TomsPC:~/ctest$ time ./matrix1  

    运行时间: 实测时间 0m6.100s  
    用户时间: 0m5.357s  
    系统时间: 0m0.740s

tom@TomsPC:~/ctest$ gcc -o matrix2 matrix2.c  
tom@TomsPC:~/ctest$ time ./matrix2  

实际用时 0m21.852s  
用户时间耗用 0m20.886s  
系统时间耗用 0m0.966s:  

所以 matrix1 用了 6.1 秒，而 matrix2 则用了 21.8 秒 —— 这意味着 matrix1 相比 matrix2 快了 3.57 倍。哇，差距真是挺大的！我们可以使用 Linux perf 工具来查看缓存未命中。

    tom@TomsPC:~/ctest$ perf stat -B -e cache-references,cache-misses,cycles,instructions,branches,faults,migrations ./matrix1  

     性能计数器统计数据为 './matrix1':  

            84,068,595      cache-references                                                        
            70,167,584      cache-misses                     # 占所有缓存引用的 83.46%           
        29,546,093,908      周期数                                                                  
        48,677,610,055      instructions                     # 每周期平均执行 1.65 条指令              
         4,554,588,175      分支数                                                                  
               878,961      faults                                                                  
                     1      migrations                                                              

           6.100422793 秒 流逝的总时间  

           5.336238000 秒 用户模式时间  
           0.764034000 秒 系统模式时间

    tom@TomsPC:~/ctest$ perf stat -B -e cache-references,cache-misses,cycles,instructions,branches,faults,migrations ./matrix2  

     性能计数器统计结果如下：  

        21,915,598,212      cache-references                                                        
         2,546,197,018      cache-misses                     #   11.62% 的所有缓存引用                                  
       107,497,287,135      cycles                                                                  
        48,771,658,896      instructions                     #    0.45 每周期指令数                                         
         4,569,254,812      总分支数                                                                
               878,960      faults                                                                  
                     8      migrations                                                              

          21.891134012 秒 耗时                                                    

          20.897737000 秒 用户耗时                                                    
           0.991940000 秒 系统耗时                                                 

当矩阵1运行时有7000万次缓存未命中，而矩阵2则有25亿次缓存未命中。bingo! 矩阵2运行起来慢多了，因为它有大量的缓存未命中——就像学生不断回到书架上拿新书一样！但是，为什么这个看似无害的改动会有如此大的影响呢？这是因为 矩阵1 具有很强的空间局部性，而 矩阵2 几乎没有。

内存被划分为缓存行（cache lines），这是缓存中存储的基本数据单元。例如，L1缓存通常有一个64字节的缓存行。当缓存未命中时，我们从主内存中加载整个缓存行，即使程序只是请求一个字节。这有助于空间局部性。如果程序访问了缓存行的第一个字节，那么它很可能会接着访问第二个、第三个等等。

让我们来看看 matrix1 和 matrix2 是如何与缓存互动的。首先，需要明白的是，赋值操作实际上是将某个地址处的字节设置为零。矩阵 matrix[i][j] 的内存地址是这样计算的：

基址矩阵 + i * 60000 + j

现在让我们来看看当 i = 2 时 matrix1 中的内部循环，并假设 matrix 的基地址为 135168（这个值是任意的，但为了内存对齐，它必须能被 64 整除）。如果我们稍微展开这个循环，将会得到类似以下这样的结果：

（此处省略具体的展开循环代码，因为原始文本中没有提供具体的代码示例。）

（注：省略的代码说明部分可以依据实际上下文进行补充。）

    matrix[2][0] = 0; // 设置位置 147168 的值为零
    matrix[2][1] = 0; // 设置位置 147169 的值为零
    matrix[2][2] = 0; // 设置位置 147170 的值为零
    ...

现在让我们做同样的事情，但把 i 和 j 在 matrix2 中换一下位置。这样我们就会得到：

    matrix[0][2] = 0; // 将该地址清零  
    matrix[1][2] = 0; // 将该地址清零  
    matrix[2][2] = 0; // 将该地址清零  
    ...

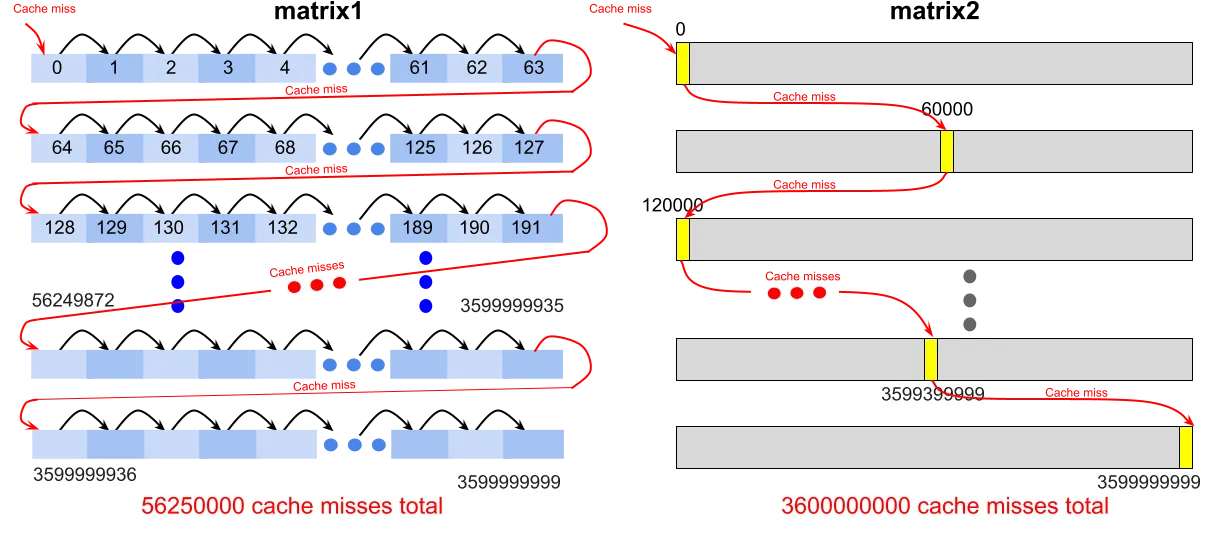
现在我们就能看出差别了。matrix1 每次循环迭代都访问连续的内存位置，这使得它具有空间局部性，因此它的缓存命中率很高。matrix2 则是跳来跳去，没有空间局部性，因此每次迭代都会缓存未命中的几率很高，缓存命中率很低。需要注意的是，在这个例子中，数据仅被访问了一次，因此，我们无需考虑时间局部性。

矩阵1和矩阵2程序中的缓存交互情况。左边显示，矩阵1程序以连续地址访问内存，因此具有很高的空间局部性，缓存未命中率相对较低（每六十四次访问中仅有一次未命中）。右边显示，矩阵2程序在内存中跳跃式访问地址，因此没有空间局部性，几乎每次访问都导致缓存未命中。请注意，预测的缓存未命中数并不完全反映来自perf的实际数据，这是由于缓存布局和策略的原因。

我们对缓存的描述只是触及皮毛。Hennessy 和 Patterson 的《计算机架构：定量方法》被公认为该领域的权威参考书。Patterson 和 Hennessy 的《计算机组织与设计》可能对普通读者来说稍微“不那么深入”，更适合初学者，并通过一个非常酷的矩阵乘法例子来详细说明，以展示局部性、并行性、向量指令和 GPU 的效果（这个例子非常贴切，因为线性代数在 AI 和机器学习中扮演着基础性角色）。