时间序列分析中的“制度转换模型”详解及Python实现

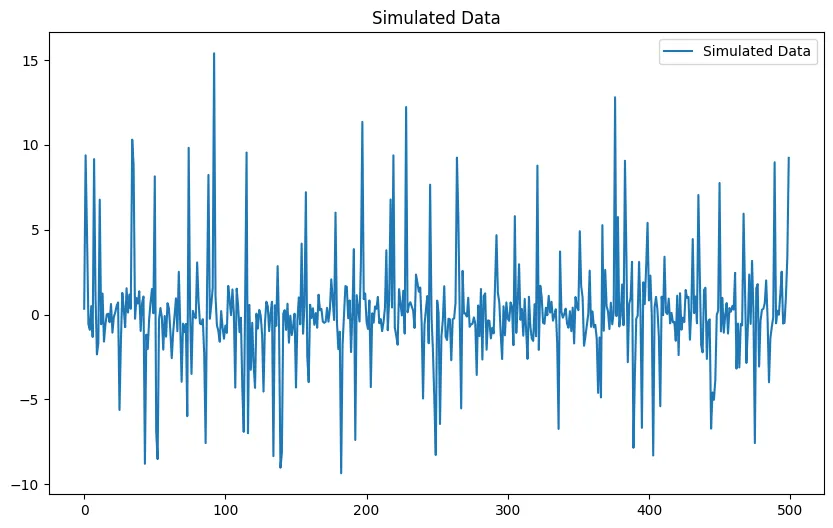
我们在不同时间间隔的时间序列数据中寻找模式。例如，股票市场在危机期间可能表现出高波动性，在稳定期间则波动性较低。切换制度模型通过假设时间序列在不同的“制度”之间切换来识别这种行为，每个制度都有自己独特的统计特性。

在这篇文章中，我们将探讨制度切换模型、它们的应用场景以及如何在 Python 中使用 statsmodels 库实现它们。

由詹姆斯·汉密尔顿在1989年引入的 regime switching（动态转换）模型通过允许在不同的状态之间转换来捕捉时间序列数据中的结构变化。这些模型特别适用于以下情况：

1. 经济学：模拟经济的衰退和扩张周期。
2. 金融：分析牛市和熊市。
3. 能源：监测需求或生产趋势的变动。
4. 天气：捕捉天气状态的变化。

最常见的一种制度转换模型是马尔可夫切换模型，其中的切换是按照马尔可夫过程进行的。

马尔可夫切换模型就像是一个会讲故事的人，知道同一个故事的多个版本。想象一下，经济像是在繁荣和萧条之间跳来跳去。在任意时刻，经济是否处于状态A（繁荣）或状态B（萧条），这取决于当前的时期。比如，状态A可能是经济增长迅速的时期，而状态B可能是经济放缓或衰退的时期。

这种神奇的效果就是马尔可夫链的运作，其中下一个状态只依赖于当前状态，而不依赖于过去的状态。可以把它想象成天气预报——明天的天气主要看今天的天气，而不是上周怎么样了。从一个状态转换到另一个状态的概率（转换概率）在每个当前状态下都是固定的。比如，在繁荣期，有 90% 的几率保持繁荣，10% 的几率转为萧条。

在每个状态内，结果遵循特定于该状态的概率分布（状态依赖概率）。在繁荣时期，增长平均为3%，并且波动性较低；而在衰退时期，增长平均为-1%，并且波动性较高。该模型结合了这些元素——状态识别、转换概率以及特定于状态的行为——以捕捉数据中的复杂模式和特征。

statsmodels库通过其MarkovRegression和MarkovAutoregression类提供了一种方便的实现来实现马尔可夫切换模型。我们通过一个例子来说明。

    import numpy as np  # 导入 numpy 作为 np，这是用于数值计算的库  
    import pandas as pd  # 导入 pandas 作为 pd，这是用于数据处理和分析的库  
    import matplotlib.pyplot as plt  # 导入 matplotlib.pyplot 作为 plt，这是用于绘图的库  
    from statsmodels.tsa.regime_switching.markov_regression import MarkovRegression  # 从 statsmodels.tsa.regime_switching.markov_regression 导入 MarkovRegression，这用于马尔可夫回归分析  
    import seaborn as sns  # 导入 seaborn 作为 sns，这是一个用于统计图形绘制的库  
    from scipy import stats  # 从 scipy 导入 stats，这是用于统计计算的库

我们将生成高低波动性两种合成数据。

    # 生成并准备数据  
    np.random.seed(42)  
    n = 500  
    模式 = np.random.choice([0, 1], size=n, p=[0.7, 0.3])  
    数据 = np.array(np.random.normal(0, np.where(模式 == 0, 1, 5)))  

    # 2. 创建数据框，包含所有信息  
    df = pd.DataFrame({  
        '数据': 数据,  
        '真实模式': 模式,  
        '时间': range(n)  
    })

    # 拟合马尔可夫切换模型如下:
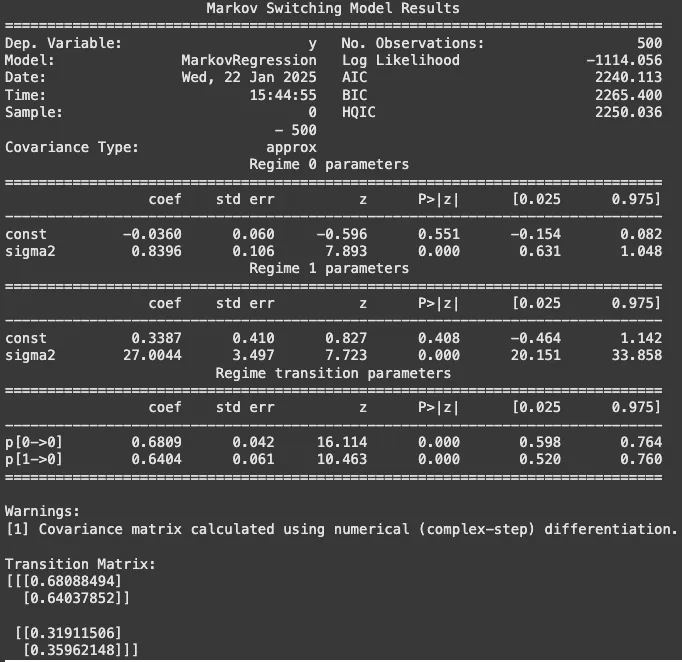
    model = MarkovRegression(data, k_regimes=2, trend='常数', switching_variance=True)  
    result = model.fit()  
    print(result.汇总())  

    print("\n转换矩阵如下:")  
    print(result.状态转换)

现在我们已经得到了每个点的实测数据和预测数据。

    # 添加高概率预测和状态标签到DataFrame  
    df['高概率预测'] = result.smoothed_marginal_probabilities[:, 1]  
    df['预测状态标签'] = np.argmax(result.smoothed_marginal_probabilities, axis=1)  

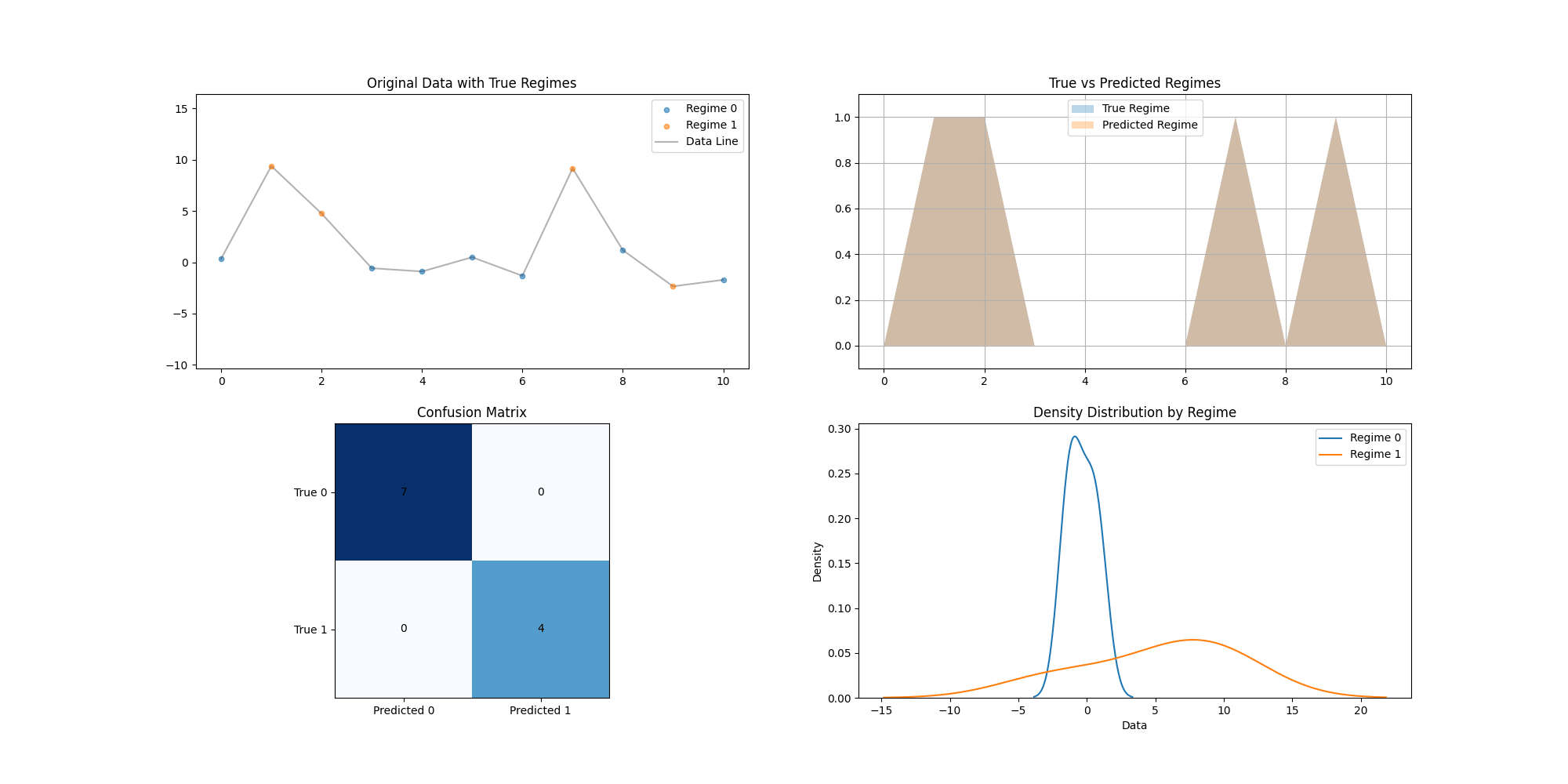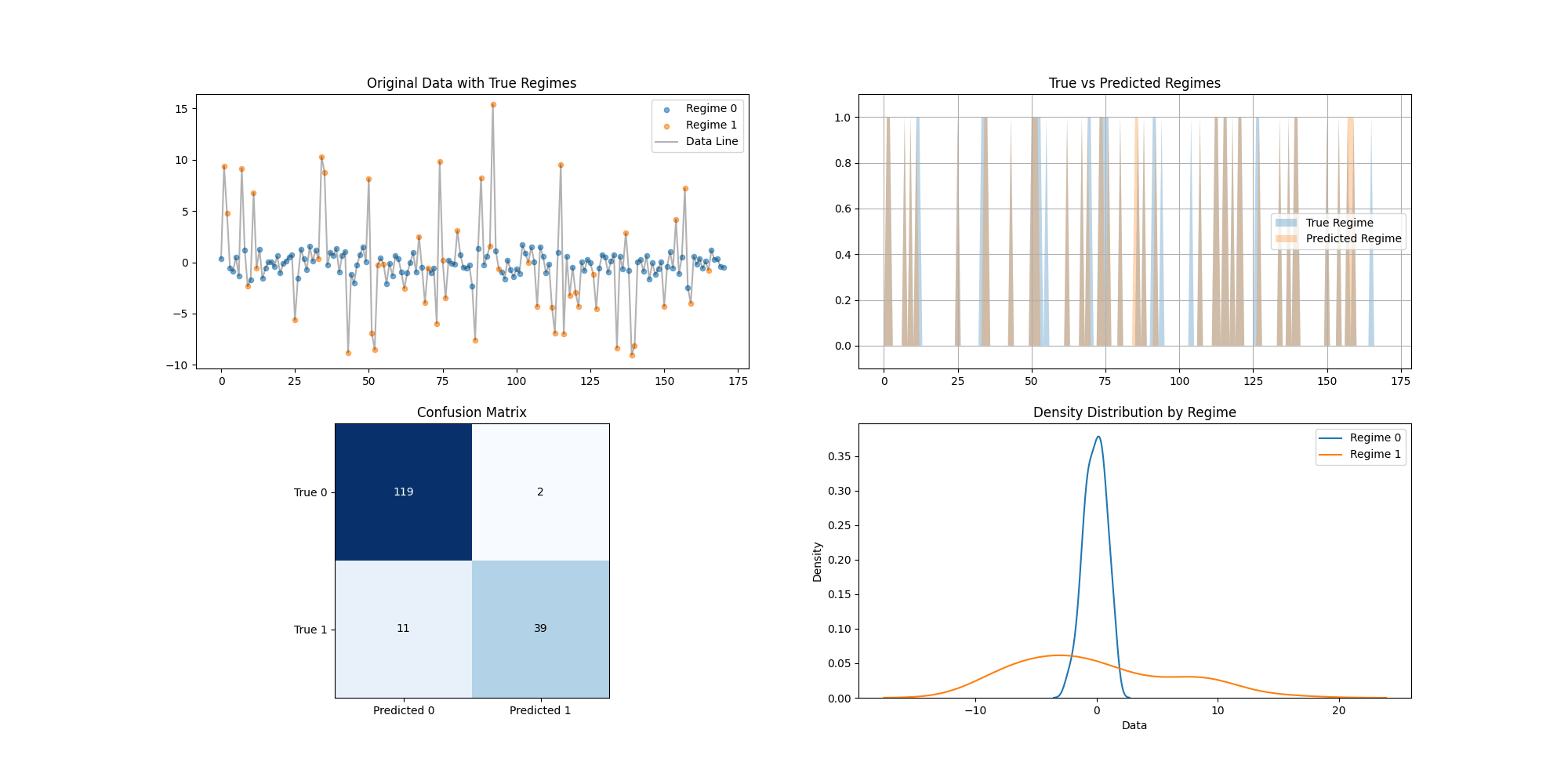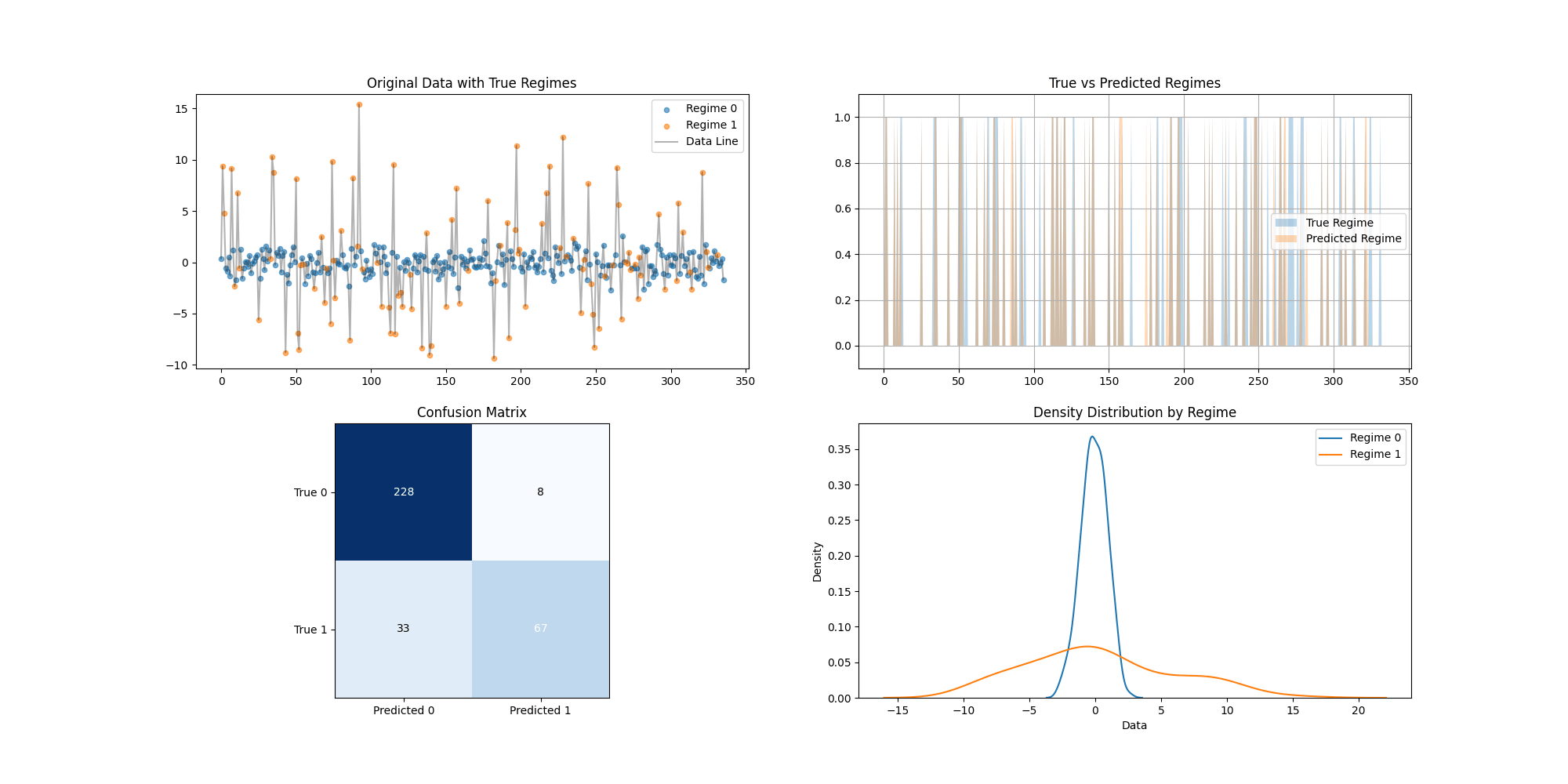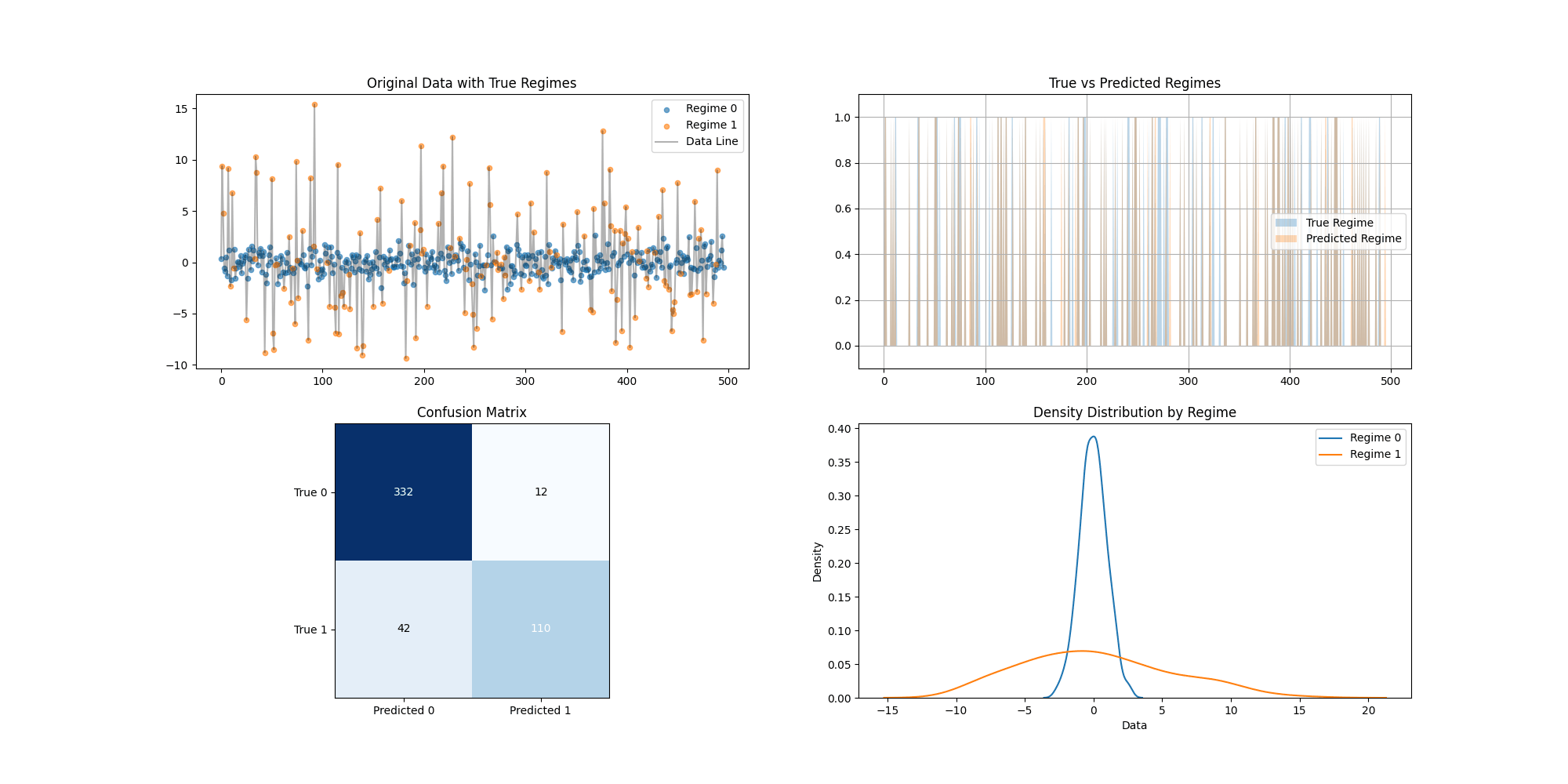
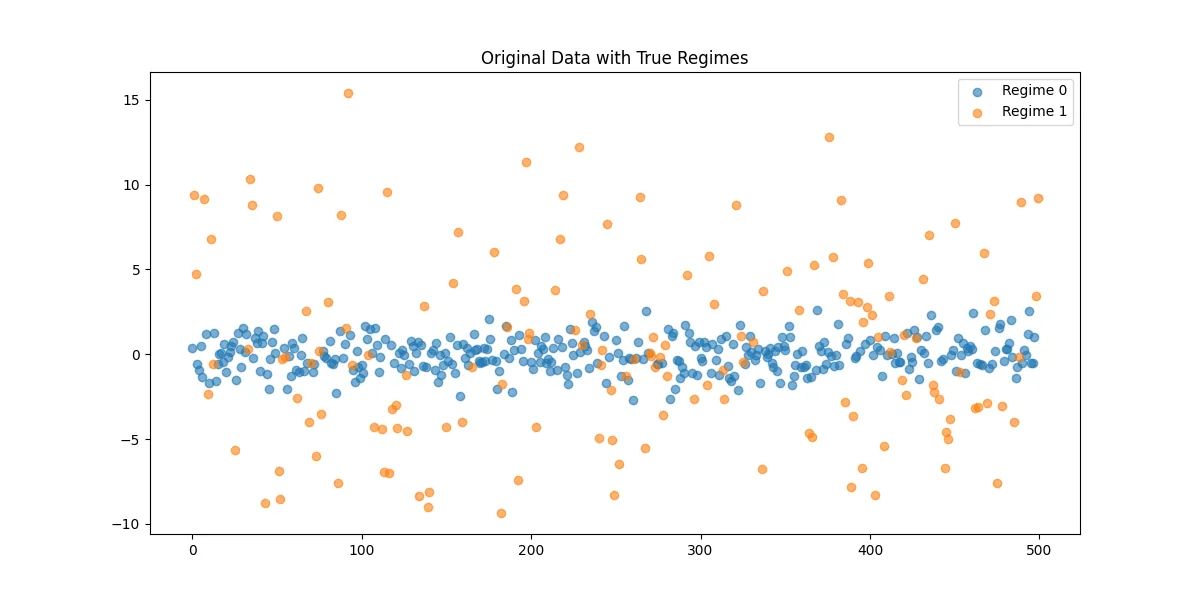
    # 图1：原始数据及其真实状态  
    plt.figure(figsize=(12, 6))  
    for 状态标签 in [0, 1]:  
        mask = df['真实状态'] == 状态标签  
        plt.scatter(df[mask]['Time'], df[mask]['Data'],  
                    label=f"状态标签 {状态标签}", alpha=0.6)  
    plt.title("原始数据及其真实状态")  
    plt.legend()  
    plt.savefig('原始数据及其状态.png')  
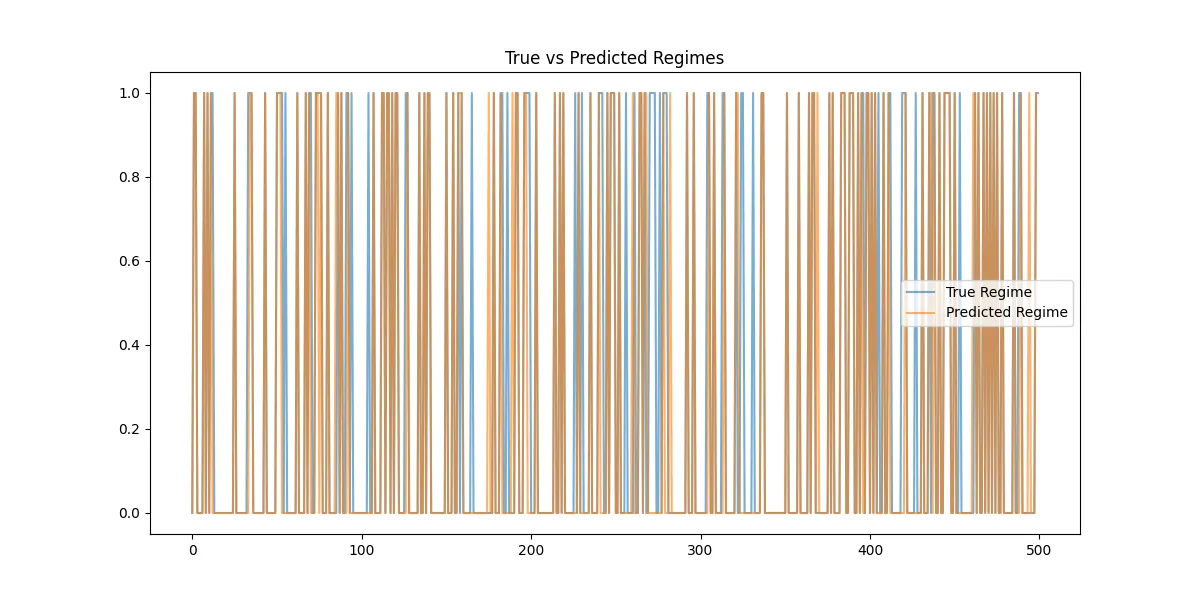
    plt.close()

    # 图 2：预测体制与真实体制对比  
    plt.figure(figsize=(12, 6))  
    plt.plot(df['True_Regime'], label='真实体制', alpha=0.6)  
    plt.plot(df['Predicted_Regime'], label='预测体制', alpha=0.6)  
    plt.title("真实体制与预测体制对比")  
    plt.legend()  
    plt.savefig('true_vs_predicted_regimes.png')  
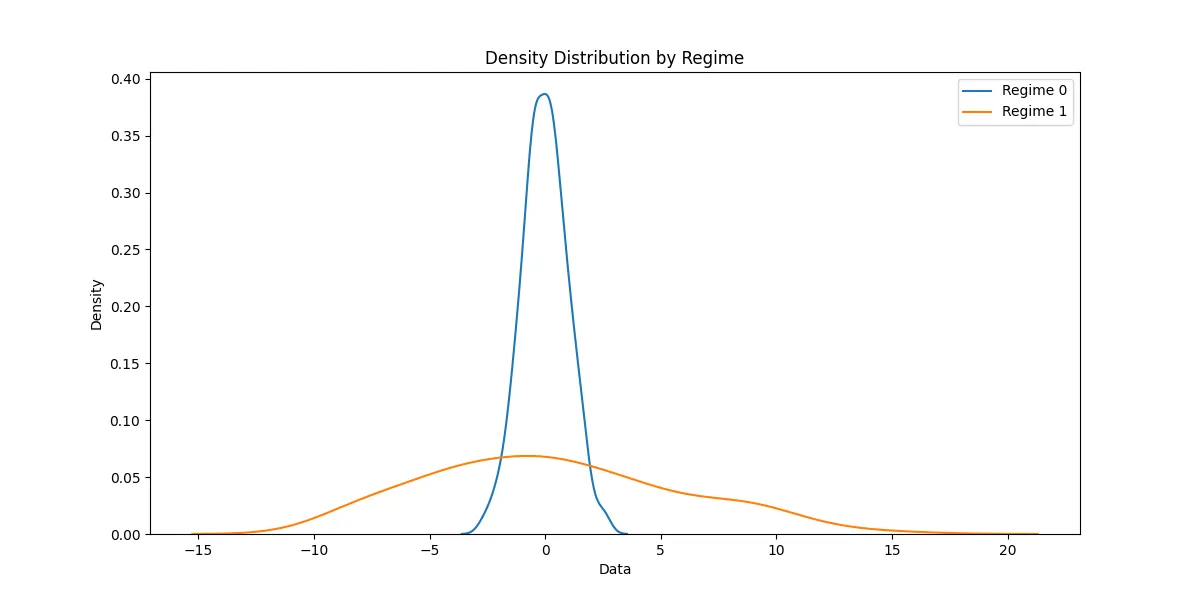
    plt.close()

    # 绘制每个状态的密度图  
    plt.figure(figsize=(12, 6))  
    for 状态 in [0, 1]:  
        sns.kdeplot(data=df[df['True_Regime'] == 状态]['Data'],   
                    label=f"状态 {状态}")  
    plt.title("各状态下的数据密度分布")  
    plt.legend()  
    plt.savefig('density_distribution.png')  
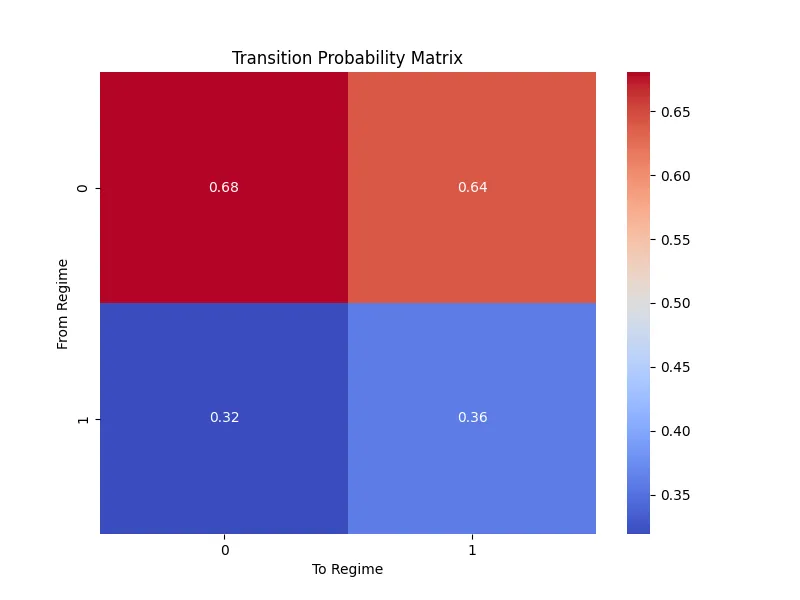
    plt.close()

    # 绘制转换概率矩阵热力图  
    plt.figure(figsize=(8, 6))  
    转移矩阵 = result.regime_transition.reshape(2, 2)  
    sns.heatmap(转移矩阵, annot=True, cmap='coolwarm')  
    plt.title("转移概率矩阵")  
    plt.xlabel("转入状态")  
    plt.ylabel("转出状态")  
    plt.savefig('transition_matrix.png')  
    plt.close()

    # 图5：模型性能指标  
    plt.figure(figsize=(8, 6))  
    混淆矩阵图 = pd.crosstab(df['True_Regime'], df['Predicted_Regime'])  
    sns.heatmap(混淆矩阵图, annot=True, fmt='d', cmap='Blues')  # 混淆矩阵图展示
    plt.title("混淆矩阵：真实体制 vs 预测体制")  
    plt.xlabel("预测体制")  
    plt.ylabel("真实体制")  
    plt.savefig('confusion_matrix.png')  # 保存混淆矩阵图
    plt.close()  # 关闭当前图像窗口

    # 输出统计信息  
    print("\n模型性能指标如下:")  
    accuracy = (df['True_Regime'] == df['Predicted_Regime']).mean()  
    print(f"预测准确度: {accuracy:.2%}")  

    print("\n状态模式统计信息:")  
    for regime in [0, 1]:  
        regime_data = df[df['True_Regime'] == regime]['Data']  
        print(f"\n状态模式 {regime}:")  
        print(f"均值: {regime_data.mean():.2f}")  
        print(f"标准偏差: {regime_data.std():.2f}")  
        print(f"偏度: {stats.skew(regime_data):.2f}")  
        print(f"峰度: {stats.kurtosis(regime_data):.2f}")  

    print("\n各状态模式的平均持续时间:")  
    for regime in [0, 1]:  
        regime_runs = (df['Predicted_Regime'] == regime).astype(int).groupby(  
            (df['Predicted_Regime'] != df['Predicted_Regime'].shift()).cumsum()  
        ).sum()  
        print(f"状态模式 {regime}: {regime_runs.mean():.2f} 个周期")  

    # 计算并输出转换统计信息  
    transitions = pd.DataFrame({  
        '从': df['Predicted_Regime'][:-1],  
        '到': df['Predicted_Regime'][1:]  
    })  
    print("\n转换统计信息表:")  
    print(pd.crosstab(transitions['从'], transitions['到']))

在拟合切换状态模型之前，我们需要确保数据是平稳的，这可以通过使用DF检验或KPSS检验来完成。我们还需要定义我们认为数据中存在的状态的数量，这可以基于专业知识或通过最大化AIC值来确定。

或

总结

制度切换模型为分析时间序列中的结构性变化提供了一个灵活的框架。它们能帮助我们发现传统模型可能忽视的关键点。你可以用Python和statsmodels高效实现这些模型，并根据具体需求灵活调整。

用于提升预测准确性的特定于某种制度的模型。可以用来发现显著的时间序列变化点，以识别时间序列行为中的变化点。

状态切换也可以用于时间序列分类或聚类中的特征工程，以便为后续的ML任务准备数据。