用户上传的图片
这个系列是讲什么的?欢迎来到我的系列教程的第二部分,内容是营销组合模型(MMM)。这是一份实用指南,帮助你更好地理解和掌握MMM。在本系列中,我们将探讨模型训练、验证、校准和预算优化等关键问题,全部使用强大的pymc-marketing Python库。无论你是MMM的新手还是想提升技能的老手,本系列将为你提供实用工具和见解,帮助你优化营销策略。
如果你错过了第一集,可以在这里看下:
用Python掌握营销组合模型Part 1 一步步教你精通Python中MMM的实战指南 简介在这一系列的第二部分中,我们将集中讨论使用实验数据校准模型。
- 为什么校准营销组合模型很重要?
- 我们怎样利用贝叶斯先验值来校准我们的模型?
- 我们可以运行哪些实验来帮助我们确定贝叶斯先验值?
我们将用 Python 和 pymc-marketing 包来完成这个模型的校准,作为结尾。这个模型是在我们之前的第一篇文章里构建的。
你可以在这里查看完整的笔记。
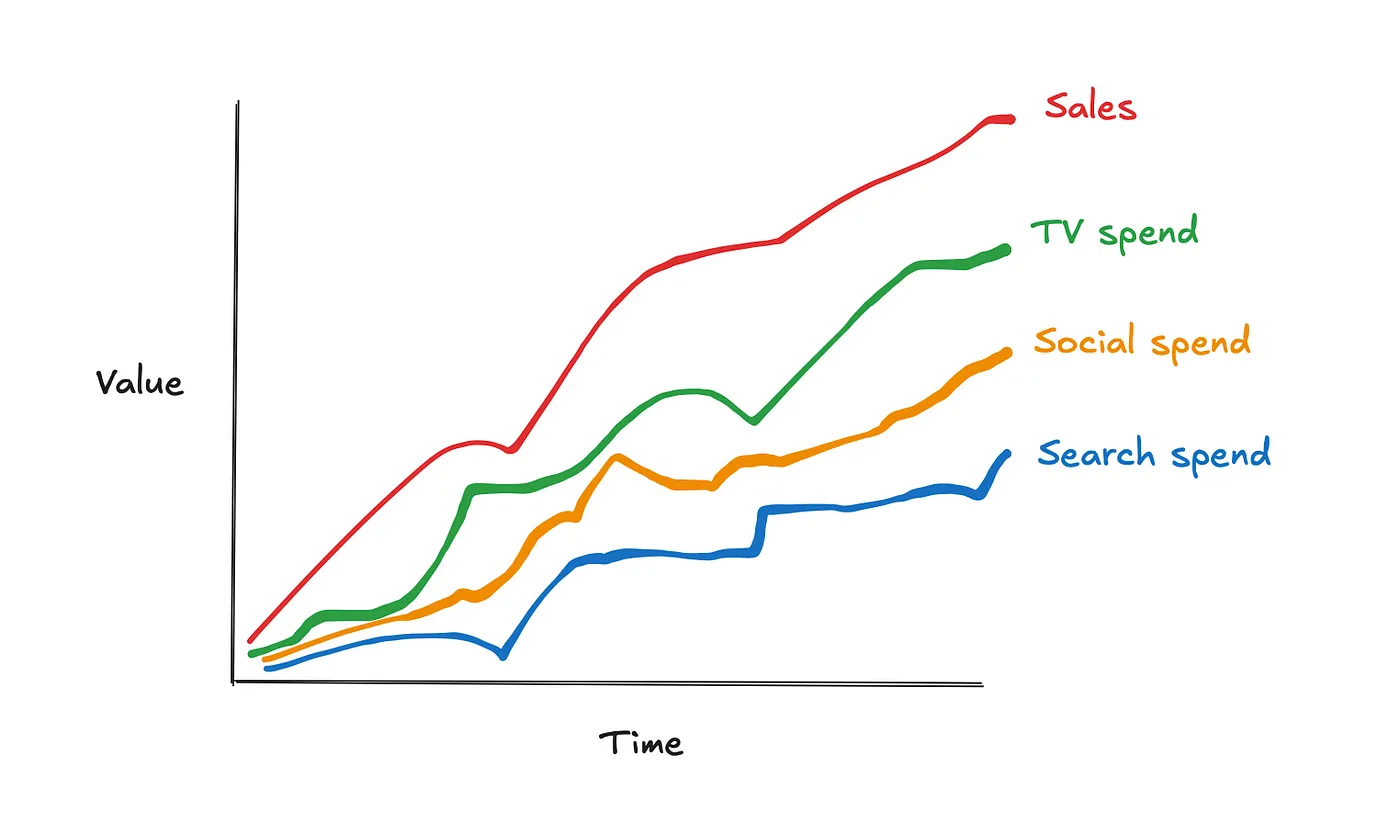
pymc_marketing/notebooks/2. 调整营销组合模型(MMM)(Python.ipynb)在主分支·…这里有一个使用pymc_marketing包演示MMM的例子。通过在github上创建账户参与raz1470/pymc_marketing的项目 1.0 校准营销组合模型。营销组合模型(MMM)是一种统计技术,用于评估不同营销渠道(如电视广告、社交媒体、付费搜索)对销售的效果。MMM旨在了解每个渠道的投资回报率(ROI),并优化未来的营销预算。
有几个原因我们要调整模型。在我们开始Python实操之前,简单聊聊这些原因。
1. 1 为什么调整营销组合模型很重要呢?校准MMM非常重要,因为虽然它们提供了很多有用的见解,但仍受到很多因素的限制。
- 多重共线性: 当不同的营销渠道之间高度相关时,就会发生这种情况,使得难以区分它们各自的效应。例如,电视和社交媒体可能同时运行,导致它们影响的重叠。校准通过引入额外的数据或限制条件,帮助我们理清这些渠道的影响。
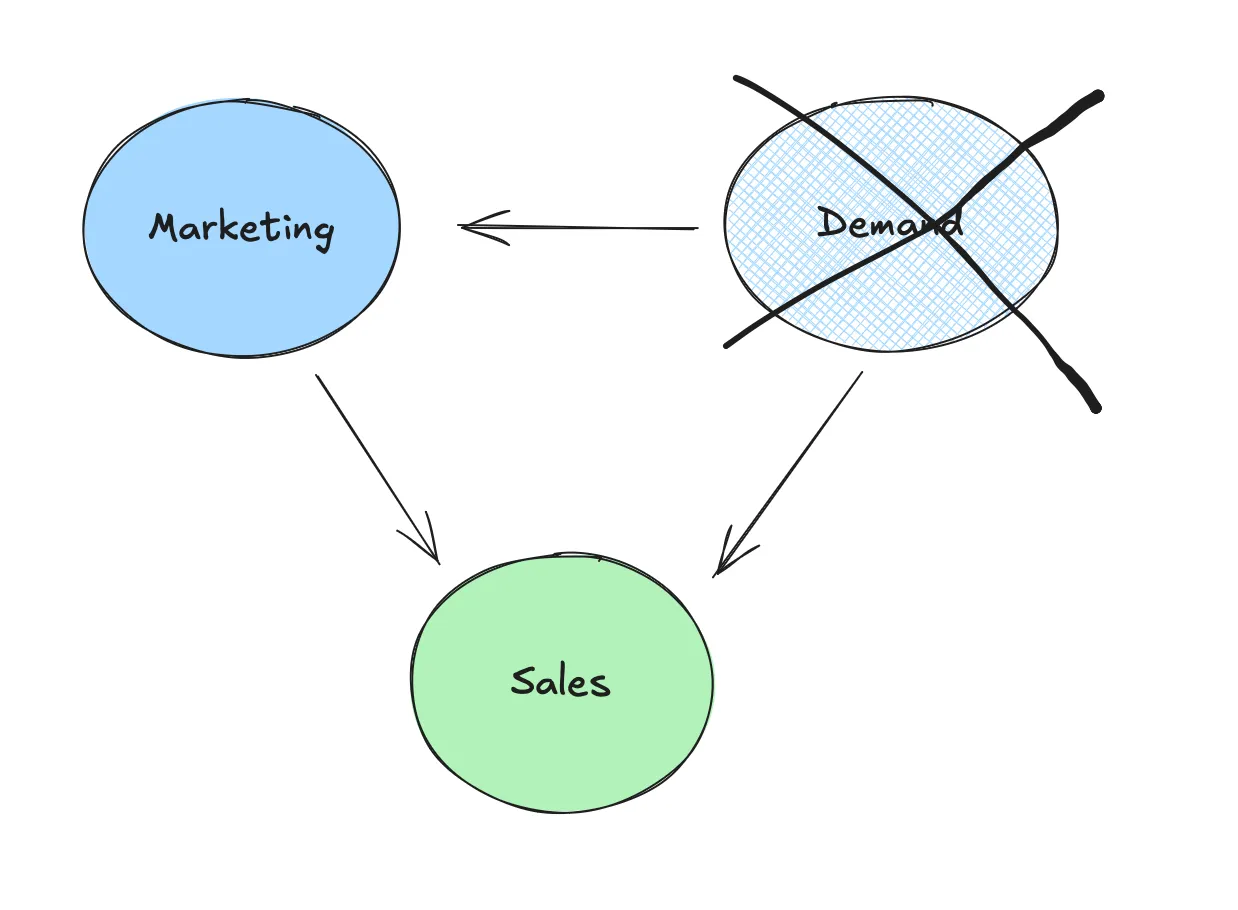
- 未观测到的干扰因素: MMM 模型依赖于观察到的数据,但可能会遗漏一些重要变量,这些变量同样会影响营销和销售,例如季节性或市场需求的变化。校准可以帮助我们纠正这些未被注意到的影响因素。
用户使用excalidraw绘制的图像(excalidraw,一个绘图工具)
- 重新定位的偏误: 你有没有访问过某个产品的网站,然后发现你的所有社交媒体平台突然“巧合地”开始向你展示该产品的广告?这其实是有意为之,我们称这种现象为“重新定位”,并且有时确实能起到效果。事实上,很多被重新定位的潜在客户本就会购买,即使不进行重新定位。
如果没有正确的校准,这些问题可能会导致对营销渠道效果的不准确估计,从而在营销支出和策略的决策上出现失误。
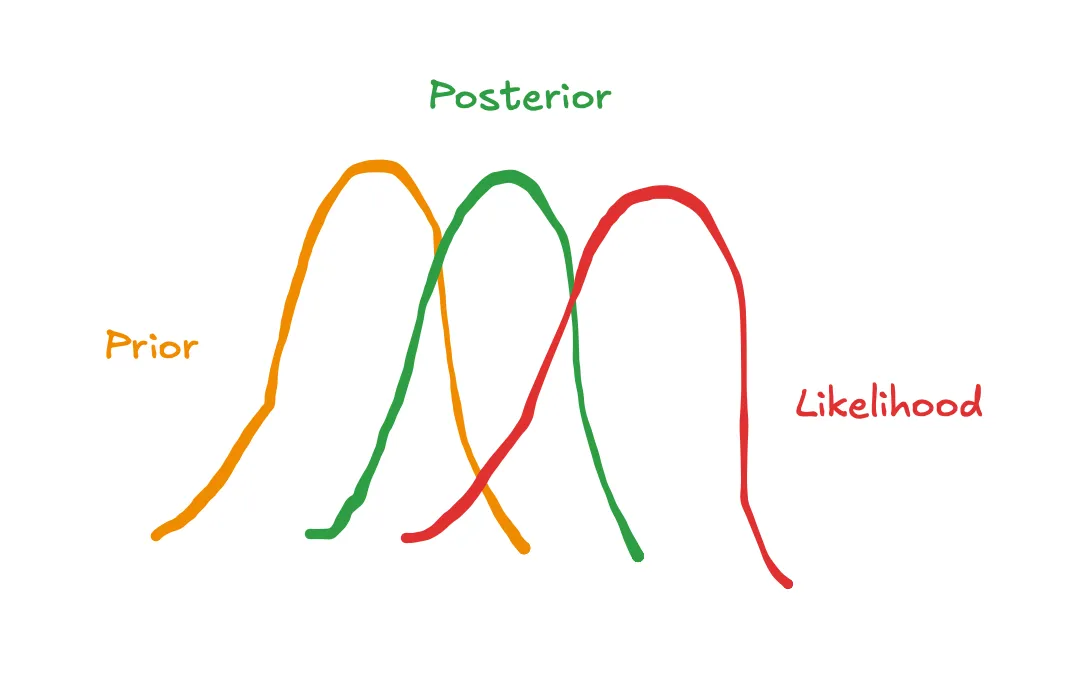
1.2 我们怎么用贝叶斯先验来调整我们的模型呢?在上一篇文章里,我们讨论了如何用贝叶斯先验表示我们对模型参数的初始信念,例如电视广告支出对销售额的影响力。我们还介绍了pymc-marketing中的默认参数是合理但信息量较弱的选择。提供基于实验的更有信息量的先验可以帮助我们校准模型,并解决上一节提出来的问题。
用户生成的图片(来自Excalidraw)
在 pymc-marketing 中,有几种方法可以设定先验。
- 可以直接像下面的例子这样做,更改默认的饱和度_beta先验,使用截断的正态分布来限制值为正值。请注意,'saturation_beta' 保留英文,因为它看起来像是特定的变量名或参数名。
model_config = {
'intercept': Prior("Normal", mu=0, sigma=2),
'likelihood': Prior("Normal", sigma=Prior("HalfNormal", sigma=2)),
'gamma_control': Prior("Normal", mu=0, sigma=2, dims="control"),
'gamma_fourier': Prior("Laplace", mu=0, b=1, dims="fourier_mode"),
'adstock_alpha': Prior("Beta", alpha=1, beta=3, dims="channel"),
'saturation_lam': Prior("Gamma", alpha=3, beta=1, dims="channel"),
'saturation_beta': Prior("TruncatedNormal", mu=[0.02, 0.04, 0.01], lower=0, sigma=0.1, dims=("channel"))
}
mmm_with_priors = MMM(
model_config=model_config,
adstock=GeometricAdstock(l_max=8),
saturation=LogisticSaturation(),
date_column=date_col,
channel_columns=channel_cols,
control_columns=control_cols,
)- 使用
add_lift_test_measurements这个方法,该方法向模型中添加一个新的概率项,有助于校准饱和度曲线,我们会在后续的 Python 教程中详细讲解这一点。
如果你对贝叶斯分析感到不自在,你的替代方案是使用像cvxpy这样的软件包运行带约束的回归作为一种替代方案。下面是一个使用变量系数的上下限来进行约束回归的例子:
import cvxpy as cp
def train_model(X, y, reg_alpha, lower_bounds, upper_bounds):
"""
训练一个带有L2正则化(岭回归)和系数边界约束的线性回归模型。
参数:
-----------
X : numpy.ndarray 或类似
特征矩阵,每一行代表一个观测值,每一列代表一个特征。
y : numpy.ndarray 或类似
回归的目标变量。
reg_alpha : float
岭惩罚项的正则化强度。较高的值会更严厉地惩罚较大的系数值。
lower_bounds : 浮点数列表或None
模型中每个系数的下界。如果某个系数没有下界,则将其设置为None。
upper_bounds : 浮点数列表或None
模型中每个系数的上界。如果某个系数没有上界,则将其设置为None。
返回:
--------
numpy.ndarray
回归模型的拟合系数数组。
示例:
--------
>>> coef = train_model(X, y, reg_alpha=1.0, lower_bounds=[0.2, 0.4], upper_bounds=[0.5, 1.0])
"""
coef = cp.Variable(X.shape[1])
ridge_penalty = cp.norm(coef, 2)
objective = cp.Minimize(cp.sum_squares(X @ coef - y) + reg_alpha * ridge_penalty)
# 基于提供的边界创建约束条件
constraints = (
[coef[i] >= lower_bounds[i] for i in range(X.shape[1]) if lower_bounds[i] is not None] +
[coef[i] <= upper_bounds[i] for i in range(X.shape[1]) if upper_bounds[i] is not None]
)
# 定义并求解该问题
problem = cp.Problem(objective, constraints)
problem.solve()
# 打印优化状态信息
print(problem.status)
return coef.value实验可以提供有力的证据来帮助确定MMM中使用的先验。比如,一些常见的实验包括:
(注:MMM即多模式模型(Multi-Modal Model))
用户生成的图片(excalidraw)
- 转化率提升测试 — 这些测试通常在Facebook、YouTube、Snapchat、TikTok和DV360等平台上进行,用户被随机分为测试组和对照组。测试组会接触到营销活动,而对照组不会。通过两组之间转化率的差异,可以评估渠道的实际提升效果。
- 地域提升测试 — 在地域提升测试中,某些地理区域暂停营销活动,而其他区域继续进行。通过对比测试区域和对照区域的表现,可以衡量每个区域营销活动的增量影响。CausalPy Python库提供了一个易于使用的方法,非常值得尝试:
- 切换测试 — 这种方法就是在短时间内快速开启和关闭营销活动,来观察消费者行为的变化。这种方法最适用于那些能立即产生效果的渠道,例如付费搜索。
通过这些实验,你可以获得强有力的实证数据来完善你的贝叶斯先验分布,并进一步提高市场组合模型的准确性和校准。
Python入门指南 2.0现在我们知道了为什么需要校准模型,现在我们来校准一下第一篇文章里的那个模型吧。下面我们就来看看具体步骤。
- 模拟数据
- 模拟实验
- 预处理实验数据
- 调整模型
- 验证模型的有效性
我们将从模拟第一篇文章中的数据开始。如果你想了解更多关于数据生成方式的信息,请查看第一篇文章,我们在那里进行了详细的介绍。
精通Python中的营销组合模型第一部分手把手教你精通MMM的实战指南towardsdatascience.com当我们训练第一篇文章中的模型时,电视广告、社交媒体和搜索引擎的贡献都被高估了。这似乎是由代理需求没有真正需求那么大所驱动的。所以让我们接着上次的工作继续,想想怎么通过实验来解决这个问题。
2.2 模拟实验为了模拟某些实验结果,我们编写了一个函数,该函数接收已知的通道参数并输出该通道的真实贡献。请记住,在实际情况下我们无法得知这些参数,但这个练习将帮助我们测试并理解来自pymc-marketing的校准流程。
def exp_generator(起始日期, 时期数, 渠道, adstock_alpha, saturation_lamda, beta, 每周支出, 最大绝对支出, 频率="W"):
"""
生成包含广告积压效应和饱和效应的实验结果时间序列。
参数:
----------
起始日期 : str 或 datetime
时间序列的起始日期。
时期数 : int
生成的时间序列中的时期数量(例如,周数)。
渠道 : str
营销渠道的名称。
adstock_alpha : float
广告积压衰减率,范围在0到1之间。
saturation_lamda : float
饱和参数(lambda)。
beta : float
beta系数。
每周支出 : float
渠道的每周原始支出金额。
最大绝对支出 : float
用于标准化支出数据的最大绝对支出值,使序列在0到1之间进行归一化。
频率 : str,可选
时间序列的频率,默认为 'W' 表示每周。遵循 pandas 偏移别名。
返回:
-------
df_exp : pd.DataFrame
包含生成的时间序列的DataFrame,包含以下列:
- 日期 :序列中的每个时期日期。
- {渠道}_支出原始 :渠道的原始每周支出。
- {渠道}_支出 :通过 `最大绝对支出` 标准化的渠道支出。
- {渠道}_广告积压 :根据 `adstock_alpha` 进行时间衰减的广告积压转换支出。
- {渠道}_逻辑饱和 :应用 `saturation_lamda` 逻辑饱和后的广告积压转换支出。
- {渠道}_销售 :计算为饱和支出乘以 `beta` 的销售贡献。
示例:
--------
>>> df = exp_generator(
... 起始日期="2023-01-01",
... 时期数=52,
... 渠道="电视渠道",
... adstock_alpha=0.7,
... saturation_lamda=1.5,
... beta=0.03,
... 每周支出:50000,
... 最大绝对支出=1000000
... )
"""
# 0. 创建时间维度
日期范围 = pd.date_range(start=起始日期, periods=时期数, freq=频率)
df_exp = pd.DataFrame({'日期': 日期范围})
# 1. 创建原始渠道支出
df_exp[f"{渠道}_支出原始"] = 每周支出
# 2. 标准化渠道支出
df_exp[f"{渠道}_支出"] = df_exp[f"{渠道}_支出原始"] / 最大绝对支出
# 3. 应用广告积压转换
df_exp[f"{渠道}_广告积压"] = geometric_adstock(
x=df_exp[f"{渠道}_支出"].to_numpy(),
alpha=adstock_alpha,
l_max=8, normalize=True
).eval().flatten()
# 4. 应用逻辑饱和转换
df_exp[f"{渠道}_逻辑饱和"] = logistic_saturation(
x=df_exp[f"{渠道}_广告积压"].to_numpy(),
lam=saturation_lamda
).eval()
# 5. 计算销售贡献
df_exp[f"{渠道}_销售"] = df_exp[f"{渠道}_逻辑饱和"] * beta
return df_exp下面我们就用这个功能来生成一个为期8周的电视增肌测试的结果。
# 设置实验生成器所需的参数如下
start_date = "2024-10-01"
periods = 8
channel = "tv"
adstock_alpha = adstock_alphas[0]
saturation_lamda = saturation_lamdas[0]
beta = betas[0]
weekly_spend = df['tv_spend_raw'].mean()
max_abs_spend = df['tv_spend_raw'].max()
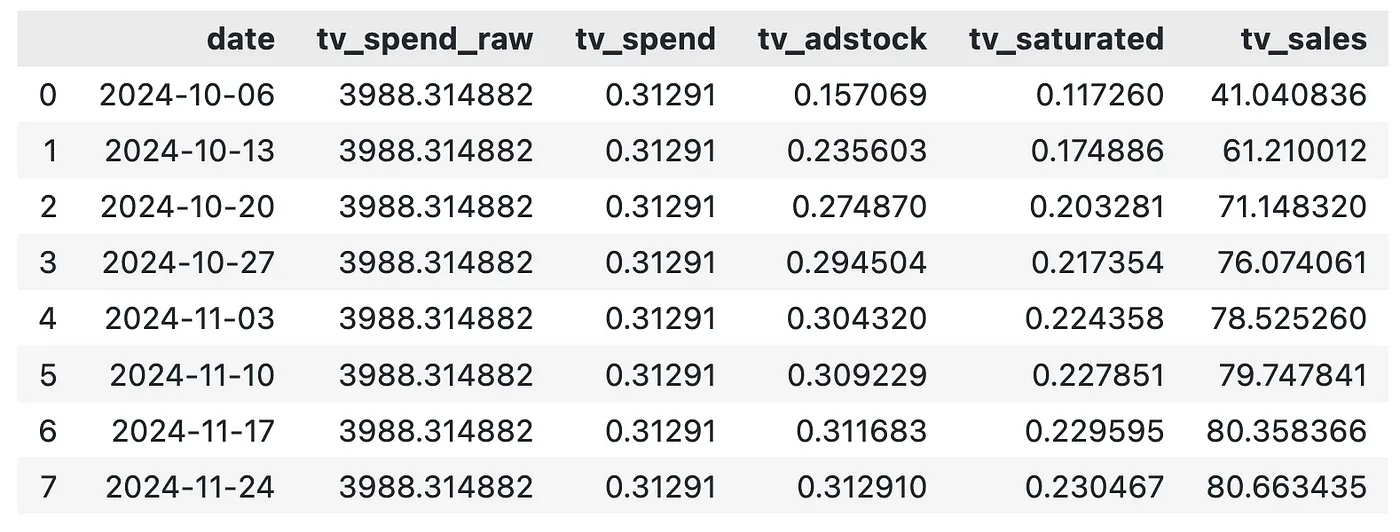
df_exp_tv = exp_generator(start_date, periods, channel, adstock_alpha, saturation_lamda, beta, weekly_spend, max_abs_spend)
# 输出生成的实验数据
df_exp_tv 用户生成的图片
虽然我们每周在电视上的花费相同,但电视的贡献会有所变化。这是由广告效果递延效应导致的,因此,我们最好采用每周贡献的平均值。
周销售额 = df_exp_tv["tv_sales"].mean() # 计算每周的平均销售额
# 这里展示计算后的周销售额结果用户上传的图片
2.3 处理实验数据我们现在有了实验结果,需要对它们进行处理,以便按格式添加到模型中。其中每行代表一个实验的数据框,格式如下所示:
channel:被测试的渠道x:测试前的渠道花费delta_x:对x的调整delta_y:由于delta_x推断出的销售额变化sigma:估计的delta_y的标准差
我们没有通过带有不确定性的度量来模拟实验结果中的不确定性,因此将sigma设定为提升值的5%。
# 包裹了每周销售数据的波动和增量计算的DataFrame定义
df_lift_test = pd.DataFrame({
"channel": ["tv_spend_raw"],
"x": [0],
"delta_x": weekly_spend, # 每周的销售波动
"delta_y": weekly_sales,
"sigma": [weekly_sales * 0.05], # 每周销售的增量
}
)
df_lift_test这张图片是用户上传的
在sigma方面,理想的情况是你能够为你的结果的不确定性获得一个度量,这通常可以通过大多数转化率提升或地域提升测试来实现。
2.4 调整模型我们现在将重新训练那个在第一篇文章中提到的模型。我们将以同样的方式准备训练数据。
- 将数据拆分为特征和目标。为训练数据和非实时数据切片创建索引,这将帮助我们验证模型的效果。
# 设置日期列
date_col = "date"
# 设置结果列
y_col = "sales"
# 设置营销变量
channel_cols = ["tv_spend_raw",
"social_spend_raw",
"search_spend_raw"]
# 设置控制变量
control_cols = ["demand_proxy"]
# 创建数据集
X = df[[date_col] + channel_cols + control_cols]
y = df[y_col]
# 设置外部样本长度
test_len = 8
# 创建训练和测试索引
train_idx = slice(0, len(df) - test_len).start + slice(0, len(df) - test_len).stop
out_of_time_idx = slice(len(df) - test_len, len(df)).start + slice(len(df) - test_len, len(df)).stop接着我们加载从第一篇文章保存的模型,并在添加实验结果之后重新训练该模型:
mmm_default = MMM.load("./mmm_default.nc") # 加载默认的MMM模型
mmm_default.add_lift_test_measurements(df_lift_test) # 添加提升测试测量
mmm_default.fit(X[train_idx], y[train_idx]) # 对模型进行拟合这次我们不讨论模型诊断,但如果你想了解的话,可以看看笔记本。
2.5 验证模型的有效性所以让我们来看看这个新模型和实际效果相比如何。下面我们就来瞧瞧真正的贡献值。
channels = np.array(["tv", "social", "search", "demand"])
true_contributions = pd.DataFrame({'Channels': channels, 'Contributions': contributions})
true_contributions = true_contributions.sort_values(by='Contributions', ascending=False).reset_index(drop=True)
true_contributions = true_contributions.style.bar(subset=['Contributions'], color='lightblue') # 使用浅蓝色
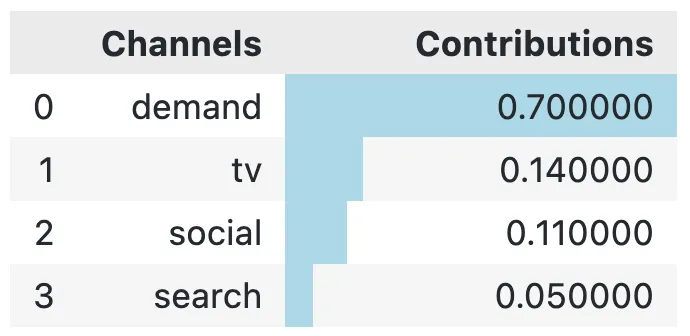
显示 true_contributions用户分享的图片
当我们比较真正对新模型的贡献时,我们看到电视的贡献现在非常接近于其他贡献(相比之下,我们第一篇文章中的模型,电视的贡献仅为24%!)
mmm_default.plot_waterfall_components_decomposition(figsize=(10,6)); # 绘制瀑布图分解图,设置图形大小为10x6英寸用户自己上传的图片
搜索和社交的贡献仍然被高估了,但我们也可以在这里做一些实验来应对这种情况。
最后的感想今天我们向你们展示了如何通过实验结果来引入先验。pymc-marketing 这个包让分析师在运行模型时更加轻松。如果你想深入了解一下它是如何工作的,可以看看他们的教程:
[提升模型校准 - 开源营销分析解决方案你可能听说过“所有模型都是错误的,但有些是有用的”这句话。这在很多地方都适用,而且……mmm_lift_test.html
www.pymc-marketing.io](https://www.pymc-marketing.io/en/stable/notebooks/mmm/mmm_lift_test.html?source=post_page-----49dce1a5b33d--------------------------------)
不过,可别被骗了……在让模型变得准确的道路上,你还是得多面对一些难题……
在物流和资源配置方面的挑战,比如你能在多少地理区域或渠道之间进行资源配置的限制,或者在争取营销团队支持新的实验时遇到困难,仅是其中的一些挑战而已。
值得考虑的一点是完全停止市场营销活动一段时间,利用这段时间的结果来预测需求和基本销售额。这有助于解决物流方面的难题,同时也能增强实验的有效性,因为这样可以增强效果。
希望你享受了这篇第二部分的内容!如果你想继续这条掌握MMM的道路,请关注我!在下一篇文章里,我们将开始思考如何更好地优化营销预算!
共同学习,写下你的评论
评论加载中...
作者其他优质文章