Transformer解码器推理时是自回归的,训练时是非自回归的。
这里的推断是指在进行预测或输出的过程中。
什么是自回归?
在机器学习中,术语“自回归”(autoregressive)来源于时间序列。
在深度学习领域,这类自回归模型通过预测序列中的每个新数据点来生成数据点序列,每个新的数据点都基于之前生成的数据点。
术语 自回归 指的是自回归模型或过程,其中现在的数值是根据之前的历史数值来预测的。
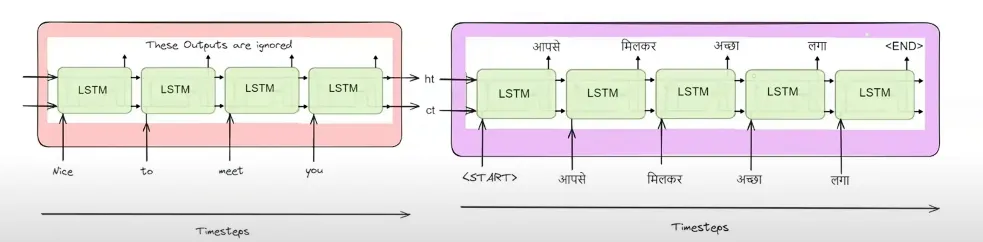
我们之前见过类似的东西。比如编码器-解码器结构。
编码器-解码器架构
在解码器部分中,为了在下一个时间戳生成输出,它会利用前一时间戳的隐藏状态和输出。
在这里,为了在任意时间点生成输出,我们利用了前一个时间点生成的结果。
所有的 seq2seq 模型都是,可以说,自回归的。
这里这些模型一次只生成一个结果。为什么没有模型能一次性生成整个结果?这是因为,在生成任何结果时,模型需要知道之前生成了什么。换句话说,当前的词取决于之前的输出。
因此这些模型是自回归的,无法一次性生成完整输出。另外,这里的数据是序列数据。
这就是原因,因为变换器也是自回归模型的一种
所以我们可以理解为,解码器在解码时是自回归的
现在我们来看看我们为什么说在训练时变压器是非自回归的。这是因为所谓的“masked self 注意”。
在训练过程中,假设变压器是自回归地工作。
这意味着变压器的解码器层逐个产生一个输出单词。
在训练解码器的过程中,我们在编码器-解码器架构中遇到了一个叫作“教师强制”的概念。这意味着即使解码器在前一个时间步的输出是错的,但在下一个时间步,我们会把正确的输出当作输入,而不是直接使用前一个时间步的错误输出。
所以这个输出过程也是具有自回归特性的,因为输出是根据前一个时间戳的值生成的。
但是这里有问题由于训练过程具有自回归的特性,我们的训练过程非常慢。
但我们让训练过程采用自回归的方式,因为我们需要输出序列化的数据,所以自回归是我们的唯一选择,所以我们只能选择自回归。
在训练过程中,我们并不需要依赖于前一个时间戳生成的输出。这是因为这里使用了教师强迫的概念。前一个时间戳的输出正确与否无关紧要,对于当前时间戳,我们总是发送正确值,无论前一个时间戳的输出是否准确。因此,解码器内部的时间戳之间不存在依赖关系,解码器内的这些操作可以并行执行。
同样的情况也发生在变换器内部,它在训练过程中不具有自回归特性。
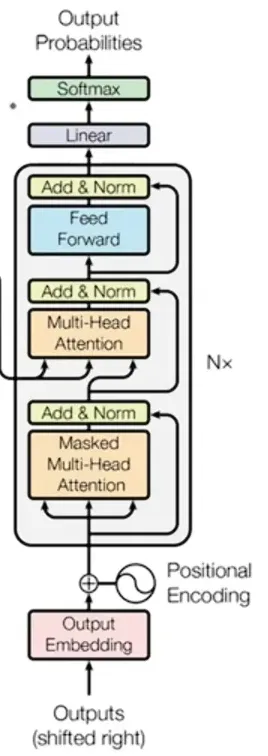
关于并行化的问题变压器中的解码器模块
现在,在解码器区块中,如果我们仔细看,会看到一个名为“Masked Multi Head Attention”的区块。暂时先忽略“masked”这个词,我们知道Multi Head Attention就是多个自注意力区块的组合。为了简单起见,我们将它视为“自注意力”区块。
在自注意力块中,每个词的词嵌入是由该句子中其他词嵌入的混合形成的。
例如,当句子“My name is Abhishek”传到自注意力层时,可以说“我的”这个词的词嵌入是“名字”、“是”和“Abhishek”这几个词嵌入的组合。
在这张图片中,每个来自输入句子“money bank grows”的词在生成自己的词嵌入时都会参考其他词。
所以我们就可以这样写啦。
如图1
从上图可以看出,‘money’的新嵌入向量是通过结合‘money’嵌入向量的70%,‘bank’嵌入向量的20%和‘grows’嵌入向量的10%构建而成的。
这里的每个词的嵌入向量都表示为其他词的嵌入向量的混合或叠加。
但是在这里,当写到“钱”这个词,比如我们刚刚看到的,来创建它的上下文嵌入时,它依赖于“银行”和“增长”这两个基本上就是将来的输入的词
同样,当‘bank’这个词被添加到句子中,以创建其上下文嵌入,正如我们刚刚看到的,它依赖于‘grows’这个词,这个词实际上代表了未来的输入。
我们可以在这个训练过程中使用这种方法,因为数据集是存在的,但在推断阶段会出现问题,因为不知道下一个词会是什么,所以图1中的方程式可能是什么都无法确定,因此这些方程式就无法用了,因为它们包含未来的信息。这就是数据泄露的典型情况。
如果我们当时使用了自回归方法或序列方法进行训练,我们就不会遇到数据泄露的问题。
所以我们使用并行方法时就会面临这种问题。
现在我们有点卡住了 情况1 当我们使用自回归模型时,训练时间变得非常慢,但是没有遇到数据泄露的问题 情况 2: 当我们用并行方法时,训练速度很快,但有个数据泄露的问题。 有没什么好办法能在缩短训练时间的同时,也不会有数据泄漏的问题?那么,这就是掩码多头注意力机制开始发挥作用的地方。
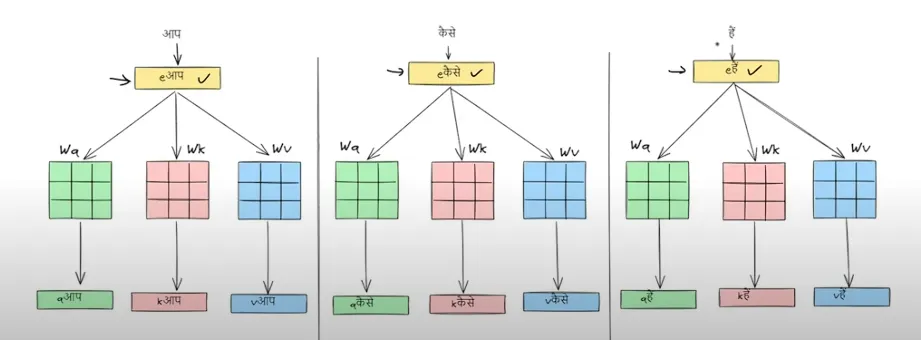
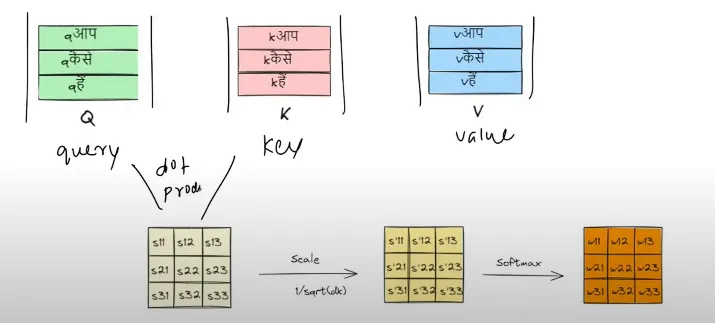
我们来看看这句话“AAP KAISE HAI”在经过自注意力层后会变成什么样。
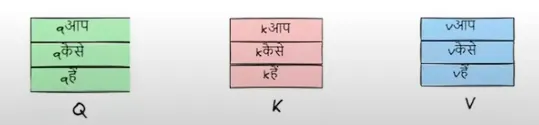
我们现在会把这些查询、键和值的向量都堆叠到矩阵里。
之后,我们对query matrix和key matrix进行点积计算
这就是自注意力机制的全部流程
为了计算“AAP”的上下文嵌入,我们不需要“KAISE”和“HAI”这两个词,因为它们是后续的输入。
同样,我们不需要“HAI”这个词来计算“KAISE”的上下文嵌入,因为“HAI”是后面要用到的词。
所以我们需要在上面的方程里去掉他们的贡献。
这意味着 w12乘以KAISE的向量嵌入,w13乘以HAI的向量嵌入,w23乘以HAI的向量嵌入应该等于零
也就是说,w12、w13 和 w23 都应该是 0
所以,在自注意力部分,当我们通过查询向量和键向量的点积得到矩阵后,我们会接着做以下操作。
我们引入了一个与查询向量和键向量点积形成的矩阵具有相同维度的掩码矩阵,然后正如上所示,我们将掩码矩阵与点积形成的矩阵相加。
在这个掩码矩阵中,我们将某些值设为零,这样它们就不会影响其他值,还将一些值设为负无穷(因为我们希望那些地方的权重为0,而且softmax(-∞) 的结果是 0)。
softmax函数
共同学习,写下你的评论
评论加载中...
作者其他优质文章