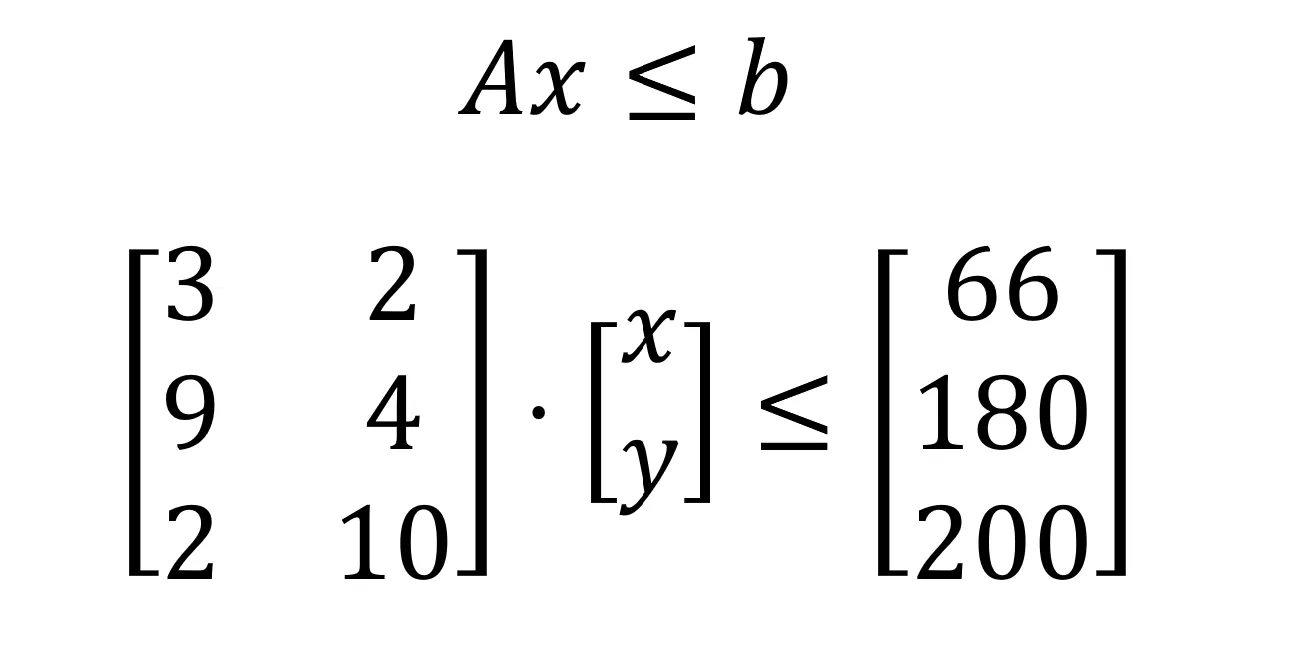线性规划中的优化流程详解：从问题定义到结果提取

在这篇发表于 2021 年的 文章 中，我展示了如何使用 Python 的 Pyomo 包和 Julia 的 JuMP 包来解决线性优化问题。我还介绍了各种可用于解决线性、混合整数或非线性优化问题的商业和开源求解器。

在这篇文章中，我将介绍用于表示优化问题的MPS文件、求解器的求解过程以及解文件的格式。为此，我将使用与前一篇文章中相同的问题，但增加了额外的边界条件。我将使用一个名为HiGHS的开源求解器来进行此操作。HiGHS被誉为是最强大的开源求解器之一，特别擅长解决线性优化问题。在Python中，我只需通过安装highspy 库来获取该求解器，使用pip install highspy即可完成安装。

那咱们就开始吧。

照片由 Unseen Studio 拍摄.

问题说明如下。x 和 y 是两个决策变量。目标是使利润最大化，需满足三个条件的约束。x 和 y 各自有下限和上限。

    利润 = 90x + 75y  
    目标：使利润最大化，在以下条件下：  
    3x+2y小于或等于66  
    9x+4y小于或等于180  
    2x+10y小于或等于200  

    约束如下：  
    其中 2≤x≤8  
    其中 10≤y≤40

在下面的代码里，我将模型命名为 h。然后，我引入了我的决策变量 x 和 y，并分别设定了它们的最小值和最大值，并给它们命名。接着，我添加了三个约束条件，分别标记为 c0、c1 和 c2。每个约束都有 x 和 y 的系数，以及右侧的值。然后，我设法最大化 90x+75y 的值，这就是我们要优化的目标函数。模型在这行中运行。

    import highspy  
    # import numpy as np  # 这行虽然导入了numpy，但代码中并未使用，可以考虑删除或注释掉  

    # 初始化模型  
    h = highspy.Highs()  

    # 定义决策变量  
    x = h.addVariable(lb = 2, ub = 8, name = "x")  
    y = h.addVariable(lb = 10, ub = 40, name = "y")  

    ## 设置求解器为内点法（注释掉了这行代码）  
    # h.setOptionValue("solver", "ipm")  

    # 定义约束条件  
    h.addConstr(3*x + 2*y<=66)  # c0  
    h.addConstr(9*x + 4*y<=180)  # c1  
    h.addConstr(2*x + 10*y<=200)  # c2  

    # 最大化目标函数  
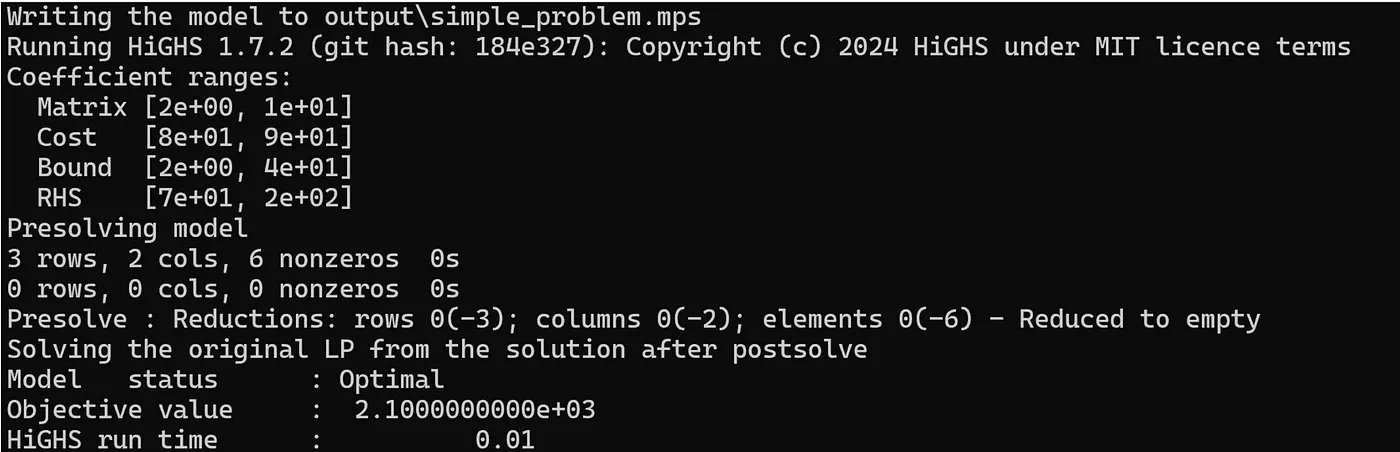
    h.maximize(90*x + 75*y)

当模型在运行时，可以看到以下进度信息。但具体发生了什么？我下面简单说一下。

问题大小:

线性问题中的约束条件可以用矩阵形式Ax≤b来表示，其中A是约束系数矩阵，x是决策变量向量，而b是右侧值的向量。对于这个问题，约束条件以矩阵形式表示如下：

这里以矩阵形式展示了约束，插图由作者绘制。

问题矩阵的大小由行数、列数和非零元素数量来定义。行数指的是约束的数量（这里为3），列数指的是决策变量的数量（这里为2），而非零元素指的是系数，这些系数都不为零。在所有三个约束条件中，都没有系数为零。因此，非零元素的总数为六个。

这是一个非常简单的例子问题。实际上，行数、列数和非零元素的数量可能达到数千乃至数百万。随着问题规模的增大，模型的复杂性也随之增加，从而延长了求解所需的时间。

系数范围
x和y的系数范围在问题中是2到10。所以矩阵系数的范围表示为[2e+00, 1e+01]。

成本在这里是指目标函数。x的系数是90，y的系数是75。因此，成本的系数范围是[80, 90]。

x 和 y 的取值都在 2 到 40 之间。因此，Bound 的系数范围在 [2e+00, 4e+01] 之间。

系数介于66和200之间。因此，右侧的系数范围为[66, 200]。

预求解
预求解 是求解器尝试求解优化问题时的初始过程，它首先试图简化模型。例如，它会将超出特定阈值的系数视为无穷大。预求解的目的是创建一个简化版的问题矩阵，该矩阵的目标函数与原问题相同，并且其可行域可以映射到原问题的可行域。

在这种情况下，预求解步骤仅用了两次迭代就完成了，结果得到了一个空矩阵。这也表明解决方案已经找到，不需要进一步优化。它返回的目标值是2100，HiGHS求解器的运行时间仅为0.01秒。获取解决方案后，求解器可以进行后处理或反预处理步骤，将解决方案映射到原始问题的可行区域。

MPS格式是一种用于表示线性及混合整数线性规划问题的文件格式。尽管MPS是一种相对古老的格式，但它被所有商业线性规划求解器支持。线性问题还可以用其他格式如LP、AMPL和GAMS来表示。

可以使用 highspy 通过简单的 h.writeModel("foo.mps") 来写入 mps 文件。读取 mps 文件也同样容易，只需 h.readModel("foo.mps")。

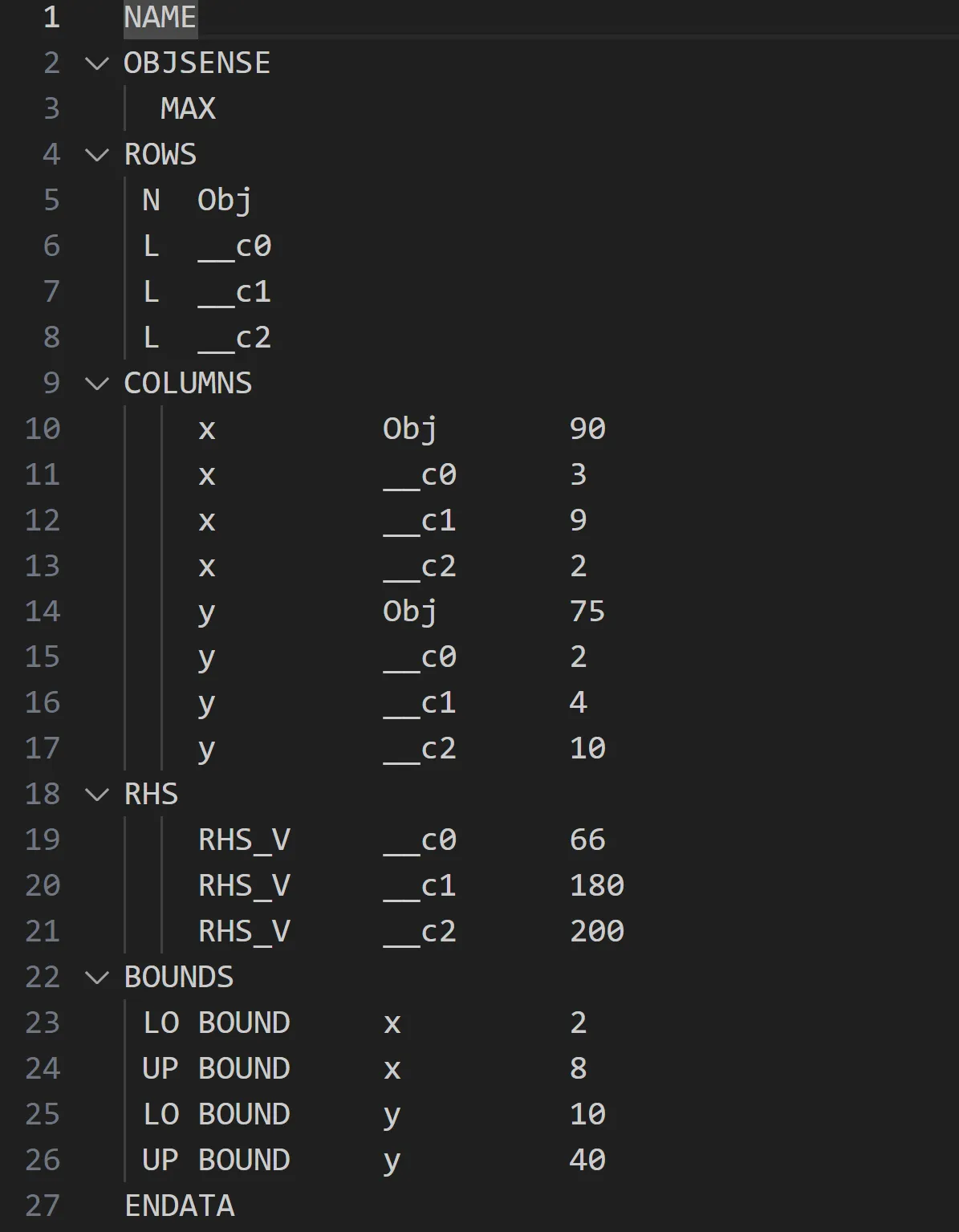
给定LP问题的MPS格式。作者提供。

下面展示了给定优化问题的MPS文件结构。它以LP问题的名称NAME开始。OBJSENSE指示问题是否为最小化（MIN）或最大化（MAX），这里指的是最大化（MAX）。ROWS部分表示目标行、所有约束的名称及其类型，即等式/不等式。E表示等式，G表示大于等于行，L表示小于等于行，N表示无限制行，这些是约束的类型。具体来说，三个约束条件分别为c0、c1和__c2，其中Obj是目标行的简称。

在COLUMNS部分中，决策变量的名称（这里比如是x和y）在左边指定，它们的系数（属于目标函数或约束条件）则在右边列出。RHS部分包含模型约束的右侧项。决策变量的下界和上界在BOUNDS部分定义为。MPS文件以ENDATA结束标志。

HiGHS 使用诸如单纯形法或内点法之类的算法来进行优化。解释这些算法本身可以写一篇独立的文章。希望将来详细探讨它们。

以下给出了用于提取结果的代码。模型的状态是最优的。我提取了目标函数值以及决策变量的解。此外，我还打印了迭代次数、原始问题和对偶问题解的状态，以及基的合理性。

    solution = h.getSolution()  
    basis = h.getBasis()  
    info = h.getInfo()  

    model_status = h.getModelStatus()  
    print("模型状态为：", h.modelStatusToString(model_status))  
    print()  

    # 获取目标函数的最优值，x和y的最优解  
    print("最优目标函数值为：", info.objective_function_value)  
    print("x的最优解为：", solution.col_value[0])  
    print("y的最优解为：", solution.col_value[1])  

    # 获取模型运行特性  
    print('迭代次数为：', info.simplex_iteration_count)  
    print('原始解状态为：', h.solutionStatusToString(info.primal_solution_status))  
    print('对偶解状态为：', h.solutionStatusToString(info.dual_solution_status))  
    print('基的解的有效性为：', h.basisValidityToString(info.basis_validity))

下面打印的是上面代码的结果，插图由作者绘制。

优化完成后，HiGHS 允许将解决方案写入带有 .sol 扩展名的解决方案文件中。此外，解决方案可以以不同的格式输出，具体格式请参考 这里。其中，1 表示 HiGHS 的漂亮格式，3 表示 Glpsol 的漂亮格式。

可用的解决方案文件样式，HiGHS提供的。参考HiGHS文档如下。

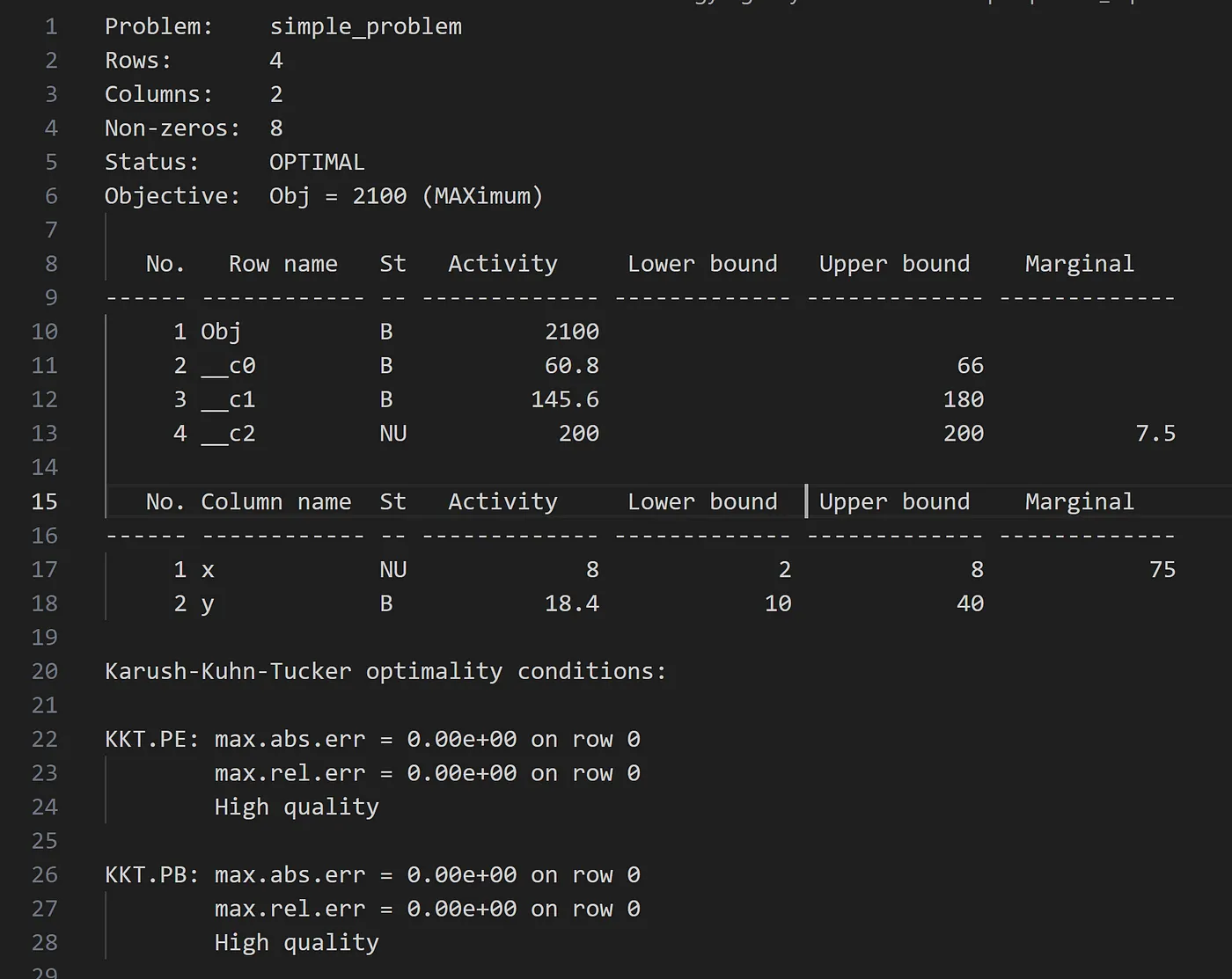
为了获取风格3的解决方案，我使用了h.writeSolution("mysolution.sol", 3)。统计信息位于顶部提供。最优解值则显示在Activity列中。St列则指了解的状态。例如，B表示该变量或约束属于基础解（最优状态）的一部分。NU表示该解是非基本的，并且与上限相等。Marginal列中的值（通常称为影子价格或对偶值）指的是目标函数对非基本变量单位变化的反应。有关GLPK解决方案文件信息的更多详情，可参考这里。

Glpsol解决方案文件的结构（简洁样式）。插图由作者提供。

在这篇文章中，我展示了如何使用Python中的highspy包和一个名为HiGHS的开源求解器解决一个简单的线性优化问题。接着，我解释了如何通过系数矩阵、决策变量向量和右侧常数向量来确定优化问题的大小。我还介绍了用来表示优化问题的数学编程系统（mps）文件的各个部分，并解释了这些部分的含义。最后，我演示了求解器的优化过程，如何提取结果以及如何分析解决方案文件。

这个帖子的相关笔记本和文件可以在GitHub上的这个repository找到。谢谢大家！