当平均值骗人：超越单一预测点

有些人喜欢热咖啡，有些人喜欢冰咖啡，但没有人喜欢温咖啡。然而，一个仅基于咖啡温度训练的简单基于温度的模型可能会预测下一杯咖啡将是温的。这说明了预测建模中的一个基本问题：专注于单一的点估计（例如平均值）可能导致我们得出毫无意义甚至误导性的结论。

在《水晶球谬误（Merckel，2024b）》中，我们探讨了即使一个完美的预测模型也无法确切告诉我们会发生什么——它只能告诉我们可能发生的情况及其可能性。换句话说，它揭示出随机变量的真正可能分布。尽管这样的完美模型依然是理论上的，但在实际应用中的模型也应尽可能接近这些真实分布。

然而，许多企业在使用的预测模型却做着截然不同的事情：他们仅关注点估计，通常是均值或众数，而不是试图捕捉所有可能的情况。这不仅仅是使用预测方式的问题；这种局限性在很多传统机器学习算法的设计中是固有的。随机森林、广义线性模型(GLM)、人工神经网络(ANN)、梯度提升机等，在回归任务中，它们被设计成预测分布的期望值（即均值）。在分类问题中，虽然逻辑回归和其它GLM模型会自然地估计类别的概率，但像随机森林和梯度提升这样的树基方法会生成需要额外校准步骤（如同序回归或Platt校准）才能转化为有意义概率的原始得分。但在实践中，这种校准很少被执行，即使不确定性信息（即概率值）可用，也通常会被丢弃，而仅保留最有可能的类别（即众数）。

这种简化有时不仅不足以描述问题，还会导致根本错误的结论，就像我们用于预测冷热不均的咖啡的模型一样。一个鲜明的例子是，在2008年金融危机之前用于定价资产担保债务凭证（CDOs）的高斯相关函数。通过将复杂的抵押贷款违约关系简化为单一的相关数字，以及其他问题，该模型严重低估了同时违约的可能性（MacKenzie & Spears, 2014）。这种对极端风险的系统性低估如此普遍，以至于像 Nassim Taleb 建议的 Universa Investments 这样的一些投资基金，已经采取策略利用这种低估。他们认识到市场一贯低估极端事件的概率及其影响（Patterson, 2023）。当我们把可能结果的复杂分布简化为单一数字时，我们便会失去关于不确定性、风险和可能对决策产生重大影响的极端事件及其潜在影响的关键信息。

另一方面，一些量化交易公司通过正确地建模这些复杂的分布，部分地取得了成功。当被问及Renaissance Technologies的方法时——其Medallion基金据说在1988年至2018年间（扣除费用前）每年收益达到了66%（Zuckerman, 2019）——Jim Simons强调，他们仔细考虑市场风险“通常不是正态分布，分布尾部较重，内部却较轻”（Simons, 2013, 47:41），突显了超越简单平均数观察的重要性。

为什么我们仍然坚持使用点估计，尽管它们存在明显的局限性？原因可能既有实际的，也有文化的。从技术角度看，预测分布比预测单个数值更具挑战性，需要更复杂的模型和更多的计算资源。更根本的是，大多数商业流程和工具并未被设计成能够处理分布思维的方式。你无法在一个电子表格的单元格里输入一个概率分布，而且许多决策框架倾向于具体数字而不是可能性的范围。此外，正如 Kahneman (2011) 所提到，他在分析人类决策时指出，我们天生更倾向于思考具体的场景而非统计分布——我们的直觉思维更偏爱简单具体的答案，而不是概率性的答案。

我们可以通过实际的房地产市场数据来说明单一估值点的局限性，以及捕捉可能值完整分布的建模方法，以展示潜在问题和模型技术。

在这个部分，我们使用法国政府（gouv.fr，2024年）提供的法国房地产交易（DVF）数据集，该数据集包含法国各地房产交易的详细记录。我们这次分析关注2014年至2024年间房产的售价、房屋面积和房间数。需要特别指出的是，我们排除了地理位置等关键信息，因为我们的目标并非预测房价，而是展示预测分布的好处，不仅仅是依赖单一的点估计。

首先，我们将通过一个虚构的、但可能是基于真实事件的案例研究，展示一种常见的机器学习技术是如何被用于规划一项雄心勃勃的房地产项目的。然后，我们会批判性地审视这个案例，并提出一些大家可能更喜欢的替代方案，以便更好地准备这项交易。

荷马和丽莎住在巴黎。他们预计家庭成员会增多，计划卖掉他们的两居室公寓，用来购买一套四居室的房产。考虑到运营和维护成本，以及他们新买的带有所有选项的高端Roomba扫地机器人的功能，他们认为90平方米的面积刚刚好。他们想估算一下需要节省或借款多少来补充卖房所得。荷马在去年研究生毕业前修了一门关于机器学习的在线课程，毕业后立即通过社交网络找到了在一家大型传统公司里的数据科学家职位，这家公司正在大力投资（从零开始）扩展其人工智能能力，以避免错失机会。现在已经是该公司的高级首席数据科学家，经过近一年的工作经验，他已经掌握了相当多的知识！（他甚至在一家动物园也有兼职工作，他在那里表现优异——梅克尔，2024a。）

经过一番谷歌搜索，他找到了政府免费提供的房地产数据集。他做了一些清洗、过滤和聚合，从而获得了用于他普通最小二乘模型（OLS，对于内行来说）的完美数据。现在他可以自信地预测巴黎地区的房价，既可以依据房间数量，也可以依据面积。他们的两室40平方米的公寓价值365,116欧元。而一个四室90平方米的则达到804,911欧元。这显而易见，他们必须计算出差价，即439,795欧元。

荷马和丽丝真的需要存439,795欧元或借这笔钱吗？模型确实这样建议。但这真的是这样吗？

如果荷马知道的话，也许他能给出置信区间吧？使用 OLS（普通最小二乘法），置信区间可以利用自助法进行经验估计，或者通过基于标准误差的分析方法进行计算。

不仅如此，甚至在那之前，他本可以看看价格分布，从而发现默认的OLS方法可能不是最佳选择。

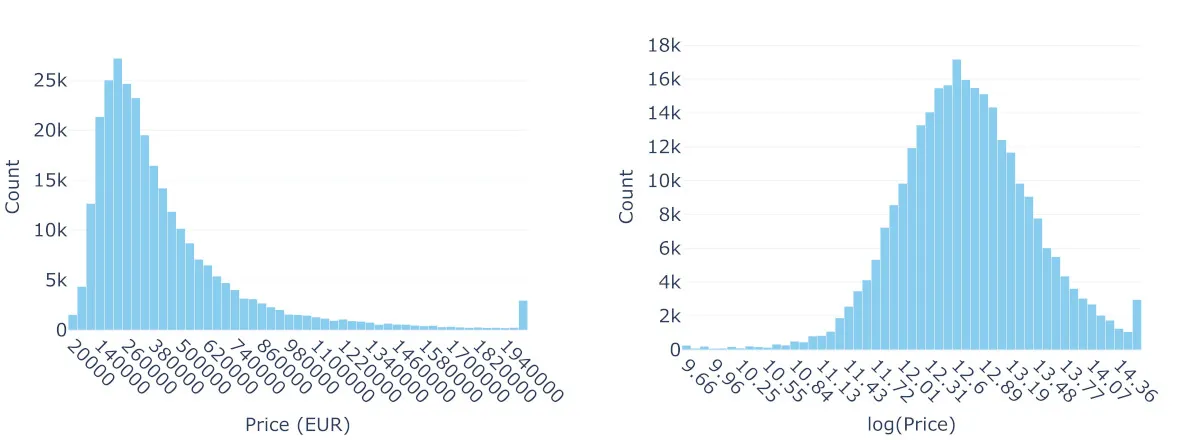
图1：巴黎附近房地产价格（2014–2024）： 左图展示了巴黎市中心7公里范围内房地产价格的分布。右图则展示了这些价格的自然对数分布。两个直方图中的最后一格代表了价格超过2,000,000€（或对数尺度下的log(2,000,000)）的房产数量。图片由笔者提供。

右偏的形状，带有长长的尾部，很难不被注意到。对于预测建模（而不是解释性建模），主要关注点不是OLS的误差正态性（和同方差性），而在于长尾中的极端值可能对模型造成不成比例的影响——OLS通过最小化平方误差来工作，这使得它对极端观测值尤为敏感，尤其是那些与误差假设的正态分布有显著差异的观测值。

广义线性模型（GLM）通过直接为响应变量指定一个来自指数族的分布，并使用“连接函数”将线性预测器与该分布的均值连接起来，扩展了线性模型的框架。虽然线性模型假设误差正态分布并通过线性预测器直接估计响应的期望E(Y)，但GLM允许使用不同类型的响应分布，并通过使用连接函数，将线性预测器与E(Y)的期望值相连接。

让我们再次看看荷马和丽萨的情况。我们不必实现广义线性模型（GLM），而是可以通过对价格取自然对数来转换数据，然后再应用线性模型。这意味着我们在假设价格遵循对数正态分布（图1展示了价格分布及其对数版本如下所示）。在将预测转换回原始尺度时，我们需要使用杜安的涂抹估计量（Duan, 1983）来校正对数转换引入的偏差。使用这种偏差校正的对数正态模型，并将其拟合到巴黎周边的房产，他们目前的两居室40平方米公寓估计价值为337,844欧元，而他们目标的四居室90平方米房产则估计需要大约751,884欧元，因此，他们还需要额外的414,040欧元。

带有抹平校正的对数正态模型特别适合这种情境，因为它不仅反映了乘法关系，例如当房间数量或面积增加时，价格会按比例增加（乘以一个因子），而不是按固定数额增加，而且还能恰当处理重新转换偏差问题，否则这种偏差会导致价格系统性低估问题。

为了更好地理解这些预测中的不确定性，可以考察这些置信区间。95%自助法置信区间估计的均值价格差[400,740€ — 418,618€]意味着如果我们重复这个抽样过程多次，约95%的这种区间会包含真实的均值价格差。这个区间在这种情况下比基于标准误差的95%置信区间更可靠，因为它不受模型对误差分布或模型规范严格性的假设限制。相反，它捕捉了观察数据的变异性与复杂性，考虑了未建模的因素以及可能偏离理想假设的因素。例如，我们的模型仅考虑了房间数量和面积，而巴黎的房地产价格受多种因素的影响——距地铁站的距离、建筑风格、楼层、建筑状况、当地社区动态，甚至更广泛的经济背景，如当前的利率水平。

根据这一分析，对数正态模型为价格差异提供了一个新的且更现实的估计值，即414,040欧元。然而，置信区间虽然在统计上严谨性高，可能不完全符合霍默和丽莎实际规划的需求。相反，为了更好地理解可能的价格范围，并为他们的规划提供更实用的见解，我们可以转向贝叶斯建模，这种方法不仅可以估计潜在价格差异的完整概率分布，而且还可以提供更实用的点估计和置信区间之外的信息。

贝叶斯建模提供了一种更全面的方式来理解预测中的不确定性。它不仅仅计算单一的最佳猜测价格差，或像传统方法那样计算置信区间，而是提供所有可能价格的完整概率分布。

这个过程始于表达我们对房价的“先验信念”——我们基于现有知识对房价的合理预期。实际上，这涉及到为模型参数（例如，房间数量和建筑面积的权重）定义先验分布，并通过似然函数定义数据生成的方式。然后我们将实际的销售数据（我们的“证据”）纳入模型。通过结合贝叶斯定理，我们得出“后验分布”，这提供了参数和预测的更新视图，反映了数据情况下的估计不确定性。这个后验分布正是荷马和丽莎真正感兴趣的。

鉴于价格数据的右偏的特性，对数正态分布似乎是一个合理的假设。这一选择需要通过后验预测检查来验证，确保它能充分捕捉数据的特点。对于参数，可以使用被限制为正的截断高斯分布来反映我们对价格随着房间数量和面积的增加而上涨的假设。这些先验的宽度反映了可能影响的范围，这反映了我们对额外房间或面积如何影响价格的不确定程度。

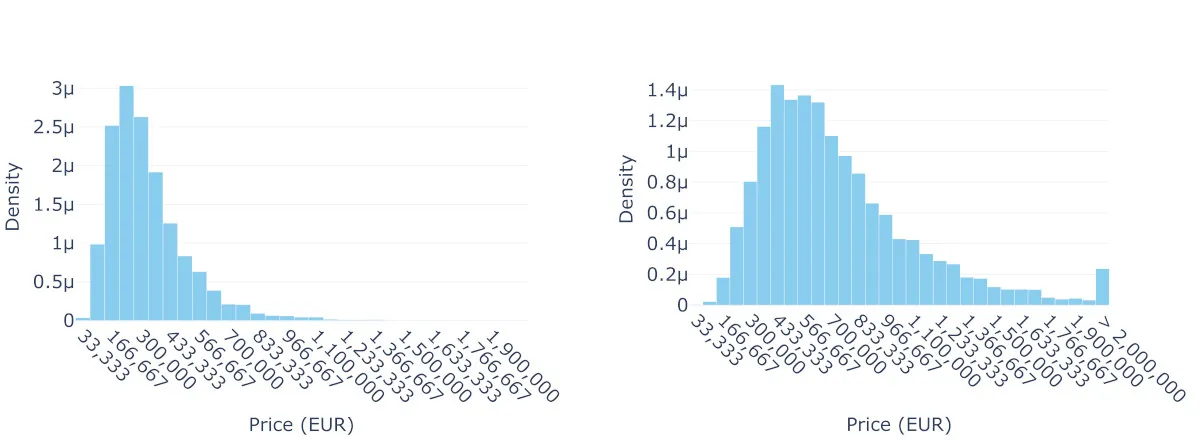
图2：40平方米二房和90平方米四房住宅的预测价格分布： 左图显示了一个40平方米二房住宅的预测价格分布，右图则显示了一个90平方米四房住宅的预测价格分布。图片由作者创作。

贝叶斯方法与我们之前使用的方法形成了鲜明对比。与仅给出单个预测及一些不确定性的范围的普通最小二乘法（OLS法）和所谓的伪广义线性模型（由于对数正态分布不属于指数族）不同，贝叶斯模型提供了每个属性的完整概率分布。图2展示了这些预测的价格分布，不仅给出了点估计，还展示了每种属性类型的可能价格范围。两个分布的重叠区域表明，房屋价格并不完全由大小和房间数量决定——未考虑的因素，如地点质量、建筑状况或市场时机，有时会使较小的房产比大的房产更贵。

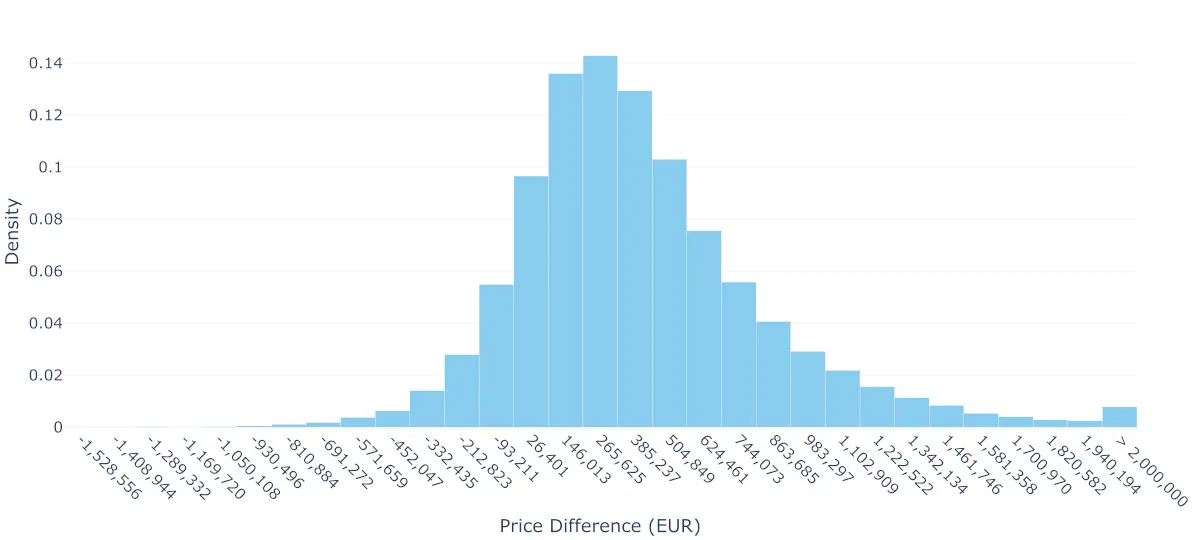
图3：2室（40平方米）和4室（90平方米）房产预测价格差异分布： 这张图展示了通过蒙特卡洛模拟得到的预测价格差异分布，体现了模型参数的不确定性。平均价格差异约为405,697欧元，而中位数为337,281欧元，说明了分布的轻微右偏。关键分位数显示了很大的变化范围：10%分位数为-53,318欧元，25%分位数为126,602欧元，75%分位数为611,492欧元，90%分位数为956,934欧元。448,854欧元的标准偏差突显了这些预测中的显著不确定性。图片由作者制作。

要理解这对霍默和丽萨夫妻的情况意味着什么，我们需要估计这两个房产之间的价格差异分布。通过蒙特卡洛模拟，我们反复从两个预测分布中抽样，并计算它们的差值，生成了如图3所示的分布。结果令人清醒：虽然平均差异表明他们可能需要额外筹集约405,697欧元，但这一数字存在很大的不确定性。事实上，大约13.4%的模拟场景中价格差异为负，这意味着在某些情况下，他们实际上可以从交易中获利。然而，他们也应做好可能需要更多资金的准备——有25%的可能性他们可能需要超过611,492欧元，还有10%的可能性需要超过956,934欧元——以完成升级。

这种更全面的不确定性视图为荷马和丽丝的做决定提供了更好的基础，比我们之前分析中提供的看似精确的单一数字更佳。

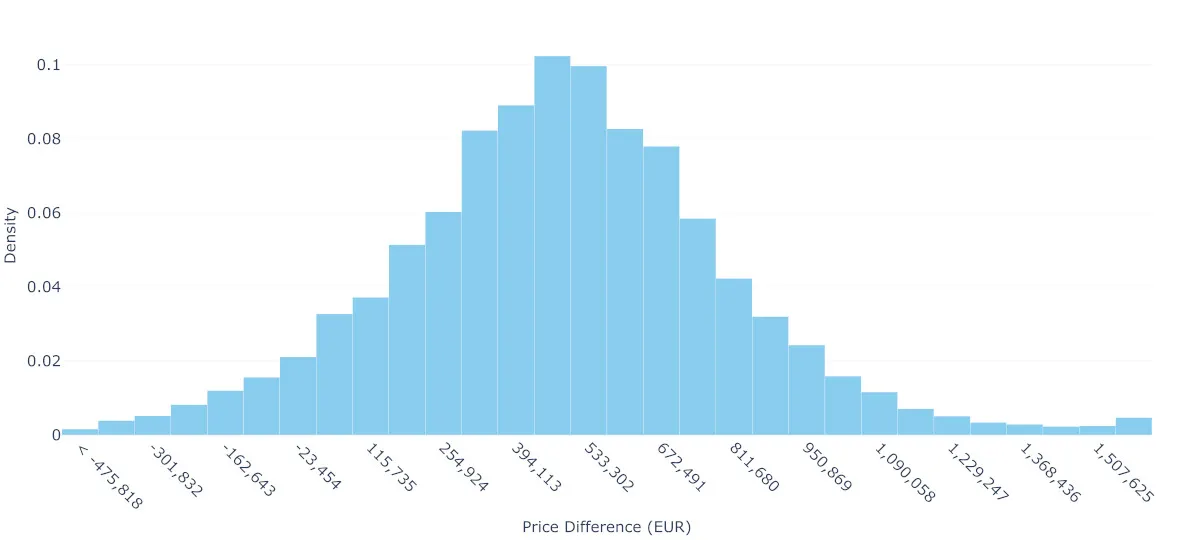
图4：2室（40平方米）和4室（90平方米）房产模拟价格差异分布： 通过蒙特卡洛模拟，随机配对实际交易的2室（35至45平方米）和4室（85至95平方米）房产，得到该分布。平均价格差为484,672欧元（中位数：480,000欧元），90%分位区间从-52,810欧元到1,014,325欧元，显示出较大的波动。位于零以下的阴影部分，大约占6.6%的情景，表示在某些情况下4室房产的价格可能低于2室房产。分布的右偏表明，虽然大多数价格差异集中在中位数附近，但还是存在一些较大的差异。在某些情况下，可能会出现更大差异，其中有5%的情况价格差异超过了1,014,325欧元。图片由作者提供。

与其依赖复杂的贝叶斯模型进行预测，我们可以通过直接分析类似的交易获得清晰的洞察。在巴黎及其周边地区，我们发现了36,265间两居室（35–45平方米）和4,145间四居室（85–95平方米），形成了一套丰富的实际市场行为数据集。

数据显示价格存在显著差异。两居室的平均价格为329,080欧元，中位价格为323,000欧元，90%的价格介于150,000欧元至523,650欧元之间。四居室的价格差异更大，平均价格为812,015欧元，中位价格为802,090欧元，90%的价格范围在315,200欧元至1,309,227欧元之间。

通过蒙特卡洛模拟随机配对房产，我们可以估算荷马和丽莎可能会遇到的情况。平均差价为484,672欧元，中位差价为480,000欧元，50%的情况所需差额在287,488欧元到673,000欧元之间。此外，在6.6%的情况下，他们甚至可能找到一个比他们卖出的两居室便宜的四居室，甚至有机会赚到钱。

这种直接的方法使用实际交易而不是模型预测，不假设价格之间的关系，而是捕捉真实的市场变动。对于霍默和丽萨的规划来说，信息很明确：虽然他们应该准备好大约需要48万欧元，同时也应准备好需要更多或更少的情况。理解这种可能性的范围对他们的财务规划来说很重要。

这个简单的技术在这里特别有效，因为我们有一个包含超过40,000个相关交易的密集数据集，这些交易涵盖了我们的目标物业种类。然而，在许多依赖预测建模的情况下，我们可能会遇到数据稀疏的情况。在这种情况下，我们需要在不同的数据点之间插值，或者超出我们现有的数据外插。这时，贝叶斯模型特别有用……

通过这些分析方法——OLS、对数正态建模、贝叶斯分析和蒙特卡洛模拟——的旅程，不仅提供了价格预测的范围，还强调了我们如何用越来越复杂的方法来处理预测模型中的不确定性。从看似精确的OLS估计（439,795欧元）到对数正态模型的细微之处（414,040欧元），再到贝叶斯和蒙特卡洛方法提供的分布信息（均值分别为405,697欧元和484,672欧元），每种方法都提供了对同一问题的不同视角。

这种进展说明了何时分布性思维开始变得有用。对于像荷马和丽莎面临的那种高风险、一次性决策，理解所有可能的范围能提供明显的优点。相比之下，重复性低风险决策，如在线广告投放，通常可以依赖简单的点估计方法。然而，在尾部风险有重大影响的领域——例如投资组合管理或重大财务规划——建模整个分布不仅有利，而且是根本上明智的做法。

承认这个案例研究中简化了的真实世界复杂性这一点很重要。因素如利率、时间变化、交易成本等显著影响房地产价格。我们的目标并不是要开发一个全面的房价预测器，而是逐步展示从简单的单点估计到完整分布的转变过程。

值得注意的是，鉴于我们主要的目标是展示这一从点估计到分布思维的进展，我们特意保持了模型的简单性。在使用 OLS 和伪 GLM 实现时，没有引入交互项，因此也没有进行正则化或超参数优化，并且仅进行了最小的预处理。虽然房间数量和面积之间的高相关性一般不会对预测建模造成太大问题，但它会影响贝叶斯模型中使用的马尔可夫链蒙特卡罗（MCMC）方法的采样效率，具体表现为后验分布中的峭脊更难以高效探索（确实，我们观察到这些参数之间存在 -0.74 的相关系数，形成了明显的峭脊结构，尽管有效样本量保持在总样本量的大约 50%，表明我们的推断对于说明目的来说足够稳定）。对于贝叶斯方法而言，通过定义更丰富的先验信息或增加额外协变量，有很大的改进空间。虽然这些优化可能会带来一些数值结果的差异，但它们不太可能从根本上改变关于考虑完整分布而非仅点估计的重要性这一关键见解。

最后，我们必须接受，我们对不确定性的理解也是不确定的。我们对分布预测的置信度依赖于模型假设和数据质量。这种“不确定性中的不确定性”不仅挑战我们改进模型，还要求我们透明地传达它们的局限。

接受分布思维不仅仅是一次技术升级——更是一种思维转变。单一预测点可能感觉上是可行的，但它们往往提供一种虚假的精确感，忽略了结果的内在变化性。通过考虑所有可能的结果，我们能够更好地做出明智的决策，并制定出更好的策略来应对现实世界中的随机性。

- 段, N. (1983). 涂抹估计：一种非参数再变换方法. 美国统计学会期刊, 78(383), 605–610. 可从 https://www.jstor.org/stable/2288126 获取。
- 卡内曼, D. (2011). 思考, 快与慢. 电子书版本. ASIN B00555X8OA.
- 麦肯齐, D., & 斯皮尔斯, T. (2014). “杀死华尔街的公式”：高斯联合分布模型及其在投资银行中的应用. 社会学研究, 44(3), 393–417. 可从 https://www.jstor.org/stable/43284238 获取。
- 帕特森, S. (2023). 混沌之王：华尔街交易员如何在危机时代赚取数十亿美元. 电子书版本. ASIN B0BSB49L11.
- 祖克曼, G. (2019). 市场解密者：吉姆·西蒙斯如何开启量化革命. 电子书版本. ASIN B07NLFC63Y.

- gouv.fr (2024). 地价申请（DVF），从https://www.data.gouv.fr/fr/datasets/5c4ae55a634f4117716d5656/ 获取。
- Merckel, L. (2024a). 数据驱动还是被数据误导？来自Hello-World分类器的经验教训。从https://619.io/blog/2024/11/28/data-driven-or-data-derailed/ 获取。
- Merckel, L. (2024b). 水晶球谬误：完美预测模型的真正含义。从https://619.io/blog/2024/12/03/the-crystal-ball-fallacy/ 获取。
- Simons, J. H. (2013). 数学、常识与好运：我的生活与职业。视频讲座。观看地址：https://www.youtube.com/watch?v=SVdTF4_QrTM。

艺术和文字由 Loic Merckel 创作提供。根据 CC BY 4.0 许可协议发布。最初发布在 619.io。如需讨论或互动，可以查看 LinkedIn 版本 或 Medium 版本。否则，请在分享或使用时注明 原始来源。