本文已收录在Github,关注我,紧跟本系列专栏文章,咱们下篇再续!
作者简介:魔都架构师,多家大厂后端一线研发经验,在分布式系统设计、数据平台架构和AI应用开发等领域都有丰富实践经验。
各大技术社区头部专家博主。具有丰富的引领团队经验,深厚业务架构和解决方案的积累。
负责:
- 中央/分销预订系统性能优化
- 活动&券等营销中台建设
- 交易平台及数据中台等架构和开发设计
- 车联网核心平台-物联网连接平台、大数据平台架构设计及优化
- LLM Agent应用开发
- 区块链应用开发
- 大数据开发挖掘经验
- 推荐系统项目
目前主攻市级软件项目设计、构建服务全社会的应用系统。
参考:
0 前言
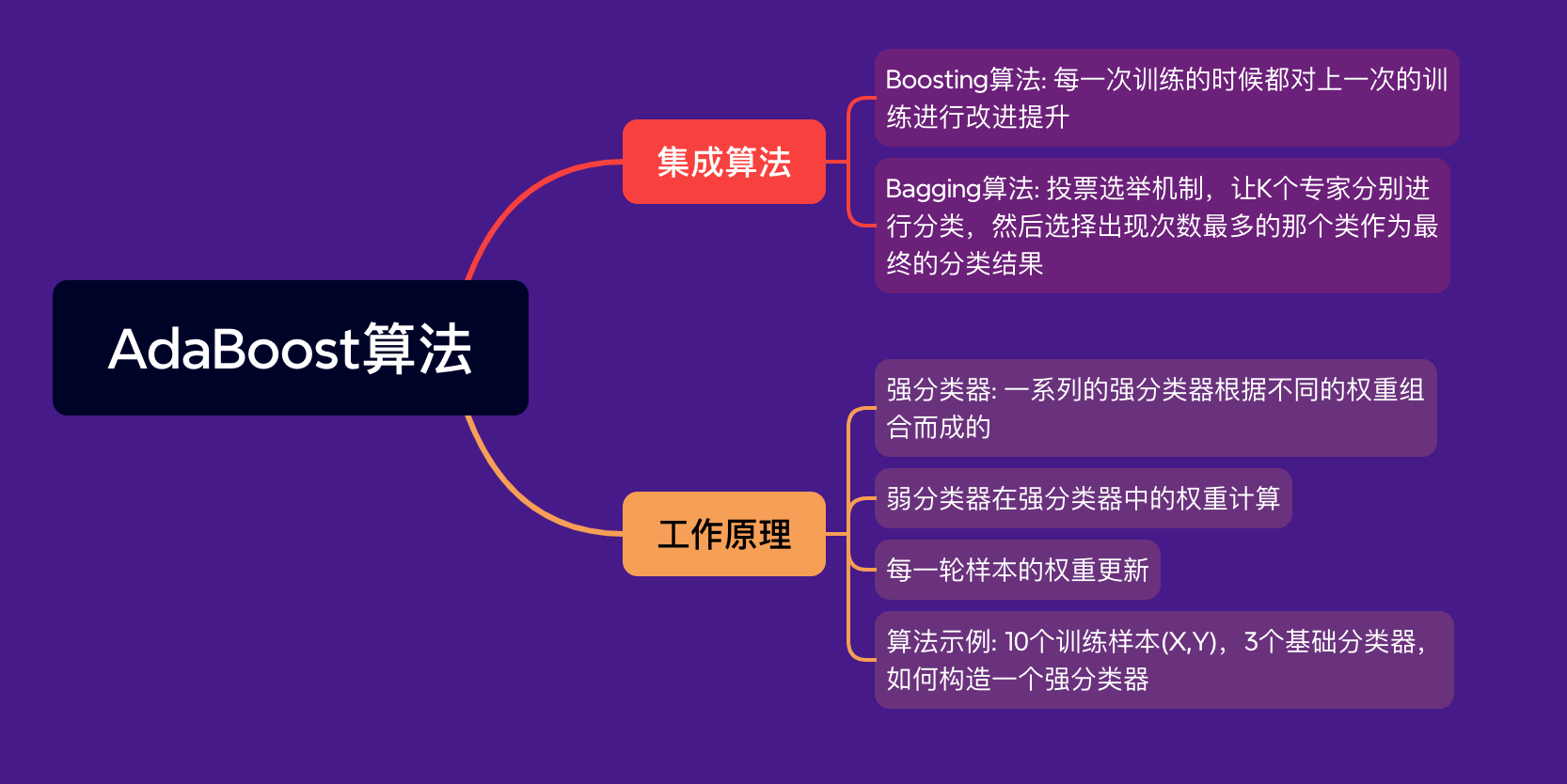
数据挖掘中,分类算法可以说是核心算法,其中AdaBoost算法与随机森林算法一样都属于分类算法中的集成算法。
集成的含义是集思广益,博取众长。决定时,先听取多个专家的意见,再决定。集成算法通常有两种方式:
- 投票选举(bagging):投票选举的场景类似把专家召集到一个会议桌前,当做一个决定的时候,让K个专家(K个模型)分别进行分类,然后选择出现次数最多的那个类作为最终的分类结果
- 再学习(boosting):相当于把K个专家(K个分类器)进行加权融合,形成一个新的超级专家(强分类器),让这个超级专家做判断
Boosting含义是提升,作用是每次训练时,都对上次训练进行改进提升,训练过程中这K个“专家”之间是有依赖性,当引入第K个“专家”(第K个分类器),实际是对前K-1个专家的优化。而bagging在做投票选举的时候可以并行计算,也就是K个“专家”在做判断的时候是相互独立的,不存在依赖性。
1 AdaBoost工作原理
AdaBoost,Adaptive Boosting,自适应提升算法。Freund等人于1995年提出,对Boosting算法的实现。
啥是Boosting算法?
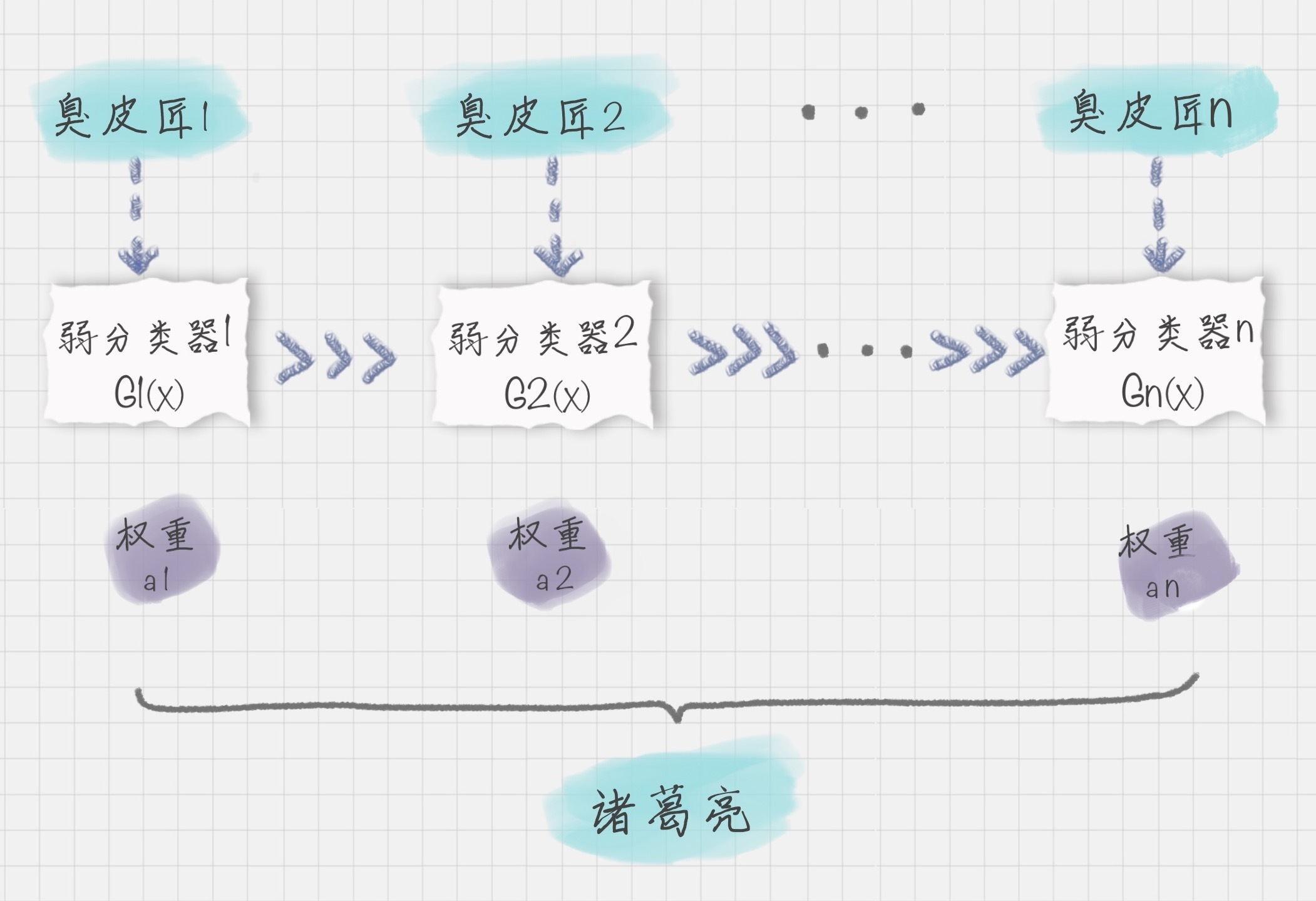
集成算法的一种,也是一类算法的总称。这类算法通过训练多个弱分类器,将它们组合成一个强分类器,也就是我们俗话说的“三个臭皮匠,顶个诸葛亮”。为什么要这么做呢?因为臭皮匠好训练,诸葛亮却不好求。因此要打造一个诸葛亮,最好的方式就是训练多个臭皮匠,然后让这些臭皮匠组合起来,这样往往可以得到很好的效果。
可用上图表示最终得到的强分类器,它通过一系列弱分类器根据不同权重组合而成。
若弱分类器为:
Gi(x)
G_{i}(x)
Gi(x)
它在强分类器中的权重:
αi
α_{i}
αi
可得强分类器f(x):
f(x)=∑i=1nαiGi(x)
f(x) = \sum_{i=1}^{n} \alpha_i G_i(x)
f(x)=i=1∑nαiGi(x)
有这公式,为求解强分类器,会关注:
-
咋得到弱分类器,即每次迭代训练过程,咋得最优弱分类器?
-
每个弱分类器在强分类器中的权重咋计算?
先看第二个问题。K个弱分类器中组成的强分类器中,若:
- 弱分类器的分类效果好,权重应较大
- 弱分类器的分类效果一般,权重应降低
所以要基于这个弱分类器对样本的分类错误率来决定它的权重,公式:
αi=12log1−eiei
α_i = \frac{1}{2} log{\frac{1-e_i}{e_i}}
αi=21logei1−ei
ei e_{i} ei
代表第i个分类器的分类错误率。
再看第一个问题,AdaBoost算法是通过改变样本的数据分布来实现的。AdaBoost会判断每次训练的样本是否正确分类,对于正确分类的样本,降低它的权重,对于被错误分类的样本,增加它的权重。再基于上一次得到的分类准确率,来确定这次训练样本中每个样本的权重。然后将修改过权重的新数据集传递给下一层的分类器进行训练。这样做的好处就是,通过每一轮训练样本的动态权重,可以让训练的焦点集中到难分类的样本上,最终得到的弱分类器的组合更容易得到更高的分类准确率。
可用
Dk+1
D_{k+1}
Dk+1
代表第k+1轮训练中,样本的权重集合,其中
Wk+1,1
W_{k+1,1}
Wk+1,1
代表第k+1轮中第一个样本的权重,以此类推:
Wk+1,N
W_{k+1,N}
Wk+1,N
代表第k+1轮中第N个样本的权重,公式:
Dk+1=(wk+1,1,wk+1,2,...,wk+1,N)
D_{k+1} = (w_{k+1,1}, w_{k+1,2}, ..., w_{k+1,N})
Dk+1=(wk+1,1,wk+1,2,...,wk+1,N)
第k+1轮中的样本权重,是根据该样本在第k轮的权重以及第k个分类器的准确率而定,具体的公式为:
wk+1,i=wk,iZkexp(−αkyiGk(xi)),i=1,2,...,N
w_{k+1,i} = \frac{w_{k,i}}{Z_k} \exp(-\alpha_k y_i G_k(x_i)), i = 1, 2, ..., N
wk+1,i=Zkwk,iexp(−αkyiGk(xi)),i=1,2,...,N
2 示例
有10个训练样本:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
现在我希望通过AdaBoost构建一个强分类器。
该怎么做呢?按照上面的AdaBoost工作原理,我们来模拟一下。
首先在第一轮训练中,我们得到10个样本的权重为1/10,即初始的10个样本权重一致,D1=(0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1)。
假设我有3个基础分类器:
f1(x)={1,x<2.5−1,x>2.5 f_1(x) = \begin{cases} 1, & x < 2.5 \\ -1, & x > 2.5 \end{cases} f1(x)={1,−1,x<2.5x>2.5
f2(x)={−1,x<5.51,x>5.5 f_2(x) = \begin{cases} -1, & x < 5.5 \\ 1, & x > 5.5 \end{cases} f2(x)={−1,1,x<5.5x>5.5
f3(x)={1,x<8.5−1,x>8.5 f_3(x) = \begin{cases} 1, & x < 8.5 \\ -1, & x > 8.5 \end{cases} f3(x)={1,−1,x<8.5x>8.5
可知分类器f1的错误率为0.3,即x取值6、7、8时分类错误;分类器f2的错误率为0.4,即x取值0、1、2、9时分类错误;分类器f3的错误率为0.3,即x取值为3、4、5时分类错误。
f1、f3分类器错误率最低,因此选f1或f3作最优分类器,若选f1,即第一轮训练得:
G1(x)={1,x≤2.5−1,x>2.5
G_1(x) =
\begin{cases}
1, & x \leq 2.5 \\
-1, & x > 2.5
\end{cases}
G1(x)={1,−1,x≤2.5x>2.5
按分类器权重公式得:
α1=12log1−e1e1=0.4236
\alpha_{1}=\frac{1}{2}\log\frac{1-e_{1}}{e_{1}}=0.4236
α1=21loge11−e1=0.4236
然后对下一轮的样本更新求权重值,代入
Wk+1,i
W_{k+1,i}
Wk+1,i
和
Dk+1
D_{k+1}
Dk+1
的公式,可得新的权重矩阵:D2=(0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。
第二轮训练继续统计三个分类器准确率,可得:
- f1错误率0.1666*3,即x取值为6、7、8时分类错误
- f2错误率为0.0715*4,即x取值为0、1、2、9时分类错误
- f3错误率为0.0715*3,即x取值3、4、5时分类错误
f3错误率最低,因此选f3作第二轮训练最优分类器:
G2(x)={1,x≤8.5−1,x>8.5
G_2(x) = \begin{cases}
1, & x \leq 8.5 \\
-1, & x > 8.5
\end{cases}
G2(x)={1,−1,x≤8.5x>8.5
按分类器权重公式得:
α2=12log1−e2e2=0.6496
\alpha_{2}=\frac{1}{2}\log\frac{1-e_{2}}{e_{2}}=0.6496
α2=21loge21−e2=0.6496
对下轮的样本更新求权重值,代入
Wk+1,i
W_{k+1,i}
Wk+1,i
和
Dk+1
D_{k+1}
Dk+1
的公式,得D3=(0.0455,0.0455,0.0455,0.1667, 0.1667,0.01667,0.1060, 0.1060, 0.1060, 0.0455)。
第三轮训练,继续统计三个分类器的准确率,可得:
- f1错误率0.1060*3,即x取值6、7、8时分类错误
- f2错误率为0.0455*4,即x取值为0、1、2、9时分类错误
- f3的错误率为0.1667*3,即x取值3、4、5时分类错误
f2错误率最低,因此选f2作第三轮训练的最优分类器:
G3(x)={−1,x<=5.51,x>5.5
G_3(x) = \begin{cases}
-1, & x <= 5.5 \\
1, & x > 5.5
\end{cases}
G3(x)={−1,1,x<=5.5x>5.5
我们根据分类器权重公式得到:
α3=12log1−e3e3=0.7514
\alpha _{3}=\frac{1}{2}\log \frac{1-e_{3}}{e_{3}}=0.7514
α3=21loge31−e3=0.7514
若只进行3轮训练,选择3个弱分类器,组合成一个强分类器,则最终的强分类器
G(x)=0.4236G1(x)+0.6496G2(x)+0.7514G3(x)
G(x) = 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)
G(x)=0.4236G1(x)+0.6496G2(x)+0.7514G3(x)
AdaBoost算法是个框架,你可指定任意分类器,通常用CART分类器作弱分类器。通过上面示例运算,体会AdaBoost计算流程即可。
3 总结
AdaBoost可理解为一种集成算法,通过训练不同弱分类器,集成起来形成一个强分类器。每轮训练都加入一个新的弱分类器,直到达到够低错误率或达到指定最大迭代次数。每次迭代都会引入一个新弱分类器(这个分类器是每一次迭代中计算出来的,是新的分类器,不是事先备好)。
在弱分类器的集合中,你不必担心弱分类器太弱了。实际上它只需要比随机猜测的效果略好一些即可。如果随机猜测的准确率是50%的话,那么每个弱分类器的准确率只要大于50%就可用。AdaBoost的强大在于迭代训练的机制,这样通过K个“臭皮匠”的组合也可以得到一个“诸葛亮”(强分类器)。
当然在每一轮的训练中,我们都需要从众多“臭皮匠”中选择一个拔尖的,也就是这一轮训练评比中的最优“臭皮匠”,对应的就是错误率最低的分类器。当然每一轮的样本的权重都会发生变化,这样做的目的是为了让之前错误分类的样本得到更多概率的重复训练机会。
同样原理也在日常,如善用错题本提升学习效率和成绩。
AdaBoost的核心思想
- 迭代训练: AdaBoost通过迭代的方式训练多个弱分类器。
- 加权组合: 将多个弱分类器按照其准确率赋予不同的权重,线性组合成一个强分类器。
- 样本权重更新: 在每一轮迭代中,对分类错误的样本赋予更高的权重,使得后续的分类器更加关注这些困难样本。
弱分类器与强分类器
- 弱分类器: 分类准确率仅比随机猜测略高的分类器。通常是简单模型,如决策树桩。
- 强分类器: 由多个弱分类器加权组合而成的分类器,具有很高的分类准确率。
AdaBoost训练过程
- 初始化样本权重: 给每个样本赋予相同的初始权重。
- 训练弱分类器: 基于当前样本分布,训练一个弱分类器。
- 计算分类错误率: 计算该弱分类器在当前样本分布下的分类错误率。
- 计算弱分类器的权重: 根据分类错误率计算该弱分类器的权重。
- 更新样本权重: 对于分类错误的样本,增加其权重;对于分类正确的样本,降低其权重。
- 组合弱分类器: 将得到的弱分类器按照权重线性组合,得到一个强分类器。
- 重复步骤2-6,直到达到预设的迭代次数或分类错误率满足要求。
为什么AdaBoost有效?
- 关注困难样本: 通过不断调整样本权重,AdaBoost能够重点关注那些难以分类的样本,从而提高模型的整体性能。
- 多样性: 每个弱分类器都关注不同的特征,通过组合这些弱分类器,可以得到一个更加鲁棒的模型。
- 逐步提升: AdaBoost是一种自适应算法,通过逐步迭代,不断提升模型的性能。
进一步思考
- 弱分类器的选择: AdaBoost对弱分类器的要求并不高,只要其准确率略高于随机猜测即可。常见的弱分类器包括决策树桩、神经网络等。
- 过拟合问题: 过多的迭代可能会导致过拟合,因此需要设置合适的迭代次数。
- 其他Boosting算法: 除了AdaBoost之外,还有其他的Boosting算法,如梯度提升树(GBDT)等。
本文由博客一文多发平台 OpenWrite 发布!
共同学习,写下你的评论
评论加载中...
作者其他优质文章