在开始训练神经网络之前,必须先初始化它们。不过,就像深度学习中的任何步骤一样,存在多种方法可以实现这一点。随机初始化神经权重就是其中一种方法。事实上,它经常被建议作为初始化神经网络的一种常见方法。
然而,这可能并非如此,因为存在两个问题:梯度消失现象和梯度爆炸现象。在这篇博客中,我们将探讨这些问题,并找到有效的方法来克服这些问题。
在我们能够进行下一步之前,我们必须简要回顾一下为何需要权重初始化。接下来我们将讨论随机初始化及其具体实现。一旦我们理解了神经网络的优化过程,我们就可以介绍这两个问题及其可能的解决方法。
权重初始化的重要性我一直认为,在我们再细说之前,有必要先说一点背景。
在这种情况下,问题是:问题在于为什么权重初始化一开始就是必要的?
简单来说,神经网络是由各种神经元组成的,这些神经元包括一个线性操作,即我称之为“向量点积加偏置”的操作,和一个非线性操作,称为“激活”。
在后者,也称为激活函数中,在线性操作的线性输出上添加了非线性。如果不这样做,神经网络将无法超越线性网络的表现——而过去几年取得的所有进步都将无法实现。
我们将在后面的博文中更深入地讲解激活函数(activation function)。
今天我们主要关注的是所谓的线性操作本身。在线性操作过程中,所谓的“输入向量”会与“权重向量”相乘,然后会将一个“偏置值”加到乘积结果上。让我们稍微拆解一下这些向量:
- “输入向量”与“权重向量”相乘;
-
然后加一个“偏置值”。
- 输入向量包含您当前提供给神经网络的样本。在第一层中,这是实际数据,在后续层中,它包含前一层神经元的输出。
- 权重向量包含了神经元从数据中学到的独特模式。这实际上就是神经网络学习的方式:因为每个神经元都能学习数据中隐藏的某些模式,整个网络可以识别出许多这样的模式。
然而,在训练过程开始之前,所有的权重向量必须被初始化为某些数值。它们不能是空的向量,因为空向量无法进行有效的乘法运算。正如你可能已经猜到的那样,存在多种初始化方法……其中最广为人知的一种是随机初始化。
随机初始化(也就是随机开始)正如其名,随机初始化就是随机设置权重。
随机初始化有两种方式:一种是通过正态分布,另一种是通过均匀分布。
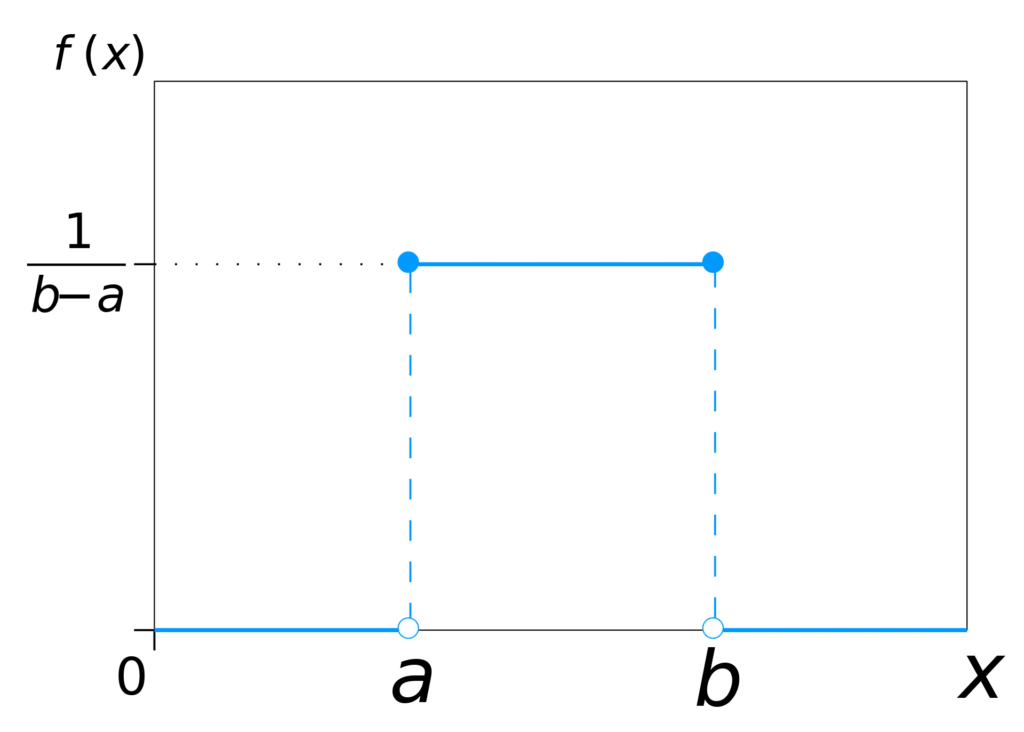
均匀分布这指的是,均匀分布:
均匀分布。感谢这位作者,其作品来自维基百科:© IkamusumeFan(用户名)依据CC BY-SA 3.0许可协议。
不要害怕,其实这很简单。
你看到的是均匀分布的概率,简单来说:当我随机抽取一个数时,这个数落在 a <= x <= b 范围内的概率为 1/(b-a),而落在该范围之外的概率则是 0。
有趣的是:这实际上是一个连续分布。也就是说,在上面提到的区间内有无限多个实数。因此,找到某个特定的数字的概率实际上是0。可以在这里了解更多原因。可以在这里了解更多原因。
一般情况下,在为深度学习配置均匀分布时,可以设置以下变量,例如:
- 应选择的最小值。
- 应选择的最大值。
- 一个用于固定随机数生成器的种子数。因此,有时需要固定随机数生成器的种子,因为随机数生成器并不是真正的随机;它们是伪随机。这样,每次使用生成器时,你希望它具有相同的伪随机性质(即与真正随机性不同的偏差),否则每次生成的权重可能会有不同的伪随机性质。
在这个情况下,最大值是b,而不是a。
正态这是所谓的正态分布。
感谢:Inductiveload at Wikipedia.
像均匀分布一样,正态分布也是一种连续的概率分布。
事实上,它是一种应用最广泛的概率分布之一;只要配置得当,许多自然现象都可以通过这种分布来描述。
具体来说,可以配置均值和标准差的值,并再次将(伪)随机数生成器设定为特定种子。
如果你学过统计,你应该知道平均数和标准差是什么。如果没有的话,可以在这里查看:http://www.ltcconline.net/greenl/courses/201/descstat/mean.htm。
你知道吗?与均匀分布相比,均匀分布需要你手动配置可能值的范围,而在正态分布(也叫高斯分布)中你不需要配置。
理论上来说,这意味着理论上你可以找到任何实数作为结果。然而,如上图(例如以红色显示的标准正态分布)所示,你的数字大概率会落在负3到正3范围内。
要选择哪个发行版呢?既然你知道均匀分布(uniform distribution)和正态分布(normal distribution)都在深度神经网络中经常被使用,你可能就会想:那我应该用哪个分布比较好呢?
当然,如果你随意将它们随机初始化也行。
在数据科学StackExchange上的帖子中,有人回答了这个问题:看来这其实无关紧要。
或者说,哪个更好这一点并不清楚。
实际上,在Glorot和He的“初始化论文”里,文章的作者认为,在讨论随机初始化问题时,Glorot等人和He等人使用了两种不同的初始化方法:Glorot的方法使用均匀分布,而He的方法则使用正态分布。
似乎选择一种随机的统计分布方式来初始化权重取决于你自己。
但是,随机初始化在某些条件下可能会导致问题:你可能会遇到梯度消失和梯度爆炸的问题。在介绍这些问题前,我们先简要看看大多数神经网络是如何被优化的。
神经网络的优化过程:梯度下降和反向传播当你在训练一个神经网络时,你实际上是提供数据给它,让它会进行预测,然后计算误差,也就是损失。
这叫做数据的前向传播。
现在,你可以将损失视为一个数学上的函数,这个函数能很好地体现你的数据特点。换句话说,我们可以找到这个函数的最小值,从而优化它。
模型在哪种情况下表现最佳?当然是在损失最小时。
计算梯度值通过计算损失函数的导数(梯度),你可以得到一个用于改进神经网络最终隐藏层的梯度。将权重稍微调整到梯度的方向,你的模型将向损失最小值的方向迈出一小步,从而得到一点改进。
我们称其为梯度下降法,通常使用随机版本。
梯度链接不过,神经网络包含多个层次,而不仅仅是一层。
我们不能简单地对倒数第二层的梯度进行求解,因为它与最后一层紧密相连。因此,在计算这一层的梯度时,你需要考虑到损失函数梯度。
对于下一层,你需要重复这个步骤,但还需要加入倒数第二隐藏层。
等等。
你实际上是在创建一个梯度的链条,然后乘以它们,以找到让当前层更好的梯度。
我们把它叫做反向传播。
比如,优化一个神经网络优化过程主要包括:
- 数据的前向传递,计算误差或 损失。
逆向传递数据,以此计算改进
- 用于计算希望优化的层的梯度的反向传播。
- (随机) 梯度下降法或更高级的优化器,它们利用梯度将神经网络的权重调整到正确的方向,从而沿着“损失的山谷”向下走。
当你把不同层的梯度相乘来计算某一层的梯度时,你会发现一个奇怪的现象:所谓的梯度消失。
如你从正态分布中可以看到,例如,大多数值相对较低,比如说在+3和-1之间。事实上,随机选取一个数,这个数在-1和1之间(例如,-0.9999999999 < x < 0.9999999999...)的可能性最大。
假设所有的神经元输出为 0.1 —— 这有点奇怪,但这样可以帮助我们更容易地理解梯度消失的情况。假设你有一些层,并且梯度改进为 0.03。向上追溯五层,激活函数的输出范围在 0 到 1 之间,那么第六层的梯度改进可能近似为 0.1 x 0.1 x 0.1 x 0.1 x 0.1 x 0.03。
那真是一个小数目。
梯度消失的问题意味着你的最前面的层学习会非常慢,因为梯度是按链式传递的,导致梯度非常小。
实践中,这可能意味着你需要无限的时间和计算资源来找到最优化的值,也就是最小的损失。
而且我们根本就不想要那个——我们想要最好的模型。
梯度爆炸现象训练过程中也可能遇到“梯度爆炸”问题。本质上,某些神经元因为数值过大(即溢出)而失效。
这是怎么回事?
假设你随机初始化权重的话,你选择哪种初始化方法其实并不重要。你可以想象,在前向传播时,随机权重很可能导致非常大的损失,仅仅是因为它与底层数据分布完全不匹配。
发生了什么?权重的摆动,或者说梯度,可能会非常大。尤其是在随机数大于1或小于-1时,这种情况尤其明显。由于正常的输出链接过程,我们遇到了麻烦。我们发现的数字不是越来越小,而是越来越大了。
最终导致数值溢出错误,结果会出现“非数字”(NaN)。影响:你的学习过程会因此受到严重影响。
这些问题我们该怎么做?幸好,我们找到了一个解决办法。多亏了一些科学家——特别是那些从事Glorot和He研究的科学家们——更高级的初始化方法已经被找到,这些方法可能有助于缓解梯度消失及梯度爆炸的问题。
Xavier 和 He 初始化这些初始化器,如Xavier(或Glorot)和He,通常被称为,在例如Keras中可用,实际上,它们只做了一件事:它们确保权重被设置为接近1的值。(我们将在以后的帖子中进一步讨论这些初始化器。)
这样一来,问题就大大减少了。
它们在调整权重以达到接近1的方式上有所不同。因此,它们通常需要配合不同的激活函数使用。具体来说,He初始化是专门为ReLU激活网络设计的,最适合用于这种类型的网络。对于其他类型的网络,Xavier(或Glorot)初始化通常效果最佳。
做实验尽管所有这些在理论上有效的缓解技术,对于数据科学及其相关的机器学习项目来说,有一条建议总是适用的:多做实验!
看看哪些有效,哪些无效——并根据实际情况调整你的方法。同时,试着搞清楚黑箱内部的状况,从观察中总结出可以以后再用的通用经验。
简单来说,理论固然重要,但关键是要适合你自己,而唯一的方法就是通过实践来掌握。
简介在这篇博客里,我们了解了随机初始化的工作原理,以及为什么它比全零初始化更好。我们也明白了使用随机初始化的原因。然而,我们也遇到了一些随机初始化的基本问题,即梯度消失和梯度爆炸问题,这两个问题是随机初始化过程中常见的问题。通过使用更高级的初始化方法,比如He初始化和Xavier(或Glorot)初始化,我们最终可以避免这些问题,并获得一个性能良好的模型。
希望你今天从这篇帖子中学到了一些东西。欢迎任何评论、问题或分享。谢谢阅读。
参考Alese, E. (2018年6月10日). 消失和爆炸梯度的有趣案例。参见 https://medium.com/learn-love-ai/the-curious-case-of-the-vanishing-exploding-gradient-bf58ec6822eb
Glorot, X., & Bengio, Y. (2019). 理解训练深度前馈神经网络的困难. 在意大利撒丁岛举行的国际人工智能与统计会议上提出的论文。
他,K.,张,X.,任,S.,孙,J.(2015)。深入研究整流器:在ImageNet分类任务中超越人类水平的表现力。2015年IEEE国际计算机视觉大会(ICCV)。doi:10.1109/iccv.2015.123
Keras. (n.d.). 初始化. 详见 https://keras.io/initializers/
何时使用(He 或 Glorot)正态初始化而非均匀初始化?它在批量标准化中的影响如何?(日期不详)。来源自 https://datascience.stackexchange.com/questions/13061/when-to-use-he-or-glorot-normal-initialization-over-uniform-init-and-what-are/13362#13362
Yadav, S. (2018年11月9日). 神经网络中的权重初始化技术,来源:https://towardsdatascience.com/weight-initialization-techniques-in-neural-networks-26c649eb3b78
共同学习,写下你的评论
评论加载中...
作者其他优质文章