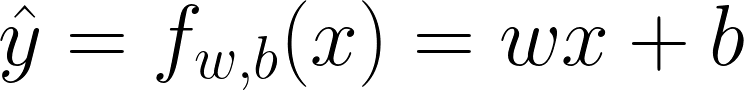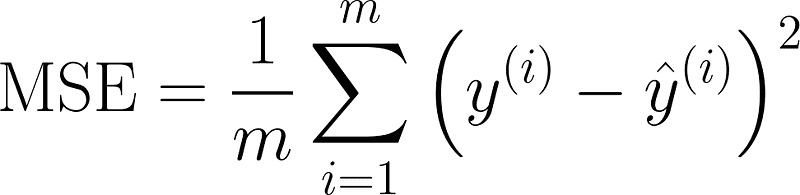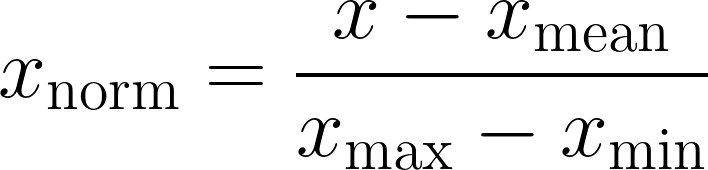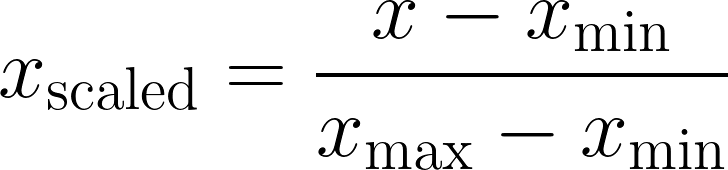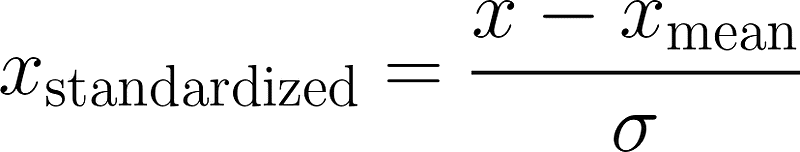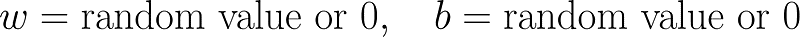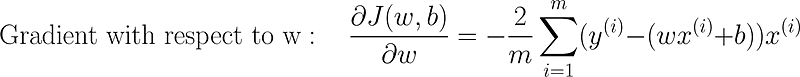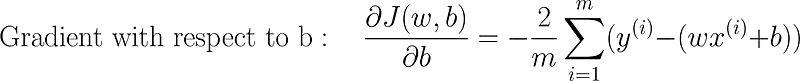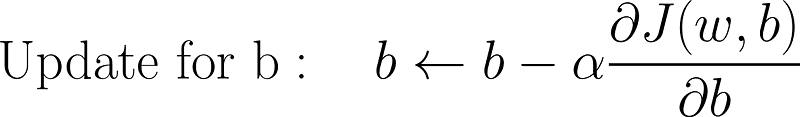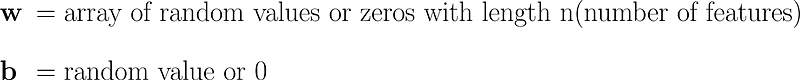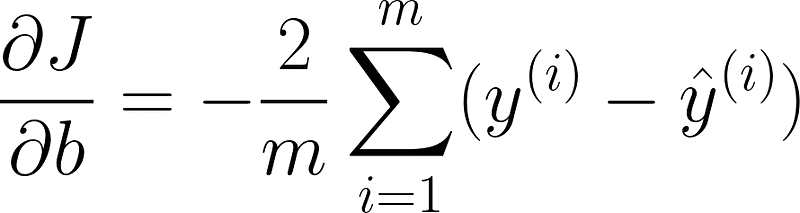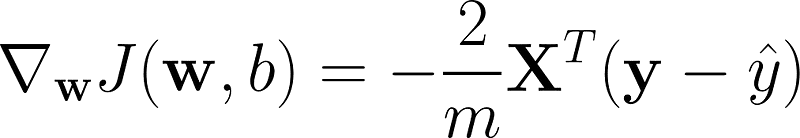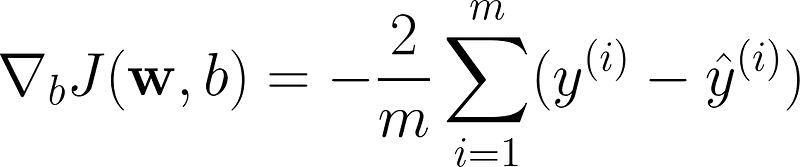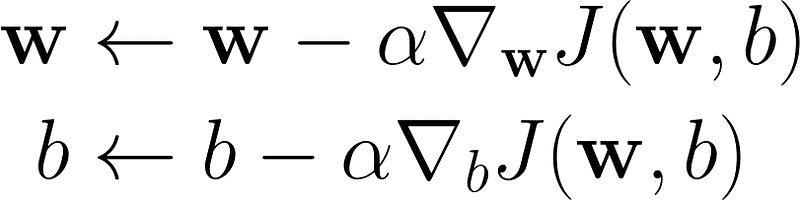在这篇指南里,我们将解释线性回归及其工作原理,并一步步带你完成全过程。我们还会介绍特征缩放和梯度下降,这些都是提高模型准确性的关键技巧。不论你是分析商业趋势还是研究数据科学,这篇指南都是个很好的开始。
内容列表
- 概述
- 了解监督学习
- 什么是线性回归?
- 一元线性回归
- 多元线性回归模型
- 成本函数
- 特征缩放
- 梯度下降法
- 一元线性回归中的梯度下降
-
多元线性回归中的梯度下降
-
- *
线性回归是一个简单却强大的工具,用来了解不同因素之间的关系并进行预测。例如,你可能想知道学习时间如何影响考试成绩,或者根据房屋大小和位置预测售价,或者增加广告投入对提高销售额的影响。线性回归允许我们分析数据点,比如学习时间或广告投入,并画出一条最能预测结果的直线,如考试成绩或销量。这项技术在很多领域都非常有用,帮助我们根据数据做出明智的决定。
了解监督学习在深入探讨线性回归之前,理解监督学习这一使用标注数据训练模型的机器学习方法是十分必要的。在监督学习中,我们会向模型提供带有特征(输入变量)及其对应标签(正确输出)的训练数据。
主要有两种监督学习任务:
- 回归:这预测一个连续值,范围可以是无限的。例如,根据各种特征预测房价。
- 分类:这与回归不同,分类任务预测的是有限类别中的一个类别。例如,判断一封邮件是否为垃圾邮件,比如。
线性回归是一种在统计学和机器学习中应用的监督学习方法,用于理解自变量(我们认为会影响结果的因素)和因变量(我们想要预测的结果)之间的关系。比如,当我们想了解一些因素如何影响一个结果时,我们就可以用线性回归。这些因素就是自变量,结果就是因变量。
目标是找到一条最合适的拟合线来表示这种关系,这条线用一个线性方程来描述。通过分析标记的数据(具有已知结果的数据),线性回归分析帮助我们理解自变量的变化如何影响因变量的变化。
术语列表简单线性回归是用来分析一个因变量和一个自变量之间关系的。它旨在通过建立这种关系的模型来拟合一条直线,这关系可以用如下的方程来表示:
在这个方程中:
- y_hat(或 f_wb(x)):我们预测的结果,也就是因变量。
- b : 这是回归线的截距,表示当自变量 x 为零时,因变量 y 的预估值。
- w : 这是自变量 x 的系数,表示每增加 x 一个单位,因变量 y_hat 会如何变化。
- x : 这是自变量,作为模型的预测变量,用来估计 y_hat 的值。
多元线性回归扩展了简单线性回归的概念,通过研究一个因变量和两个或多个自变量之间的关系。这种方法使我们能够建立更复杂的关系模型,并了解多个因素如何影响结果。
请参见图中的多元线性回归公式。
位置:
- n 总特征数(自变量数)
成本函数,也称为损失函数,量化了期望(真实)值与模型预测值之间的差异。它衡量模型在给定数据集上的表现,。在简单的线性回归模型中,最常用的就是均方误差。
地点:
- m 是训练样本数
- y_hat (预测值)是预测值
- y (实际值或期望值)是实际值或期望值
特征缩放是至关重要的一步,在数据预处理中,特别是在使用依赖距离计算或梯度下降优化的算法时,例如线性回归、逻辑回归和支持向量机。特征缩放的目的在于将数据中的特征范围标准化,以确保它们在模型学习过程中贡献相等。
一些常用的特征缩放方法
平均值标准化
均值化涉及调整特征的数值,让它们的平均值为零。
特性
- 数据范围大约在[-1,1]或接近这个范围。
- 对异常值非常敏感,这可能导致均值偏移,进而影响归一化处理。
应用场景
- 线性回归:有助于训练过程中的收敛性。
- 基于梯度的算法:神经网络和其他基于梯度的算法在数据以零为中心时通常收敛得更快。
- 无明显离群点的数据集:特别适合那些数值范围相近且几乎没有极端离群点的数据集。
最小-最大标准化
最小-最大标准化是一种将特征重新缩放到固定区间的方法,通常为[0,1]或[−1,1]这两个区间。
特色
- 固定范围缩放:将数据缩放到特定范围内,例如,通常为[0,1]。
- 对异常值的敏感性:它很容易受到异常值的显著影响,从而扭曲其他值的缩放效果。
应用场景
- 图像处理:通常在深度学习模型中使用,如卷积神经网络(CNN),像素值通常被缩放至[0,1]区间。
- 基于距离的算法:对于依赖距离计算的算法(如k近邻算法(KNN)、k均值聚类和支撑向量机(SVM))至关重要,以确保所有特征的贡献是相同的。
- 基于树的模型:虽然与基于树的模型(如决策树和随机森林)相比,对于其他算法来说相对不那么重要,但在特征尺度差异极大的情况下,仍然可以发挥一定的帮助作用。
Z分数标准
Z分数标准化(也称为标准缩放),将特征转换为均值为零、标准差为一的状态。这种技术对假设数据是正态分布的算法特别有用。
地点
- sigma,通常称为“偏差”,是该特征值的标准偏差。
特色:
- 均值中心化:以零为中心调整数据。
- 单位方差:使标准差为一。
- 对异常值的稳健性:相比于最小-最大缩放,对异常值更稳健,但仍对极端异常值敏感。
应用场景:
- 神经网络:提高性能和加快训练时的收敛。
- 主成分分析(PCA) 和 线性判别分析(LDA):需要这些技术来确保所有特征的贡献相等。
- 高斯朴素贝叶斯:通过归一化输入特征来提升分类性能。
弹性扩展
这是一种基于中位数和四分位间距(IQR)来缩放特征的技术。这种方法特别适合处理含有显著异常值的数据集,因为它能有效降低异常值对最终缩放结果的影响。
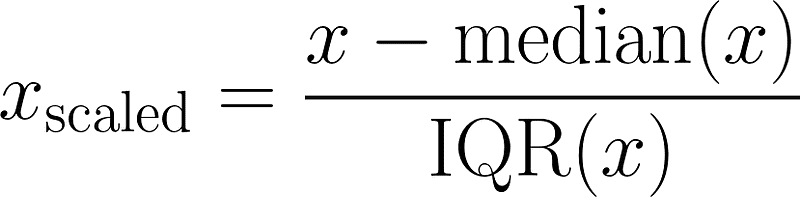
地点:
- IQR(x) 是训练集中第75和第25百分位数之间的差值
特色
- 以中位数为中心:使数据以中位数而非平均数为中心,使其更具抗异常值的特性。
- 四分位间距 (IQR):使用四分位间距 (IQR) 对数据进行缩放,它是训练数据中第 75 百分位数 (Q3) 和第 25 百分位数 (Q1) 的差值。这有助于保持分布的稳定性。
应用场景
- 含离群点的数据:在这种情况下效果良好。
- 金融:在金融数据中特别有用,即使这些数据中包含极端值。
- 环境数据:特别适合于环境数据集,因为这些数据集的测量范围可能非常广泛。
梯度下降是一种强大的优化算法,常用于训练机器学习模型,比如线性回归。其主要目标是将预期值与预测值之间的误差最小化。
最初,成本函数在初始点的斜率可能很陡峭。随着算法迭代并更新参数,引导模型逐渐接近成本函数的最低点,也就是我们常说的收敛点或局部最小值。在该收敛点,成本函数达到最小值,表明模型的预测尽可能接近实际情况。一旦参数达到这一点,进一步的参数调整只会带来微小的变化,说明优化过程已经找到最适合数据的最佳参数。
以下是该过程中的重要步骤,
- 初始化:模型参数(例如截距 b 和系数 w)从随机值开始初始化。
- 计算梯度:计算相对于模型参数的成本函数梯度。这个梯度表示成本函数变化的方向和速率。
- 更新参数:沿着梯度的相反方向调整模型参数以减少误差。更新规则如下:
- 迭代:重复该过程,直到成本函数的变化很小或达到指定的迭代次数。
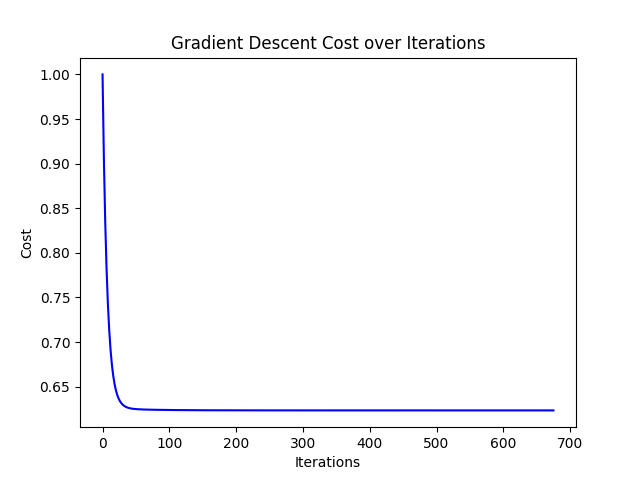
小贴士:画出x轴为迭代次数,y轴为成本的图表。如果图表呈现出平滑下降的趋势,那么你的实现大概率是正确的。
几种梯度下降
批量梯度下降算法
- 优势:由于使用了整个数据集,因此可以提供稳定的且准确的梯度估计。对于凸函数,可以直接收敛到全局最小值。
- 劣势:对于大型数据集可能非常慢,因为它每次迭代都要处理所有样本。
- 应用场景:通常用于数据集小到可以轻松加载到内存中的场景,例如线性回归或在表格数据上的逻辑回归模型。
随机梯度下降(SGD),也就是随机梯度下降法
- 优点:由于它一次处理一个样本,因此更新更快,可能更快地达到稳定状态。由于其内在噪声特性,它可以帮助逃离局部最小值。
- 缺点:收敛过程更加震荡,可能在最小值周围振荡。
- 应用场景:常应用于在线学习、实时预测,或处理不能一次性处理的大型数据集(例如,在图像数据上训练神经网络)。
小批量梯度下降法(MBD)
- 优点:结合了批量梯度下降和随机梯度下降的优点。相较于批量梯度下降,它收敛更快;相比随机梯度下降,它收敛更稳定。它还可以利用向量化进行高效计算。
- 缺点:选择小批量数据的大小可能具有挑战性,并可能影响收敛速度和稳定性。
- 应用场景:常用于深度学习应用,特别是在大型数据集上的训练,例如,在卷积神经网络(CNN)中进行的图像分类任务,或自然语言处理模型的训练。
梯度下降法步骤:线性回归
- 给模型参数初始化 可以随机选择或设为零的初始值来初始化模型参数。
- 计算梯度 计算损失函数关于模型的参数的梯度。梯度表示损失函数变化的方向和速率。
- 更新参数 通过与梯度相反的方向调整模型的参数来减少错误。更新规则如下:
在简单线性回归中的梯度下降参数更新
在哪:,
- J(w, b) 是成本函数,即上述提到的均方误差(MSE)。
- Alpha 是学习率,一个介于 0 和 1 之间的较小正数。它控制梯度下降过程中每次下降的步长大小,以达到收敛点或局部最小值。
提示: 从一个小的学习速率(例如 0.01)开始,并逐步增加。如果成本平稳地下降,说明这个学习率是好的。如果成本波动或发散,应减小学习速率。学习速率过大可能会导致梯度下降过冲,无法找到最小值并且无法收敛。
- 迭代:反复执行该过程,直到成本函数的变化很小或不再显著,或者达到预定的迭代次数。
(Note: Considering the expert suggestions and the context, the translation can be simplified and directly stated as "多元线性回归中的梯度下降" for more colloquial and precise usage. However, to explicitly follow the original request to retain the structure while applying the suggestions, the provided translation reflects a balanced approach between formality and fluency.)
多元线性回归中的梯度下降多变量线性回归中的梯度下降步骤
- 初始化 从随机值初始化每个参数(包括截距b和每个特征的权重w)。给截距b和每个特征的权重w赋随机初始值。
- 计算梯度 算一下模型参数的梯度(成本函数或损失函数)。
在多个变量的线性回归中,使用梯度下降计算梯度.
向量表示
地点:
- x_{j}^{i} 是第 i 个训练样本的第 j 个特征值
- x^{T} 是 x 的转置
- 更新参数 将模型参数沿与梯度相反的方向调整以减少误差。更新公式为:
- 迭代 反复该过程,直到成本函数的变化变得很小或达到指定的迭代次数。
这是使用Python实现的简单线性回归模型的梯度下降算法[https://github.com/mohiyaddeen7/MachineLearning/blob/main/Linear%20Regression/MultipleLinearRegression.py?source=post_page-----031e4f3dc08c--------------------------------]
总结
祝贺!! 💫 在这篇文章中,我们探讨了线性回归和多元线性回归的基础知识,介绍了如何实现梯度下降,讨论了像特征缩放这样的关键技术来优化模型性能。通过学习如何初始化模型参数、计算梯度以及迭代更新权重,你现在可以运用线性回归算法,并在实际数据集上提升其性能。
无论你是处理简单的线性回归问题还是面对多个特征,掌握梯度下降并理解其核心概念将大大提高你开发高效机器学习模型的能力。不断尝试,提升技能,拥抱学习过程——这其实和结果一样重要!
更多精彩关于机器学习技巧和 web 开发主题的内容等着你。在探索和构建更智能模型的过程中,愿你学习愉快! 💫
让我们在 LinkedIn 上联系 🚀
这篇文章最初发表在我的Medium博客(链接)上,我在那里分享更多关于数据分析、机器学习和编程的心得。欢迎去看一看,也欢迎在Medium上关注我,获取更多精彩相关资讯。
请点赞、分享,然后关注我们 🙏.
欢迎在评论区提问,你提出的问题随时欢迎提出,我会尽快详细回答你的问题。你的疑问会得到及时且全面的回复。❤️
共同学习,写下你的评论
评论加载中...
作者其他优质文章