从Logistic回归到神经网络

1 线性回归 (Linear Regression)

大略总结下

回归来源

我们关心的东西没有办法用一个或多个变量确定的表示，即无函数关系；但是又存在着较强的关联性。这种关系就叫统计关系或相关关系。衍生两个分支是回归分析和相关分析。二者侧重不同，回归分析用的更广泛。 
回归分析中，x称为解释变量，是非随机变量；y称为响应变量，是随机变量。 
回归有线性回归和非线性回归；以最小二乘法(Least Square)为主的线性回归是最经典的回归模型。 
回归和分类的问题是相同的，仅区别于响应变量的形式。y是分类变量时(例：0-1），模型为分类；是连续变量时称为回归。

线性回归总结

Gauss-Markov 假设：

高斯-马尔科夫是核心假设，后面回归出现的问题都由此而来。

1. 线性模型成立  , 是常系数，是随机误差项。

2. 样本(sample) 是随机抽样得到。

3. 解释变量不为常数，没有共线性（一个变量不能由其他变量线性表示）

4. 误差项不相关：

5. 误差项同方差: 是常数。

常见问题及解决办法

• 异方差性：即GM假设第5条不满足，不再是常数。解决办法：加权最小二乘。打个广告，解决异方差性，这篇推送写的不错：如何收服异方差性

• 多重共线性：第3条不满足。举例：自变量同时有一天进食量和中午以后进食量。解决办法：根据多重共线性检验删除一些不重要的变量；逐步回归、主成分回归、偏最小二乘，Ridge,Lasso（岭回归与LASSO为正则化方法，在解释性上强于前面两种） 
  

• 当响应变量是定性变量。解决办法：

• 在数据处理上设置哑变量(dummy variable)

• 响应变量是定性变量在生活中有广泛的应用，其属于广义线性模型(generialized linear model,GLM)的研究范畴。

2 感知机 (Perceptron)

定义

当响应变量  是分类变量时，建模过程就是分类了。感知机(Perceptron)是二分类的线性分类模型。可以看做是线性回归的兄弟（线性分类)。同时也是神经网络和支持向量机(support vector machine)的基础。 
下一篇学习笔记会试着写写从感知机到支持向量机。

在周志华老师的机器学习一书中侧重于将其作为神经网络的基础概念，对感知机的定义如下：

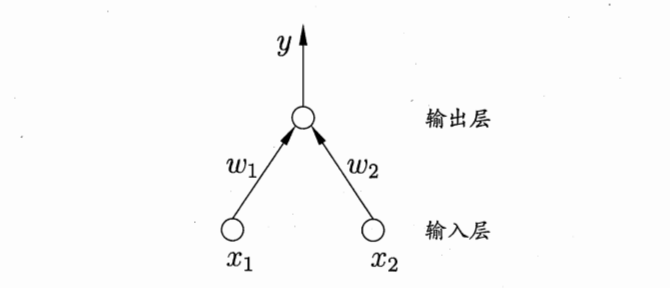
感知机由两层神经元组成，输入层接受外界输入信号后传递给输出层，输出层是M-P神经元，亦称“阈值逻辑单元”(threshold logic unit)。如下图所示：

学习策略

在感知机模型中，假设数据集是线性可分的。因此，感知机的目标是找到一个超平面，将两类点(正 or 负)完全分隔开来。因此，学习策略的核心是找到这样的超平面方程：

因此，训练需要得到的参数是  和 。采用误分类点到该超平面的距离来作为损失函数；这里不选误分类点的总个数是因为这样的损失函数不是参数  和 的连续可导函数，不便于优化。

损失函数：

其中是误分类点的集合。这个损失函数就是感知机学习的经验风险函数；所以问题就转化为一个求解损失函数最小的最优化问题，最优化的方法是随机梯度下降(Stochastic gradient descent)。对于更多细节可以看李航的统计学习方法这本书；感知机这部分在书中有很全面的介绍。

3 Logistic Regression

怎么来的

在前面已经提到了广义线性模型，其一般表示形式为： 

其中，函数 称为连接函数(link funtion)，且要求是单调可微的。广义线性模型中，要求响应变量  服从指数分布族中的已知分布。常见的正态分布、泊松分布、二项分布等都属于指数分布族。 
那为什么要求服从指数分布族呢? 
个人认为：如果我们这样求出来的一个值，而不知道被解释变量的分布情况，没啥用，什么也干不了。 (欢迎大佬补充)

因此在Logistic回归中，取连接函数为函数：， 
当,相应的模型为： 

那大佬们说的Sigmoid函数是什么意思呢？ 
我们将上式写成回归函数的样子(两边取指数，挪一挪就得了): 

机器学习中，一般令  ，且有 ，其中 。 
我们称  为 Sigmoid函数，图像长这个样子：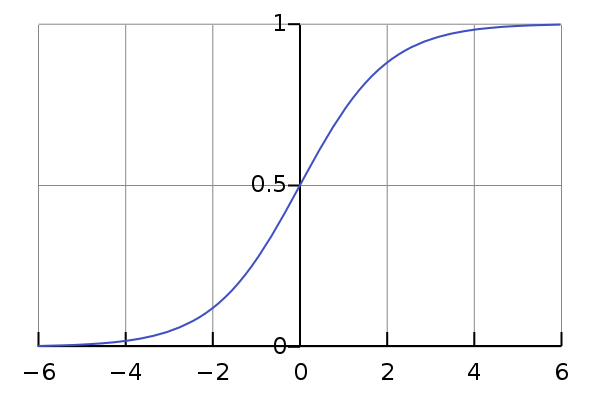 
 
可以看到函数图像是一个 S型 的曲线，它将线性模型 非线性映射到  区间里。 
因此可以简单的认为：Logistic回归分两个部分，第一部分线性回归形式 ，第二部分是非线性映射 

怎么求解

首先介绍一下常见的几种损失函数 :

1. 平方损失： 
   

   
   很容易发现，我们普通最小二乘回归所用的的损失函数就是平方损失。带了平方项，使得残差累计不能够正负抵消，且损失函数是连续可导的凸函数：求起来也比较容易，局部最小就是全局最小。

   
   

2. 绝对值损失 
   

   
   当回归用绝对值损失时，则称为最小一乘回归，它使得残差绝对值的和最小。最小一乘回归是分位数回归(quantile regression)的特例。

   
   

3. LASSO损失 
   

   
   给损失函数加了参数  的一范数作为惩罚项。

   
   

Logistic回归的损失函数:负对数损失

我们已经得到了Logistic回归模型，等式左边的  是在已有的信息  下， 等于 1 的概率作为响应变量 。那么就有  。为了使用 极大似然估计 (Maximum Likelihood Estimate) 来估计参数  和  , 我们写出其似然函数： 

即：当  时，(1-y) =0 ，任何式子的 0 幂次都等于0 ，等式取第一个；当  时， ，任何式子的 0 幂次都等于0 ，等式取第二个。 
由于 为单调增函数，不改变损失函数的极大值点 ，且将幂运算变为乘法，简化计算，所以似然项可重写为:

极大似然估计要使上式最大化，得到参数  。最优化理论中，我们习惯求解极小化问题，所以添个负号，变为找最小值的优化问题。

这个时候损失函数是高阶可导的连续凸函数，梯度下降法就可以求解了。

Tips

统计中关心的 比值  和 比值的比：优势比( )

比值代表 正样本的概率 除以 负样本的概率，使得原来  上的取值 放大到了 0到正无穷；且使二者分得更开。若在取个对数，得到  ,值域从0到正无穷 扩大到 负无穷到正无穷，吻合一般的线性模型对响应变量的要求。

优势比经常被用来解释变量的变动带来的事件风险变化。

参加交大研究夏令营面试的时候，一位生物统计的老师问到这个，当时有点懵圈，因为上课的时候老师也没咋讲。诶，想学生物统计的还是把这一块好好了解一下吧。

4 神经网络 (Neural Network)

怎么理解

神经元: 

 

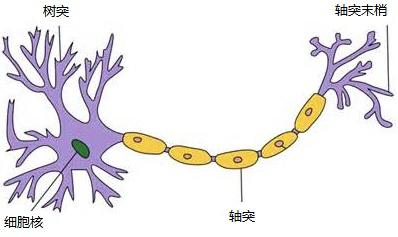
上图是一个神经元，高中生物学过。简要来说：树突接受信号，胞体处理信号，如果信号产生的电位达到阈值(threshold)，胞体变为“兴奋”状态(激活状态)，通过轴突给下一个神经元传出信号。

神经元模型：

在机器学习中，谈论神经网络时指的是 “神经网络学习“，是机器学习和生物神经网络的交叉部分。

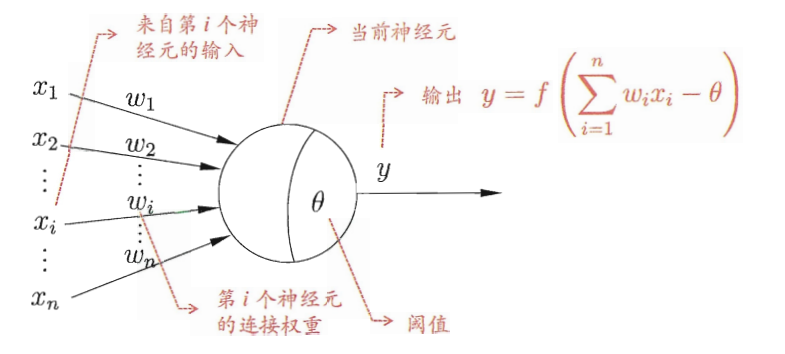
神经元模型是神经网络学习中最基本的成分。下图可以抽象的看做神经元模型，和上面的生物神经元对照着看。

左边的对应数据的输入（树突结构信号的传入），圆圈相当于胞体结构，胞体得到信息后和阈值做比较(代表阈值);最后通过激活函数(activation function)决定输出 . 
举个例子：用手挠一下神经元，可能强度达不到阈值，神经元不理你；如果你用针用力刺一下它，疼痛感立马大于阈值，神经元分泌化学物质，即输出相应的信号。

最简单的几种形式

感知机

前面介绍了感知机，它可以看做是两层神经元组成，激活函数是 Heaviside函数(阶跃函数)的神经元模型。当输入信号大于阈值，神经元兴奋，输出1；否则神经元抑制，输出 0。

Logistic回归

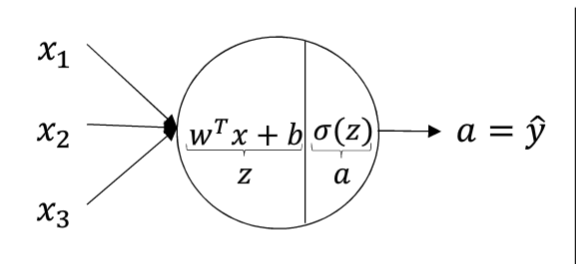
Logistic回归可以看做是两层神经元，激活函数是Sigmoid函数的神经网络。

正如前面所说，可以给Logistic回归看做两步骤，第一：，第二：  。

后记

原文出处