决策树不仅限于对数据进行分类——它们同样擅长预测数值!分类树常常更受关注,但回归树(或称为决策树回归器)在连续变量预测领域中是非常强大的工具。
我们将讨论回归树构建的机制(这些机制与分类树相似),在此处,我们将不仅讨论之前在分类器文章中提到的预剪枝方法,例如“最小样本叶”和“最大树深度”。我们将探讨最常用的后剪枝方法,即成本复杂度剪枝,这种方法在决策树的成本函数中引入了一个复杂性参数,从而实现成本复杂性剪枝。
所有视觉内容:使用Canva Pro制作。已优化移动设备上的显示;在桌面设备上可能看起来过大。
这是定义
回归决策树是一种通过树形结构预测数值的模型。它从根节点开始逐步分裂,根据关键特征将数据进行分割。每个节点询问一个特征,进一步划分数据,直到达到带有最终预测值的叶节点。为了得到结果,只需从根节点到叶节点跟随与你的数据特征相匹配的路径。
回归决策树通过一系列基于数据的问题来预测数值结果,最终得出一个数值。
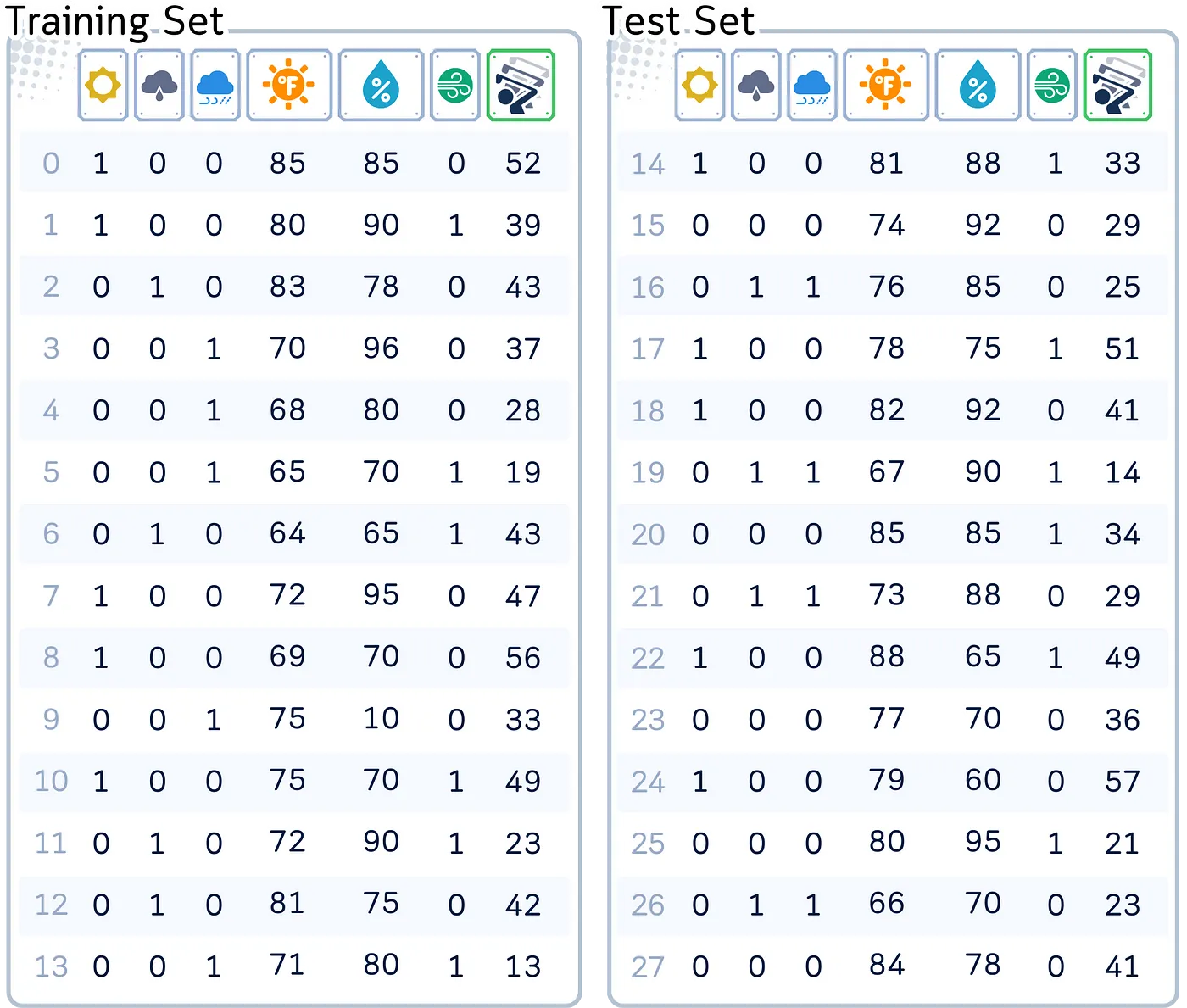
📊 数据集:使用的数据集为了演示我们的概念,我们用一个标准数据集,这个数据集用来预测来打高尔夫的人数,考虑了天气、温度、湿度和风的情况。
列:‘Outlook’(一个独热编码,表示为 sunny, overcast, rain),‘Temperature’(华氏温度),‘Humidity’(湿度的百分比),‘Wind’(Yes/No)和 ‘Number of Players’(数值型,即目标特征)
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
# 创建数据集
dataset_dict = {
'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
'Temp.': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
'Humid.': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
df = pd.DataFrame(dataset_dict)
# 将 'Outlook' 列进行 one-hot 编码
df = pd.get_dummies(df, columns=['Outlook'],prefix='',prefix_sep='')
# 将 'Wind' 列转换为二值
df['Wind'] = df['Wind'].astype(int)
# 拆分数据为特征和目标,再划分为训练集和测试集
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)回归决策树通过递归地根据能最好减少预测误差的特征来分割数据。具体流程如下:
- 从整个数据集开始,从根节点开始。
- 选择一个可以最小化特定错误度量(如均方误差或方差)的特征来分割数据。
- 根据分割结果创建相应特征值的子节点,每个子节点代表与相应特征值匹配的数据子集。
- 对每个子节点重复步骤2-3,继续分割数据,直到满足停止条件为止。
- 为每个叶节点分配一个最终预测值,通常为该节点中目标值的平均值。
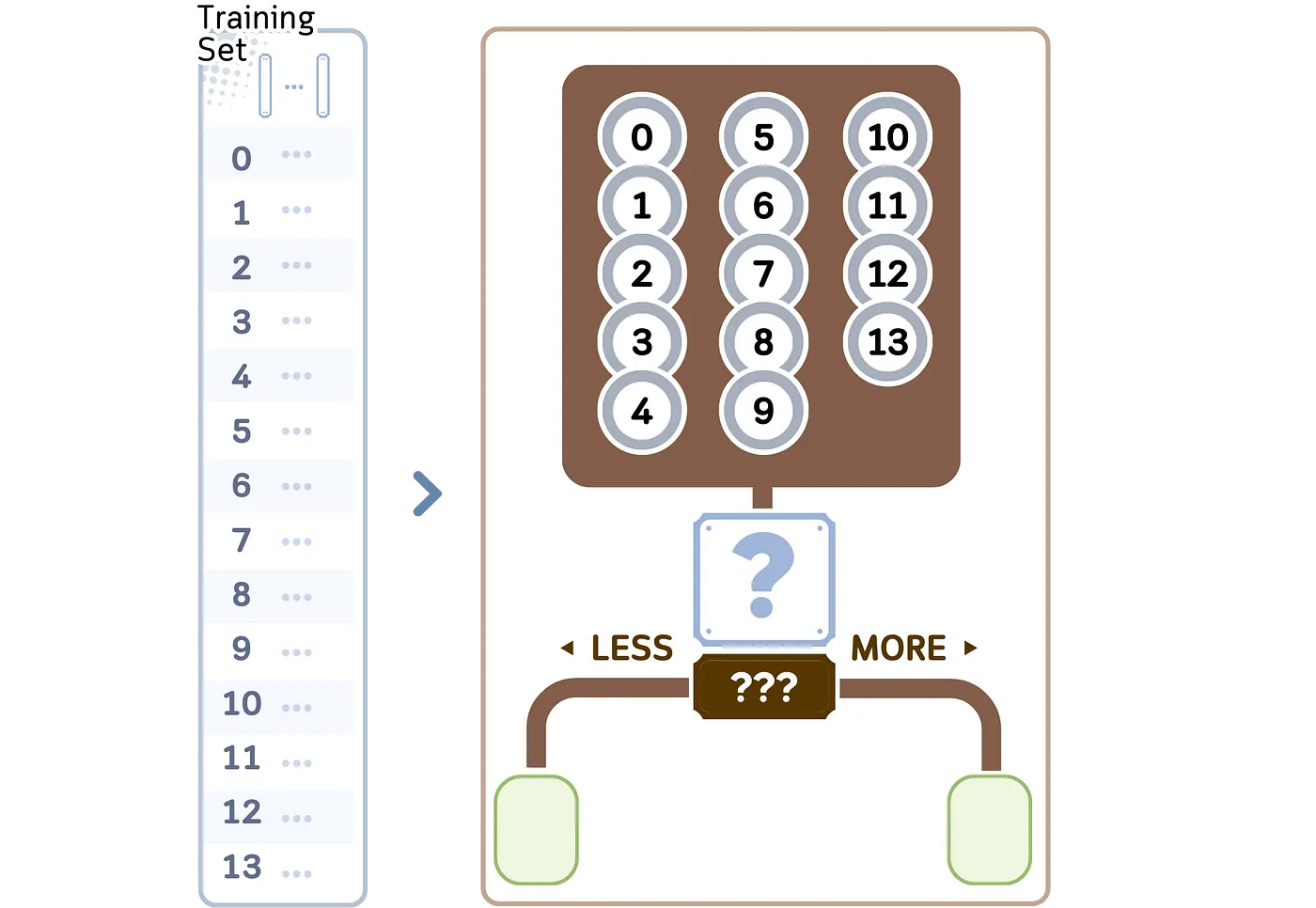
我们将探讨CART(分类和回归树)决策树算法中的回归部分。它构建二叉树结构,通常遵循以下步骤,
1.从根节点的全部训练样本开始。
- 对于数据集中的每个特征来说:
a. 将特征的数值按升序排列。
b. 考虑所有相邻值之间的中点作为可能的分割点。
总共有23个分割点需要检查。
3. 对于每个可能的分割点:
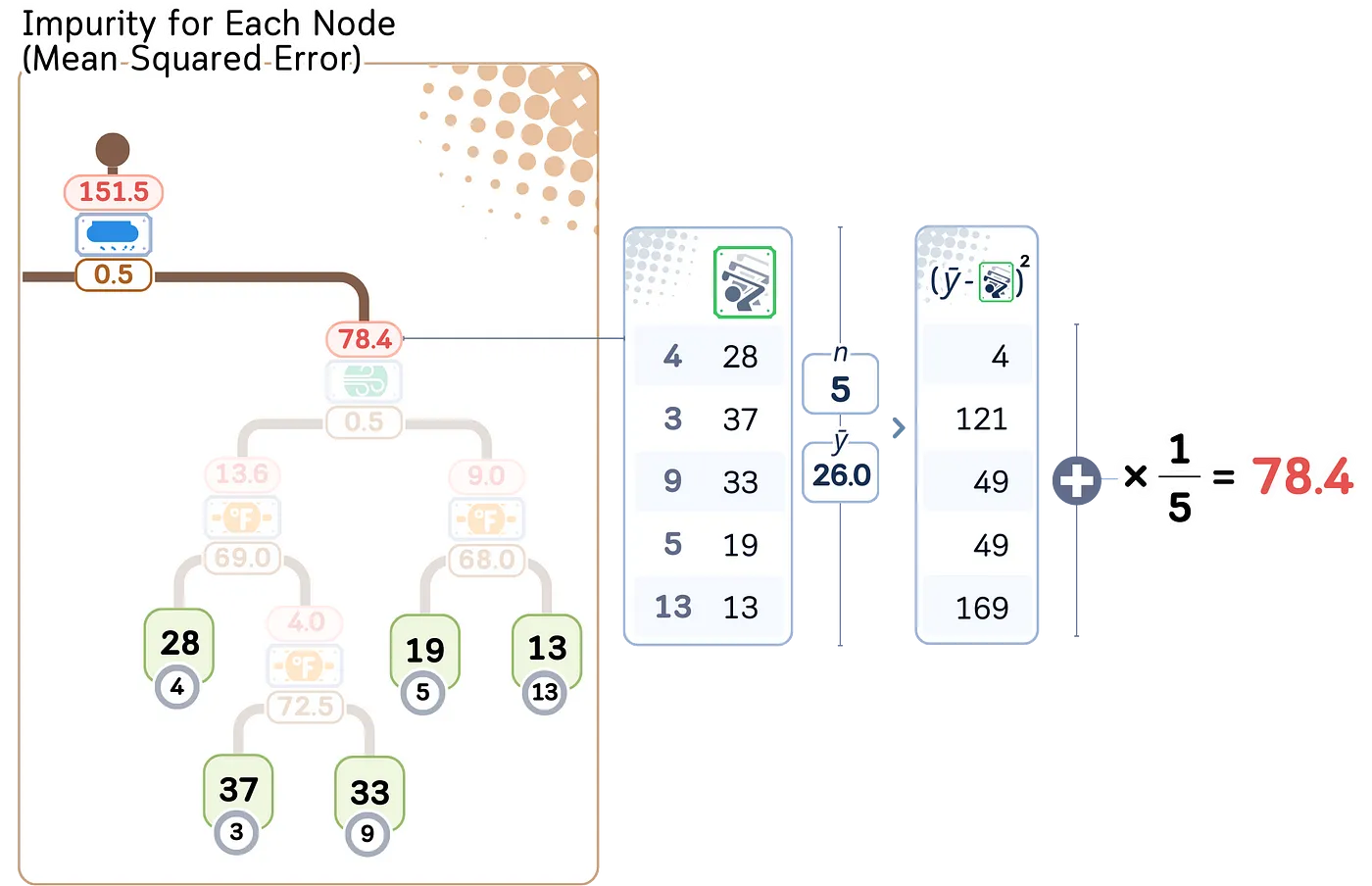
a. 计算当前节点的均方误差(MSE)。
b. 计算分割后的加权平均的预测误差。
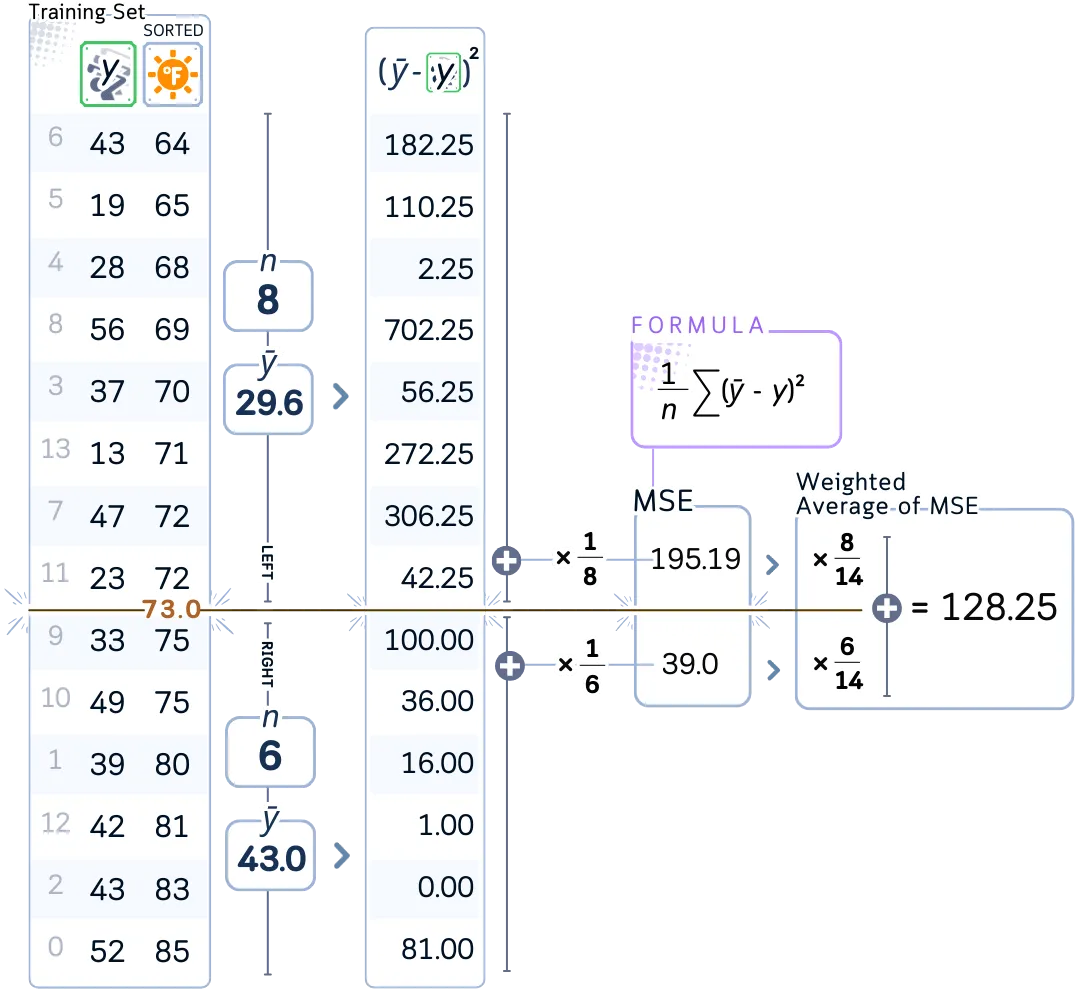
例如,我们计算了温度为73.0的分割点的MSE加权平均。
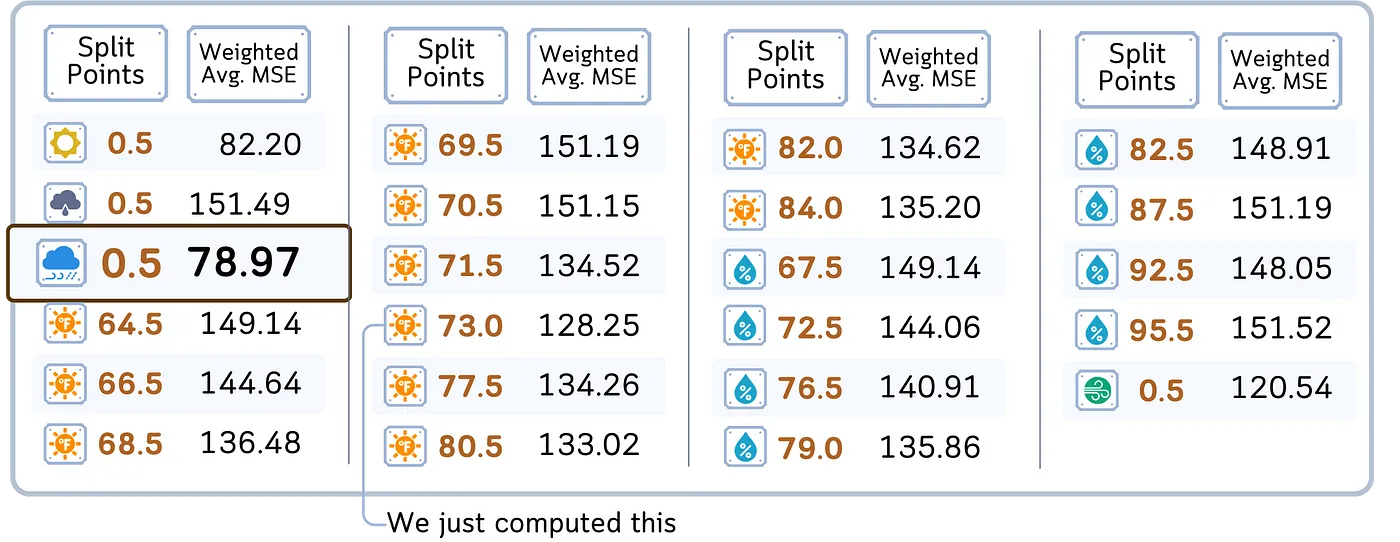
4. 评估完所有特征和分割点后,最后选择加权平均MSE最小的那个特征或分割点。
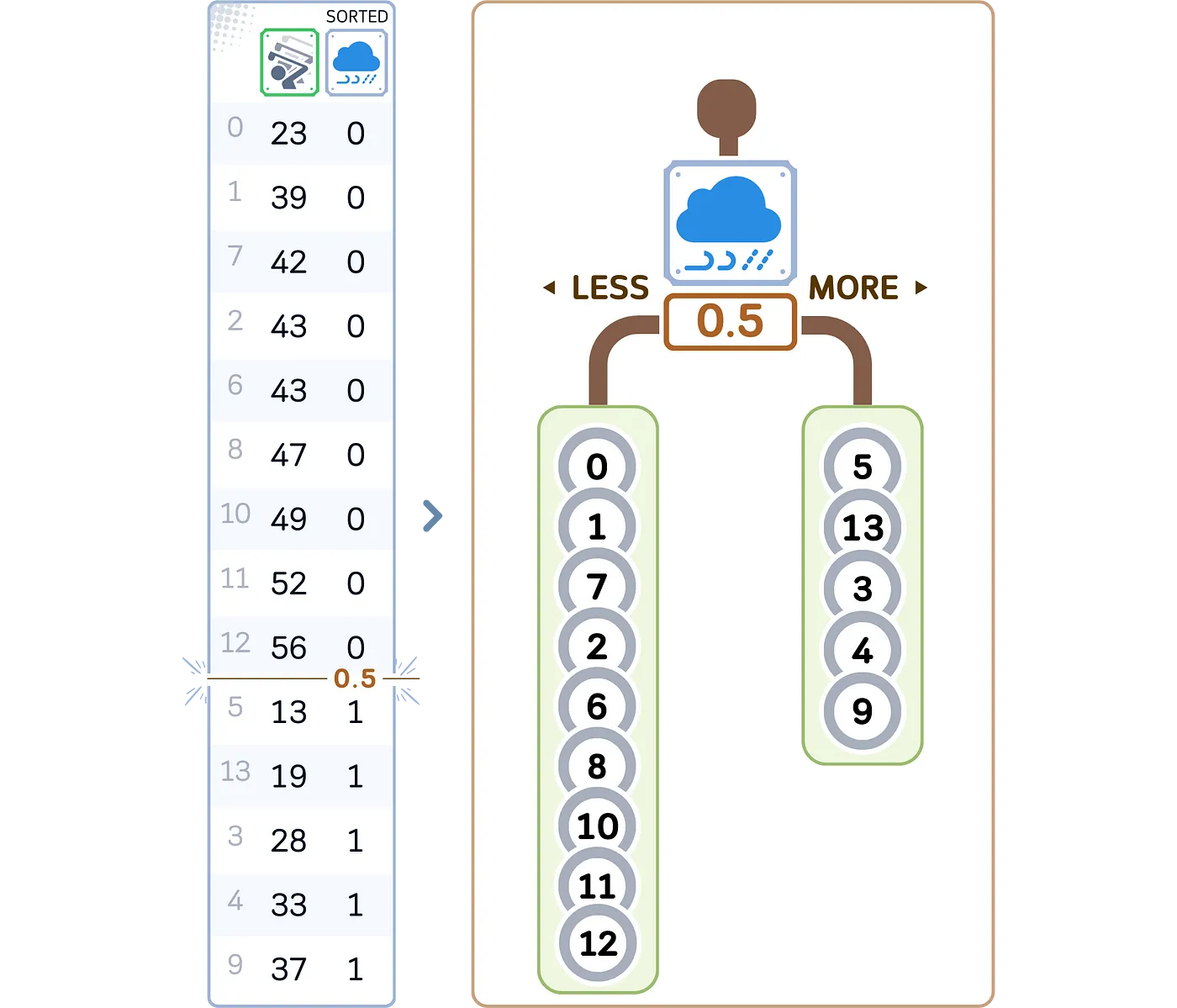
5. 创建两个子节点,根据选定的特征和分割点:
- 左子树:特征值 <= 分割点的样本数据
- 右子树:特征值 > 分割点的样本数据
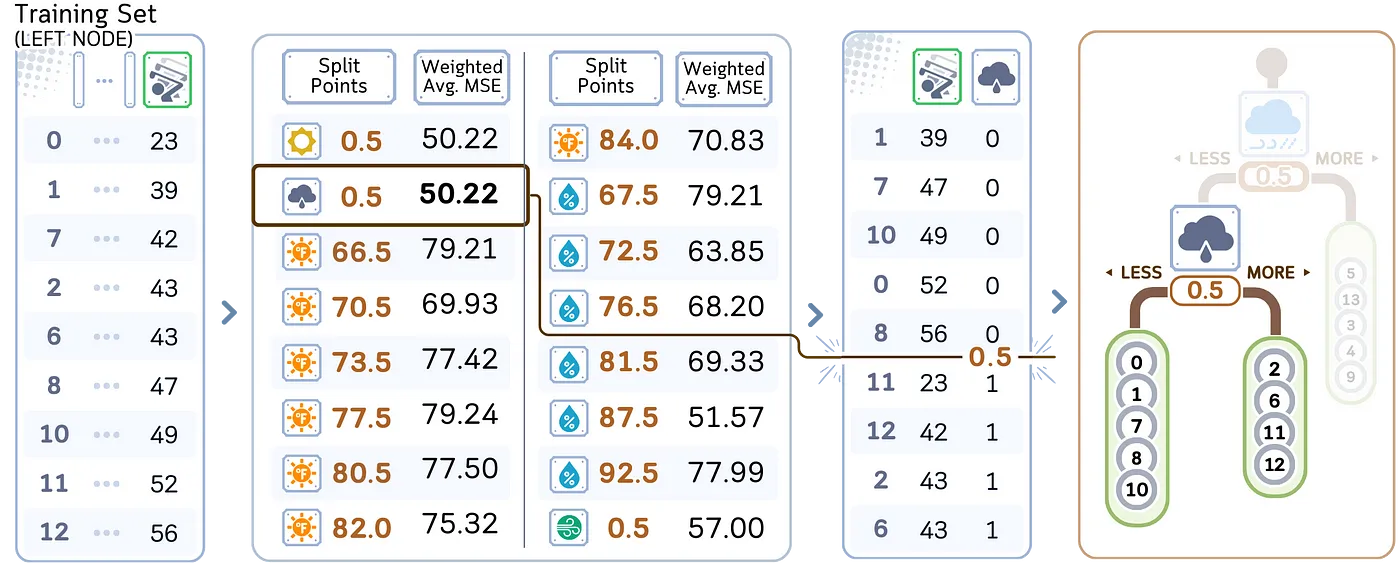
递归地重复对每个子节点执行步骤2–5,直到满足终止条件为止。
- 对于每个叶节点,将该节点的样本平均目标值作为预测。
from sklearn.tree import DecisionTreeRegressor, plot_tree
import matplotlib.pyplot as plt
# 训练模型,如下
regr = DecisionTreeRegressor(random_state=42)
regr.fit(X_train, y_train)
# 可视化决策树
plt.figure(figsize=(26, 8))
plot_tree(regr, feature_names=X.columns, filled=True, rounded=True, impurity=False, fontsize=16, precision=2)
plt.tight_layout() # 调整布局
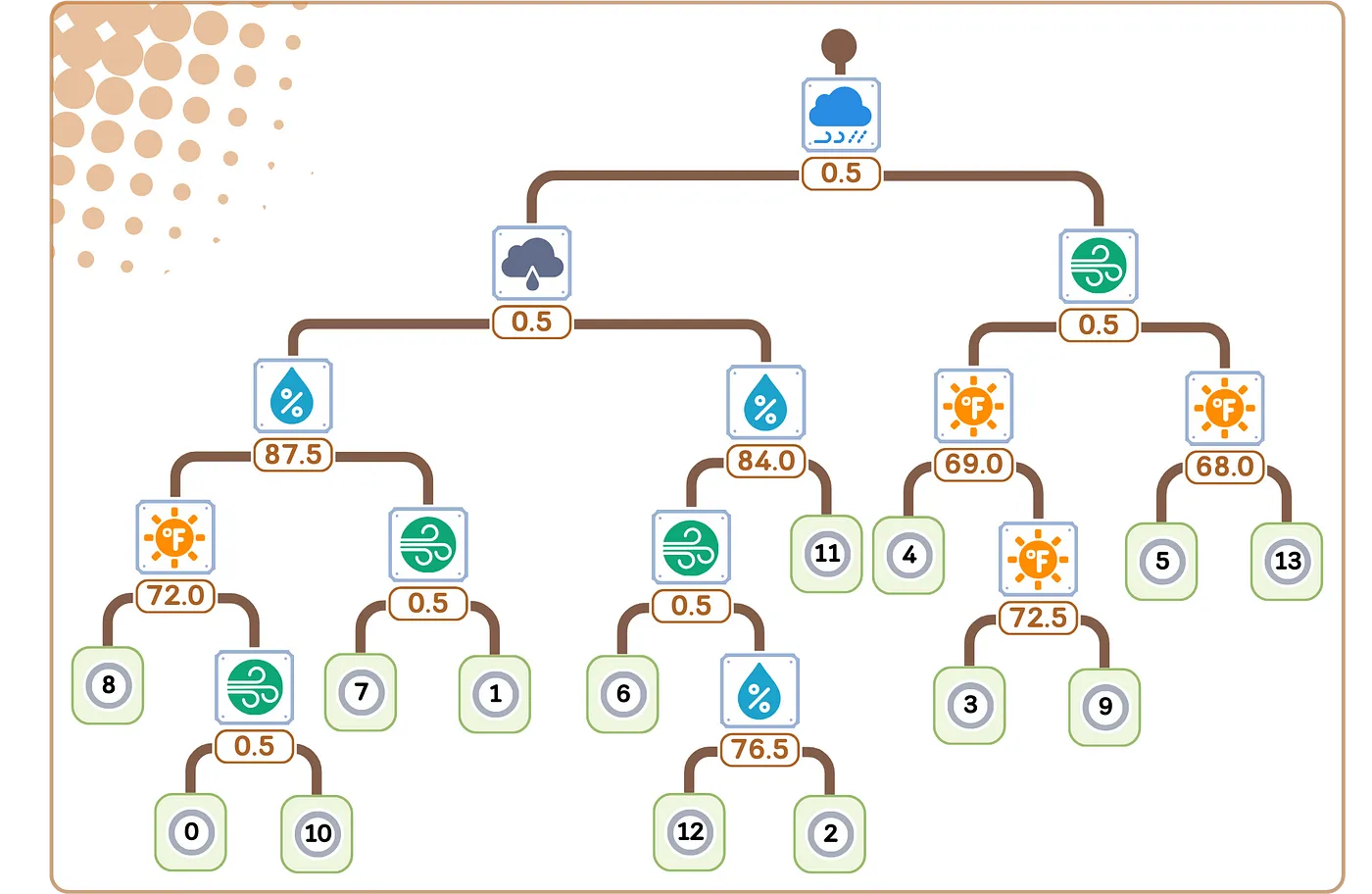
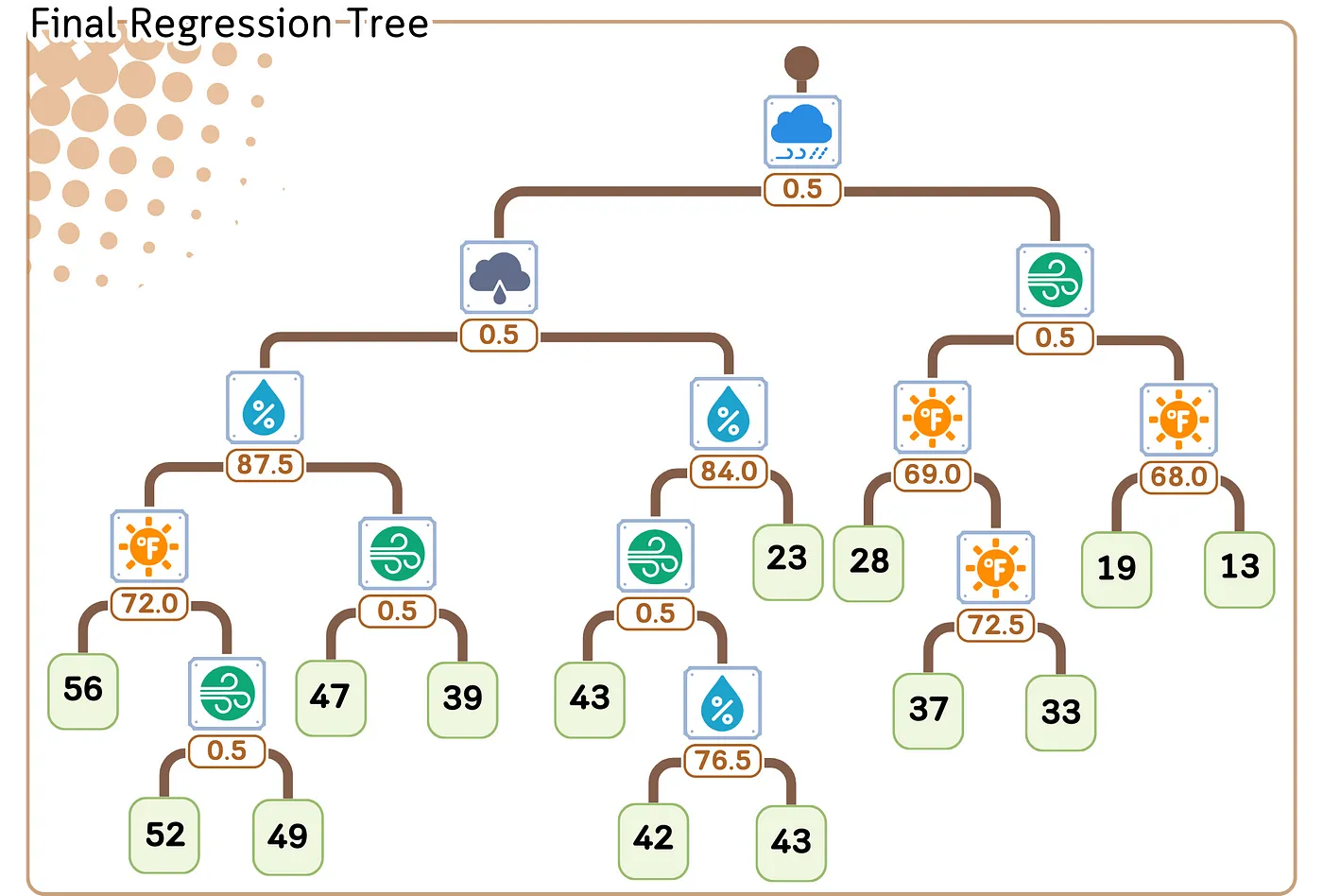
plt.show() # 显示图像在该 scikit-learn 输出中,显示了叶子节点和内部节点的样本及其值。
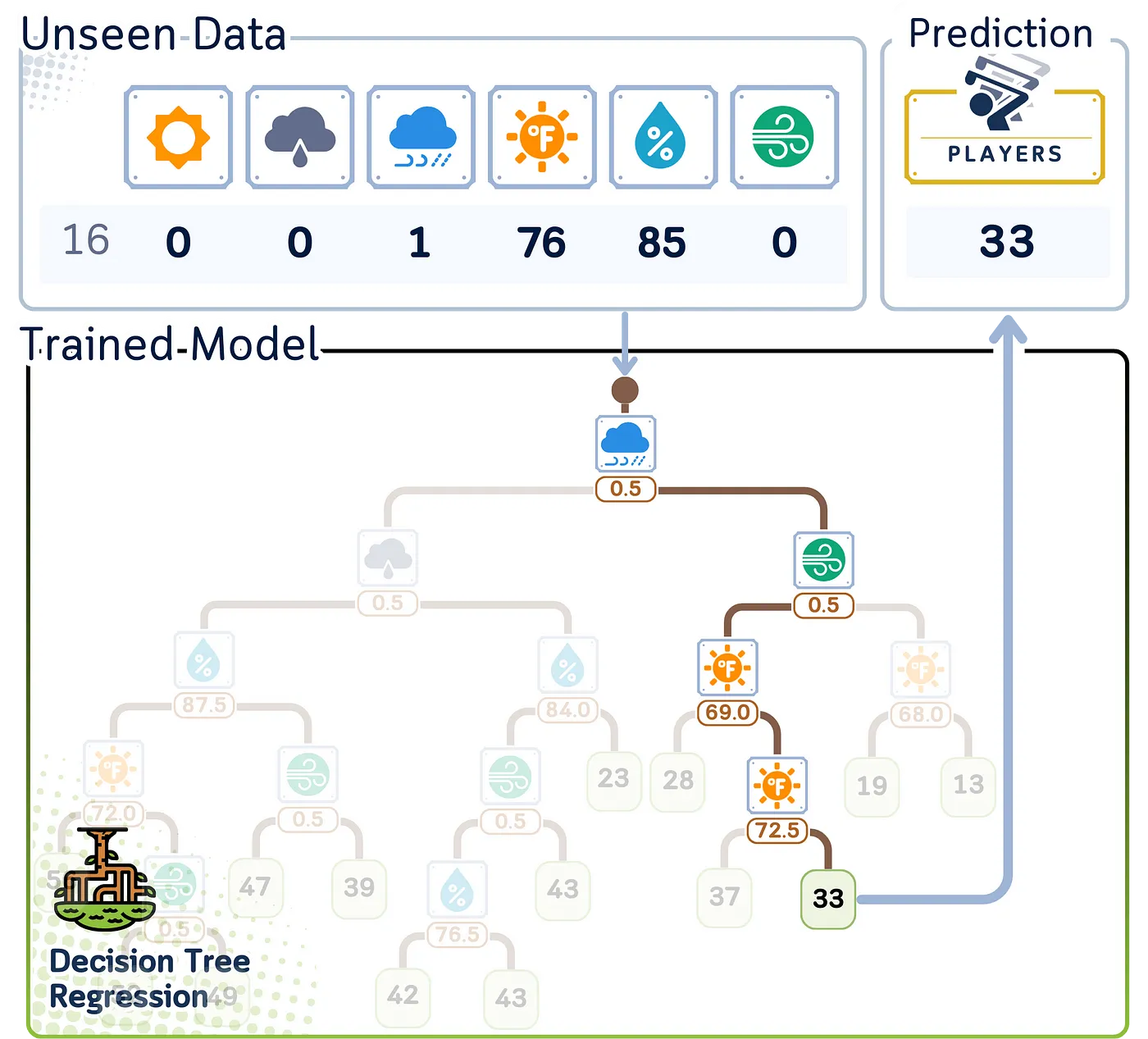
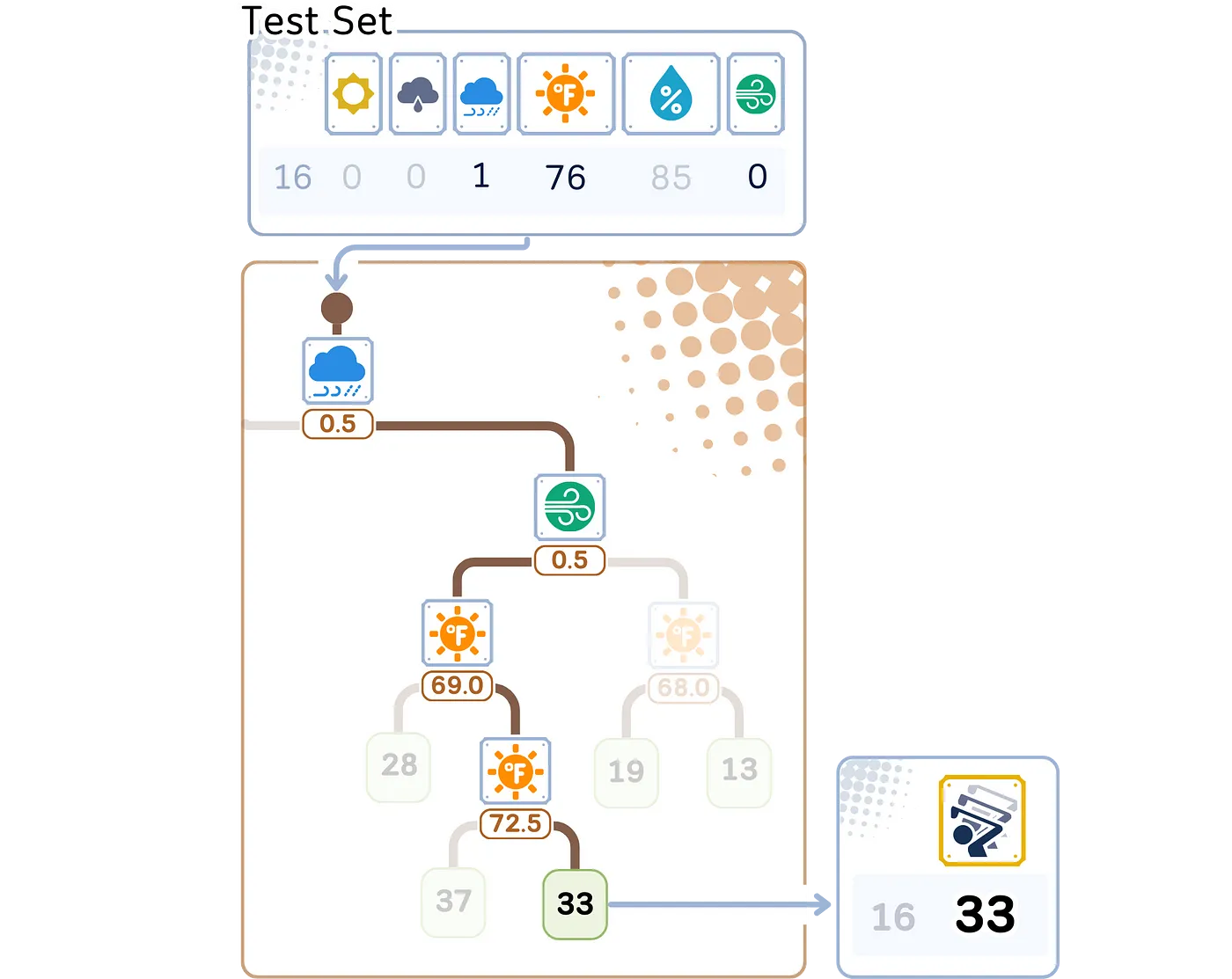
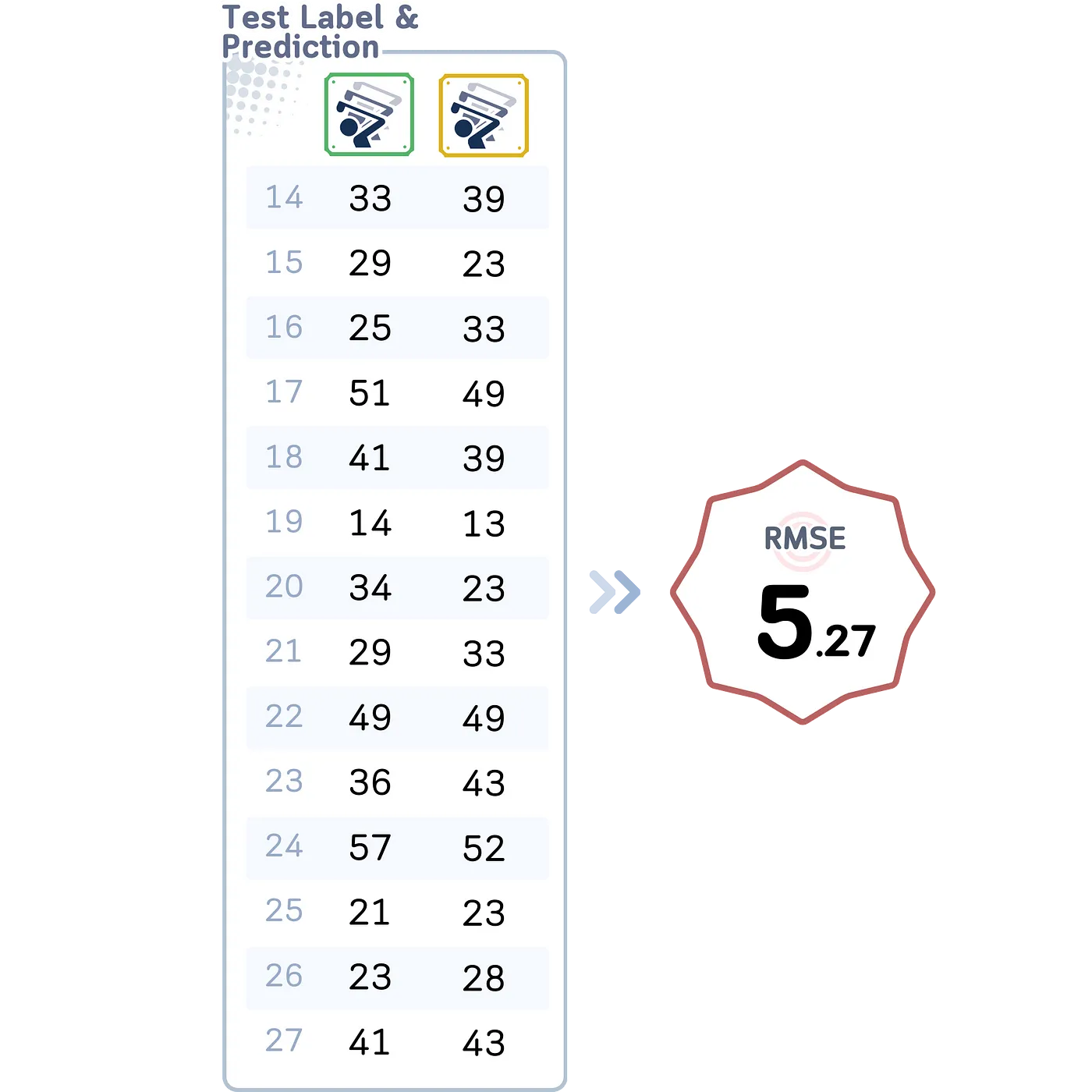
回归预测步骤这里是一个回归树如何对新数据进行预测的步骤:
- 从树的顶部(根)开始。
- 在每个决策点(节点):
- 查看特征和分割值。
- 如果特征值小于或等于分割值,则向左走。
- 如果特征值大于分割值,则向右走。 - 一直向下移动到树的底部,直到到达终点(叶子)。
- 预测结果就是叶子中存储的平均值。
RMSE的值比简单的回归模型的结果好得多。
预剪枝与后剪枝:构建好树之后,我们唯一需要担心的就是如何让树变小以防止过拟合。一般来说,剪枝的方法大致可以分为:
预剪枝预修剪,又称早停,是指根据某些预定义的标准,在训练过程中暂停决策树的增长。这种方法旨在避免树过于复杂并过度拟合训练数据。常用的预修剪方法有:
- 最大深度:限制树可以生长的最大深度。
- 拆分所需的最小样本数:要求每个节点在分裂时必须至少包含一定数量的样本。
- 每个叶子节点的最小样本数:确保每个叶子节点至少包含一定数量的样本。
- 叶子节点的最大数量:限制树中的叶子节点总数。
- 最小不纯度减少:仅允许那些能使不纯度减少到一定量的分裂。
这些方法在满足指定条件时会阻止树的生长,在其构建阶段“剪枝”了树。
这在回归问题中也同样适用。
后剪枝则允许决策树生长到其最大范围,并随后修剪以减少复杂性。这种方法先构建一棵完整的树,然后移除或折叠那些对模型性能贡献不大的分支。一种常见的后剪枝技术称为 代价复杂度剪枝。
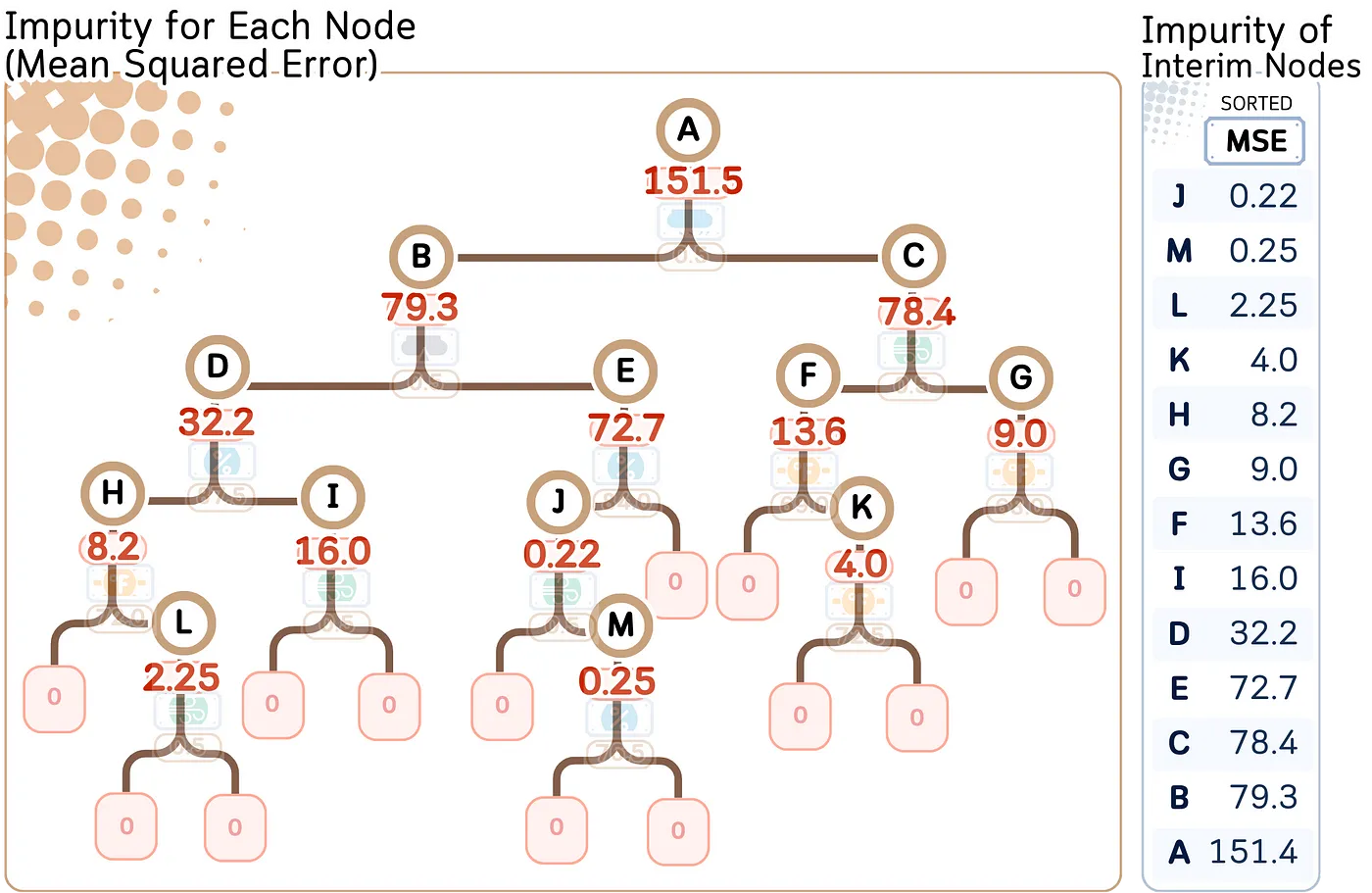
成本复杂度剪枝 计算每个节点的杂质度对于每个中间节点,计算不纯度(在回归情况下,使用均方误差),然后按从小到大的顺序排序。
# 绘制决策树图
plt.figure(figsize=(26,8))
plot_tree(regr, feature_names=X.columns, filled=True, rounded=True, impurity=True, fontsize=16, 精度=2)
plt.tight_layout() # 调整布局,防止元素重叠
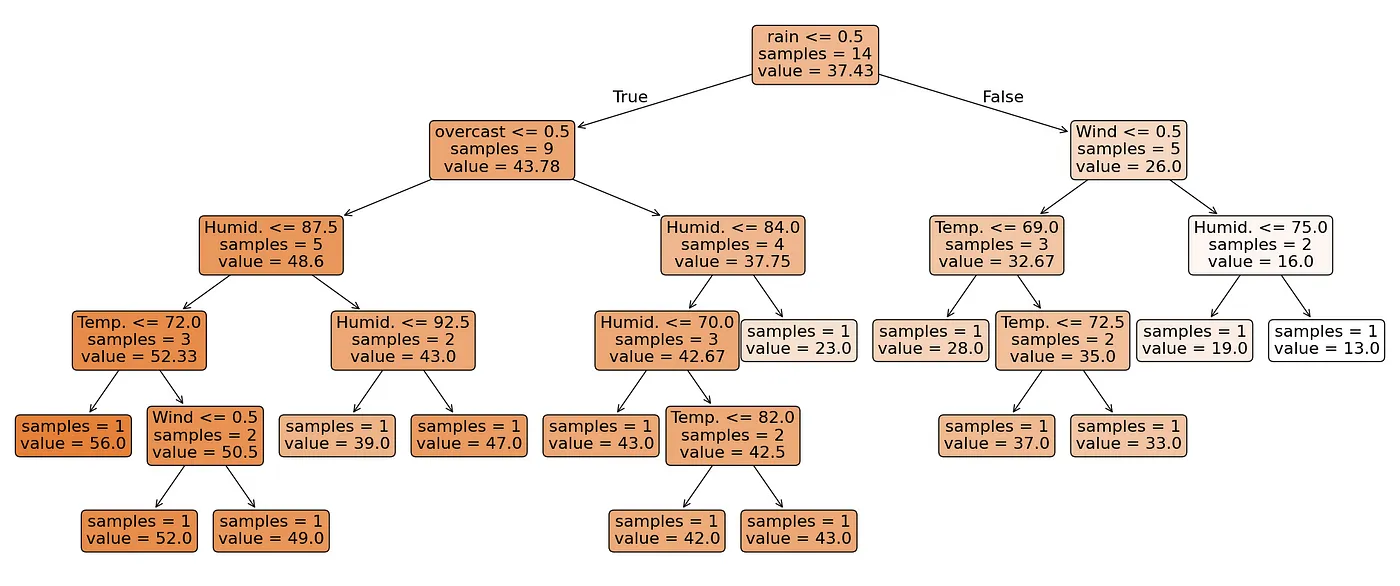
plt.show()在这个 scikit learn 输出中,每个节点的杂质度显示为 “squared_error”。
让我们给这些中间节点(从A到J)命名。然后我们按照它们的MSE值,从低到高排序。
第 2 步:通过去除最弱环节来创建子树目标是逐步将中间节点转化为叶子,从MSE最低的节点(=最弱环节)开始。我们可以根据这个原则创建一条修剪路径。
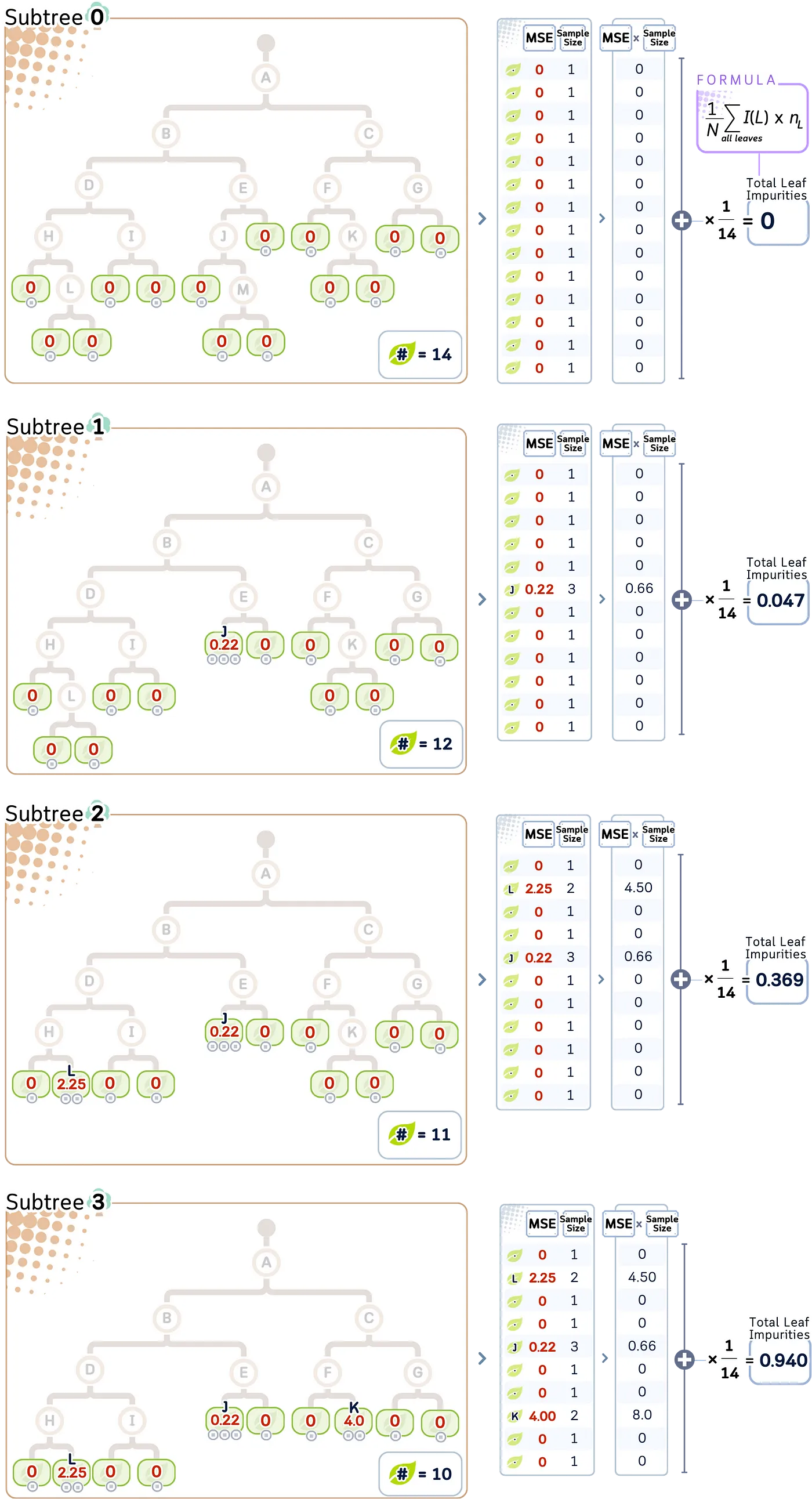
我们将它们命名为“子树 i”,其中 i 表示修剪的次数。从原始树出发,树将在具有最低MSE的节点开始修剪(从节点J开始,J剪除了M,接着是L,K等)。
第三步:计算每个子树的总叶杂质量对于每个子树 T,总叶杂质 _R(T) 可以计算为:
R(T) = (1/N) Σ I(L) * n _L
其中 R 表示... T 表示... N 表示... I 表示... L 表示... n 表示...
where:
· L 表示所有叶节点
· _nL 表示叶节点 L 中的样本数
_· N 表示树中的总样本数
· I(L) 表示叶节点 L 的不纯度(MSE)
我们修剪得越厉害,叶片的杂质就越多。
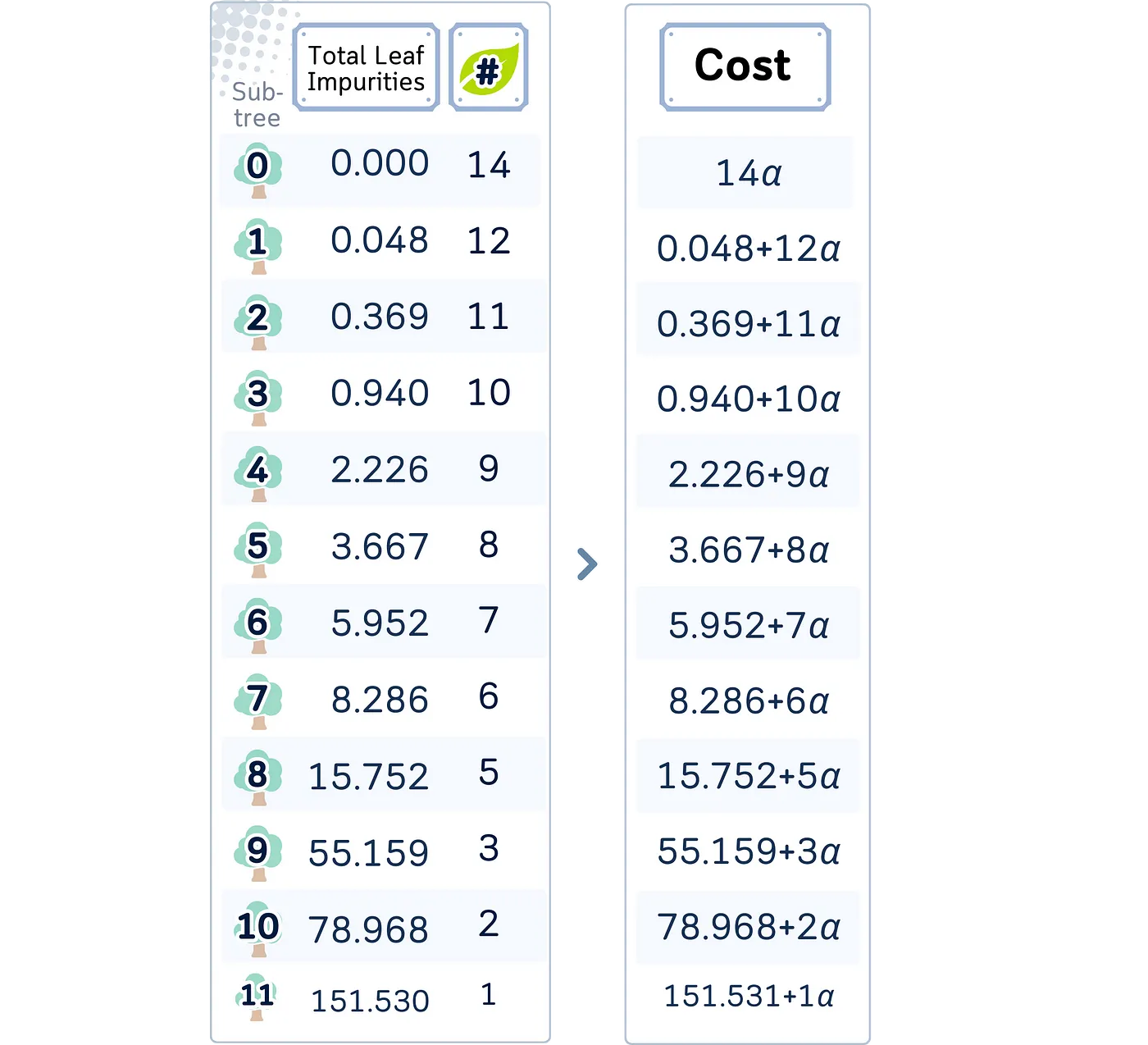
步骤 4:计算成本公式
为了控制何时停止将中间节点转换为叶子节点,我们首先使用以下公式来评估每个子树_T_的成本复杂性:
成本(T) = R(T) + α * |T|
在哪里:
· R(T) 是总叶节点杂质
· |T| 是子树 T 中叶节点的数量
· α 是复杂度参数
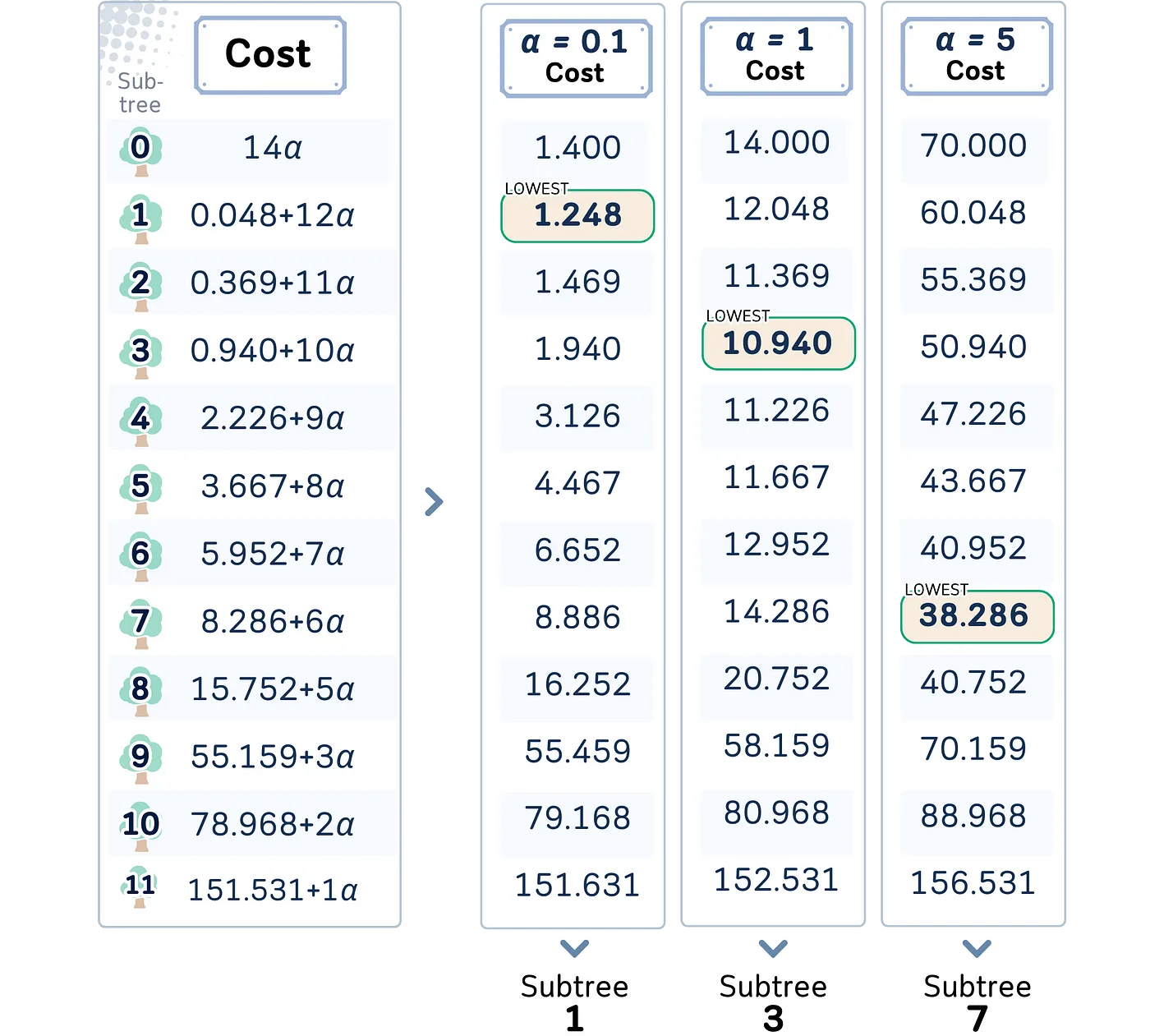
alpha的值决定了我们将选择哪个子树。成本最低的子树将会成为最终的树。
当 α 较小时,我们更关注准确度(也就是更大的树)。当 α 较大时,我们更倾向于简单性(也就是更小的树)。
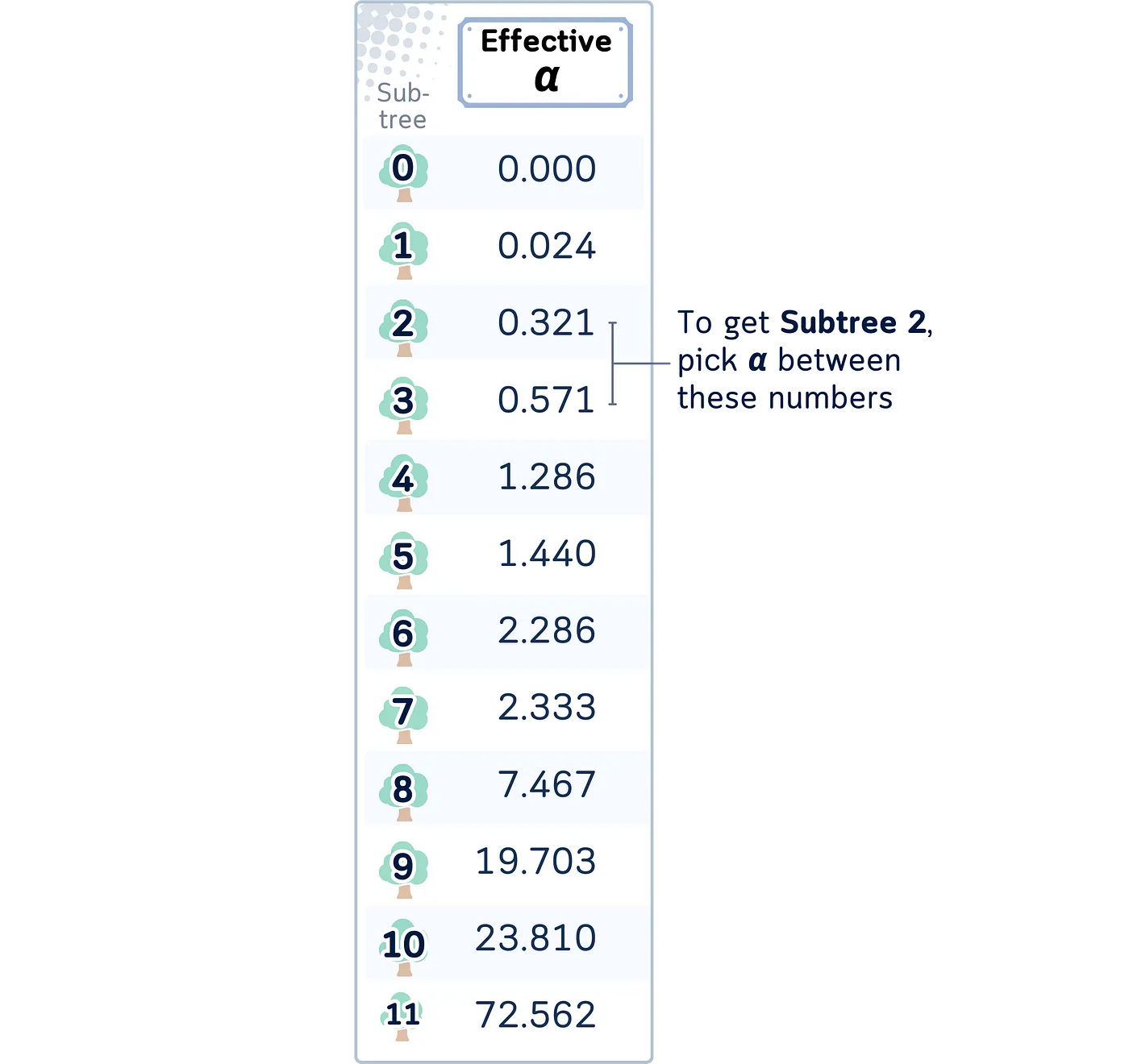
虽然我们可以自由设置 α ,在 scikit-learn 中,你也可以得到特定子树的最小的 α 。这被称为 有效 α。
这个有效的 α 也可以计算出来。
# 计算成本复杂度剪枝路径
tree = DecisionTreeRegressor(random_state=42)
effective_alphas = tree.cost_complexity_pruning_path(X_train, y_train).ccp_alphas
impurities = tree.cost_complexity_pruning_path(X_train, y_train).impurities
# 定义一个计算叶子节点个数的函数
count_leaves = lambda tree: sum(tree.tree_.children_left[i] == tree.tree_.children_right[i] == -1 for i in range(tree.tree_.node_count))
# 针对每个复杂度参数训练树并计算叶子节点的数量
leaf_counts = [count_leaves(DecisionTreeRegressor(random_state=0, ccp_alpha=alpha).fit(X_train_scaled, y_train)) for alpha in effective_alphas]
# 创建一个包含分析结果的数据框
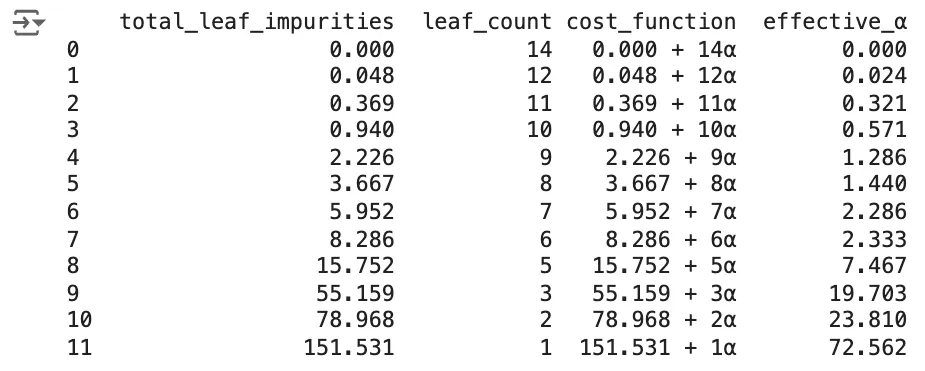
pruning_analysis = pd.DataFrame({
'total_leaf_impurities': impurities,
'leaf_count': leaf_counts,
'cost_function': [f"{imp:.3f} + {leaves}α" for imp, leaves in zip(impurities, leaf_counts)],
'effective_α': effective_alphas
})
print(pruning_analysis)预先修剪的方法通常更快且占用内存更少,因为它们从一开始就防止树长得很庞大。
后剪枝技术可以通过评估整个树再做剪枝决定,从而有可能创建更优化的树。因为它会评估整个树的结构再进行剪枝决定。然而,它可能需要更多的计算资源。
创建一个能够很好地泛化到未见数据的模型是目标,而选择何时进行预剪枝或后剪枝,或者两者结合,通常取决于特定的数据集、当前的问题,当然还包括可用的计算资源。
实际上,通常会同时使用这些方法,比如应用一些预剪枝的标准来防止生成出过大的树,然后再使用后剪枝技术来微调模型的复杂性。
🌟 决策树回归模型(带代价复杂度剪枝)代码概览 import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
from sklearn.tree import DecisionTreeRegressor
from sklearn.preprocessing import StandardScaler
# 创建数据集
dataset_dict = {
'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
'Num_Players': [52,39,43,37,28,19,43,47,56,33,49,23,42,13,33,29,25,51,41,14,34,29,49,36,57,21,23,41]
}
df = pd.DataFrame(dataset_dict)
# 对 'Outlook' 列进行独热编码
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
# 将 'Wind' 列转换为二进制
df['Wind'] = df['Wind'].astype(int)
# 将数据划分成特征和目标,然后划分成训练集和测试集
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# 设置决策树回归器
tree = DecisionTreeRegressor(random_state=42)
# 计算成本复杂度路径、不纯度和有效 alpha
path = tree.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities
print(ccp_alphas)
print(impurities)
# 使用选定的 alpha 值训练最终决策树
final_tree = DecisionTreeRegressor(random_state=42, ccp_alpha=0.1)
final_tree.fit(X_train, y_train)
# 预测
y_pred = final_tree.predict(X_test)
# 计算并输出 RMSE
rmse = root_mean_squared_error(y_test, y_pred)
print(f"RMSE: {rmse:.4f}")要详细了解Decision Tree Regressor、Cost Complexity Pruning及其在scikit-learn中的实现,读者可以参考它们的官方文档。这些文档提供了关于如何使用它们和调整参数的全面信息。
技术环境:本文使用了 Python 3.7 和 scikit-learn 1.5。虽然文中讨论的概念通常是通用的,但具体代码实现可能因版本不同而有些许不同。
关于这些插图:除非特别注明,所有图片均由作者制作,包含来自Canva Pro的授权设计元素。
共同学习,写下你的评论
评论加载中...
作者其他优质文章