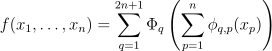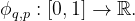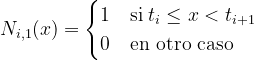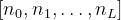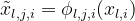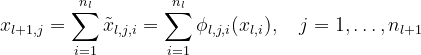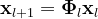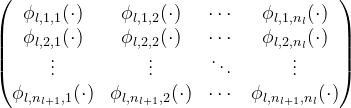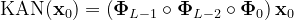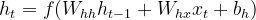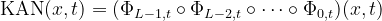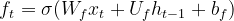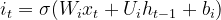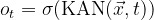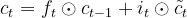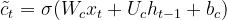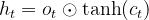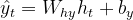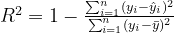探索非线性动力学与机器学习在时序数据处理中的交叉点
在一个日益依赖数据的世界里,精确预测未来事件的能力变得越来越重要,是科学进步和技术创新的基石。从预测金融市场走势到预测气候模式,准确的预测帮助决策者有效制定策略,降低风险,抓住机会。
时间序列预测法,一种根据过去观察到的值来预测未来值的科学,在各个领域都至关重要,不可或缺。尽管已经取得了显著的进步,但由于时间数据本身固有的复杂性——非线性、长期依赖性以及随机性——预测依旧是一项艰巨的任务。
股票指数可以被视为时间序列,资产价格随时间变化,由于这些序列具有很高的随机性,预测起来非常复杂。
本文开始进行数学探索,探讨时间 Kolmogorov–Arnold 网络(TKAN),这是一种新颖的神经网络架构,为时间序列预测提供了另一种方法。我们将深入探讨其理论基础和架构,剖析其复杂的架构,并与传统的循环神经网络(RNN)进行性能比较。
这里是可以配套的笔记本链接。here is the link to the companion notebook. 在LinkedIn上与我联系here。让我们开始!
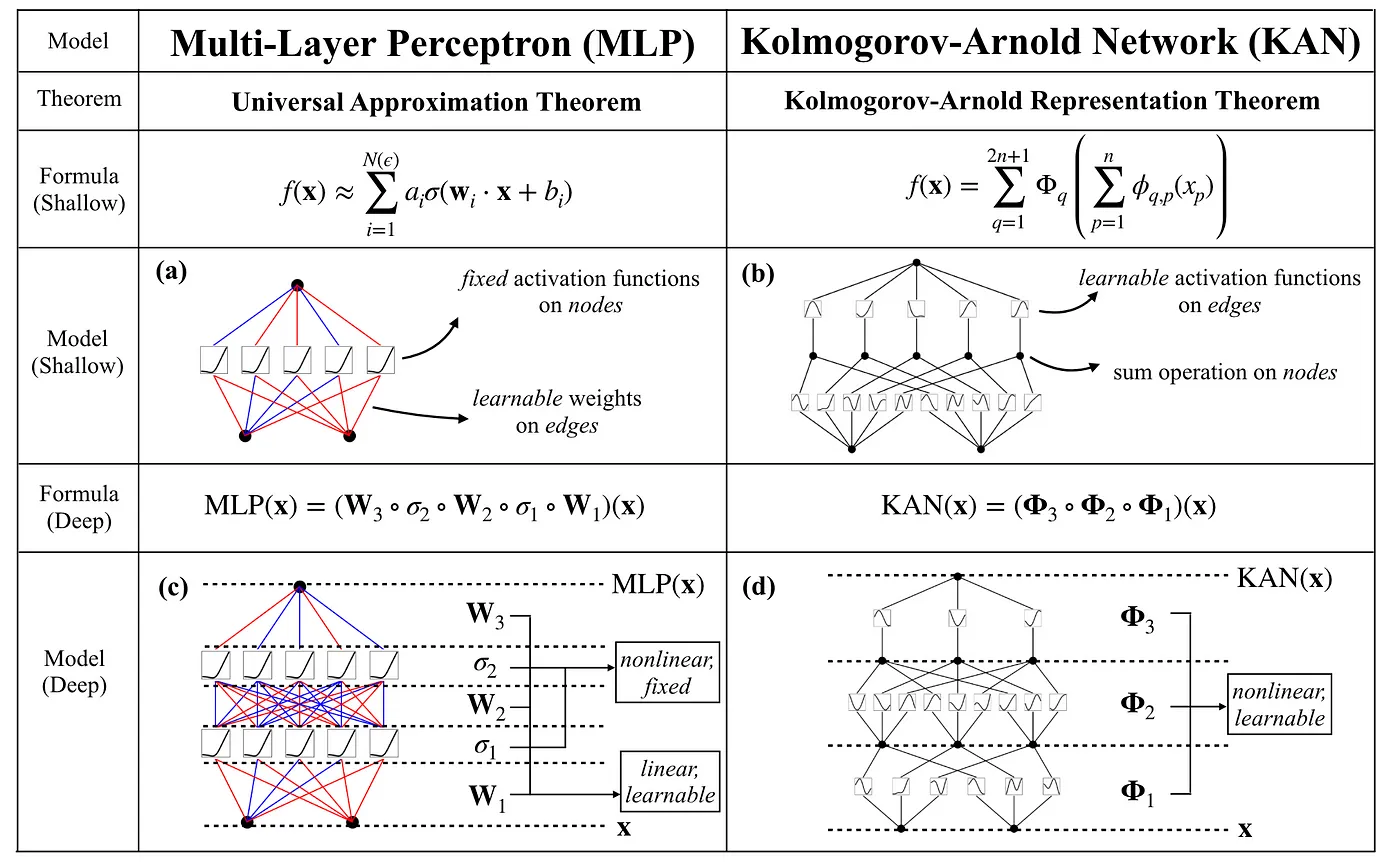
通用近似定理与多层感知器 (MLPs)注:MLPs即多层感知器,是一种常用的神经网络模型。在神经网络的世界里,多层感知机(MLPs)一直是近似复杂函数的基础模型。这一模型源于罗森布拉特在1958年提出的感知机,通过增加隐藏层,多层感知机能够近似任何连续函数——这一概念由通用近似定理正式确立。然而,有一个强大的定理提供了函数近似的不同视角:柯尔莫哥洛夫-阿诺尔德表示定理。这一定理为柯尔莫哥洛夫-阿诺尔德网络(KAN)奠定了基础,我们将在本文中探讨这种架构。
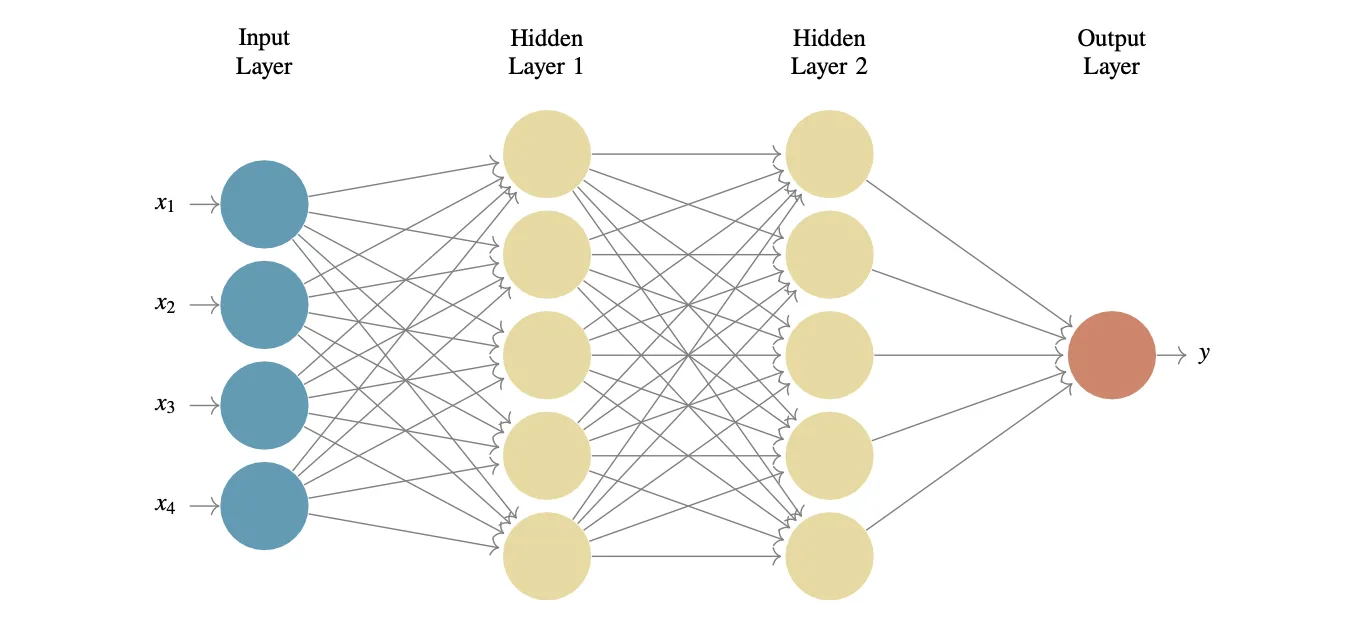
具有2个隐藏层的前馈神经网络。
在开始讨论KANs之前,我们先简要回顾一下多层感知器(MLP,即多层感知机)和通用近似定理。MLP是一种前馈神经网络(FFNN),它包括输入层、一个或多个隐藏层和输出层。每一层都包含神经元,这些神经元进行线性变换,然后应用非线性激活函数。
通用逼近定理表明,具有有限数量神经元的单隐藏层前馈神经网络(FFNN),在适当选择激活函数和权重的情况下,可以逼近任何在 $R^n$ 的紧子集上的连续函数。值得注意的是,这个定理突显了多层感知器(MLPs)在函数逼近任务中的强大功能。
科尔莫戈罗夫-阿诺德网络(KAN):KAN网络,也就是基于Kolmogorov-Arnold表示定理(KARD)的网络,该定理说明,任何多变量的连续函数都可以通过单变量函数和加法操作来表示。这一定理对KAN网络至关重要,因为它说明理论上来说,任何多变量函数都能被拆解成一系列单变量函数。
柯尔莫哥洛夫-阿诺尔德(柯-阿)表述定理可以表述为如下:
如下
- ϕ_q,p 是单变量函数,将每个输入变量x_p 属于 [0,1] 区间的每个输入变量映射到实数集 R。
- Φ_q 是一个将这些一元函数的和作为输入的一元函数。
基本上,这个定理表明我们可以将任何复杂的函数分解成更简单的函数的和与复合,这对于设计KAN网络来说非常重要。这使得在神经网络中学习复杂函数变得更加简单。
关于MLP神经网络这一块:
这些单变量函数 _ϕq,p 类似于我们在神经网络层中看到的非线性变换,而函数 _Φq 表示这些变换的合成。然后,就像在多层感知器(MLP)网络中一样,我们可以通过增加更多的层来使KAN变得更加复杂。
一元函数的参数化由于柯尔莫哥洛夫-阿诺德表示法中的所有函数都是一元的,我们可以将每个函数表示为一个 B样条曲线。B样条是分段多项式函数,可以灵活地用来描述曲线。通过调整局部B样条基函数的系数,我们可以在训练过程中学习这些一元函数的特性。
:
- _cq,p,i 是与基函数关联的可调整系数。
- _Ni,k (x) 是 k 阶的B样条基。
- k 是样条阶数。
当 k = 1 时,B样条基函数可以定义为
当 k > 1 时,通过 Cox-de Boor 递归公式,我们就可以得到
通过这种方式,通过将这些函数表示为B样条或B-spline,我们可以。(根据目标读者的专业背景选择术语)
- 通过在训练过程中调整B样条的系数来学习复杂的非线性函数:
- 通过确保所学函数保持平滑和连续性,这对于在KAN中逼近连续函数至关重要:
- 得益于B样条的特性,参数优化更加稳定和高效:
KAN中的一个层级可以这样定义,如下所示:
这里,n(in)_ 是输入变量的数量,n(out)_ 是输出变量的数量。具体来说,Kolmogorov-Arnold 定理有 n(in) = n_,和 n(out) = 2n+1.
简而言之,每个KAN网络层都有可以在网络训练过程中调整的参数化函数。这就是KAN网络如此强大的原因之一,因为要学习的函数是一元的,这使得它们处理起来更简单,比一般的多维函数更易于处理。
KAN网络计算我们表示KAN的形状为
其中,_ni 表示第 i 层中的神经元数量,而 L 是总层数。设 (l, i) 表示第 l 层中的第 i 个神经元,这里所说的 激活值 指的是神经元的输出值,神经元 (l, i) 的 激活值 通常用 x(l,i) 表示。
每个函数 ϕ(l,j,i) 连接神经元 (l,i) 到神经元 (l+1,j),_ 函数 ϕ(l,j,i) 的 预激活 是 x(l,i),_ 而 后激活 则是:。
神经元 (l+1,j) 的激活值是所有传入后激活值的总和。
我们可以用矩阵形式来表达前向传播:
其中 _xl 是第 l 层的激活值向量,_Φl 则是该层的函数权重矩阵。
最后,一个通用的KAN网络由多个层次构成。如果总共有L个层次,我们可以用以下方式表示输入_𝑥0的KAN网络的最终结果:
即,网络的输出结果是通过依次将每个层 _Φl 应用到前一层的输出上来获得的,这与传统的深度神经网络的工作方式相似。
关于多层感知器(MLP)和KAN网络之间差异的总结,摘自刘, Z., 王, Y., 维迪亚, S., 鲁尔, F., 霍尔夫森, J., 施洛贾西奇, M., 侯, T. Y., & 特格马克, M. (2024). KAN: Kolmogorov-Arnold Networks. arXiv. https://arxiv.org/abs/2404.19756。
总之,KAN网络从Kolmogorov-Arnold表示法中获得灵感,通过组合一元函数来表示复杂的多元函数。这为传统的神经网络带来了不同的视角,并开启了对复杂函数进行更深层和更高效表示的大门,同时保持学习在可以管理的一元空间内。
这种方法不仅能让复杂的函数学习变得更简单,还能加深函数理论与现代神经网络设计之间的联系。
时序Kolmogorov-Arnold网络(TKAN)TKAN(时间序列KANs) 是对柯尔莫哥洛夫-阿诺尔德网络(KANs)的扩展,专门设计来处理序列数据或时间序列。它们结合了循环网络(RNNs)和长短期记忆(LSTMs)网络的优点,能够捕捉时间依赖性,并处理随时间演变的数据序列。
TKAN背后的关键理念是结合KAN学习复杂函数的能力与LSTMs保持对过去事件的长期记忆的能力,使它们成为时间序列预测任务中的强大工具。
TKAN的主要组成部分:- RKAN 层: 帮助网络保留先前状态的短期记忆。每个 RKAN 层在处理过程中管理这些记忆。
- 门控机制(类似 LSTM): 有助于管理信息流动。模型决定保留或遗忘哪些信息。
注:TKAN为特定术语,此处保持原样。
1. 递归柯尔莫哥洛夫-阿诺尔德网络(RKAN):
当我们与时间序列和循环神经网络(RNN)打交道时,我们会引入时间因素𝑡到变换中。用𝜏=1,2,...来标记离散的时间步。每个时间步都有前向传播和反向传播。在前向传播过程中,计算每个单位的输出或激活值。在反向传播过程中,计算所有权重的误差值。在每个时间步中,RNN处理当前输入 _𝑥t 和来自前一步的隐藏状态 h(t-1)_。
RNN中的隐藏状态 _h__ t 更新方式如下。
其中:
- _ht 是时间步 𝑡 的隐藏状态。
- 递归权重矩阵 𝑊_(ℎℎ) 将前一时间步的隐藏状态 h(t-1_) 进行转换。
- 输入权重矩阵 𝑊_(ℎ𝑥) 将当前输入 _𝑥t. 进行转换。
- 𝑏_ℎ 是偏置向量。
- 非线性激活函数 𝑓(⋅)
这种隐藏的状态更新让网络可以通过数据流捕捉短暂的信息。
在RKANs中,提出了一种新的更新方法来保持过去条目的记忆。将转换函数𝜙_(l,j,i)重新定义为时间相关。这样,层𝑙+1中的节点𝑗在下一个时间步长的激活值如下所示:
这里,__hl,i 是一个记录第 l 层节点 i 历史的记忆函数。
这里 W(hh)_ 和 W(hz)_ 是权重矩阵,分别用来衡量过去值和最近输入的权重。现在KAN网络的每一层都加入了记忆管理功能。
每个 Φ(l,t)_ 是层 l 在时间 t 的函数矩阵 Φ(l,t)_。
2. 将RKAN层与LSTM记忆功能结合起来:
TKANs结合了RKAN层和LSTM记忆机制。LSTM的一个基本组成部分是用于控制信息流动的门控机制。这些门让网络能够决定随着时间推移应该保留哪些信息,舍弃哪些信息。
- 遗忘闸 _ft : 决定丢弃先前状态中的哪些信息:
其中 σ 是 sigmoid 函数,_Wf 、_Uf 和 _bf 是网络的参数。
输入门 _it : 控制要加入哪些新信息到现在的状态中:
输出门 _ot : 决定在当前时刻应该输出哪些信息。
隐藏状态 _ht 根据记忆单元 _ct 更新。
其中 ⊙ 表示逐元素乘法,该表达式表示的是内部状态:
最后,隐状态更新为:
最终的预测是通过一个线性层计算出来的:
此处:
- W 是在预测中用于转换隐藏状态 _ht 的权重矩阵。
- _by 偏置向量。
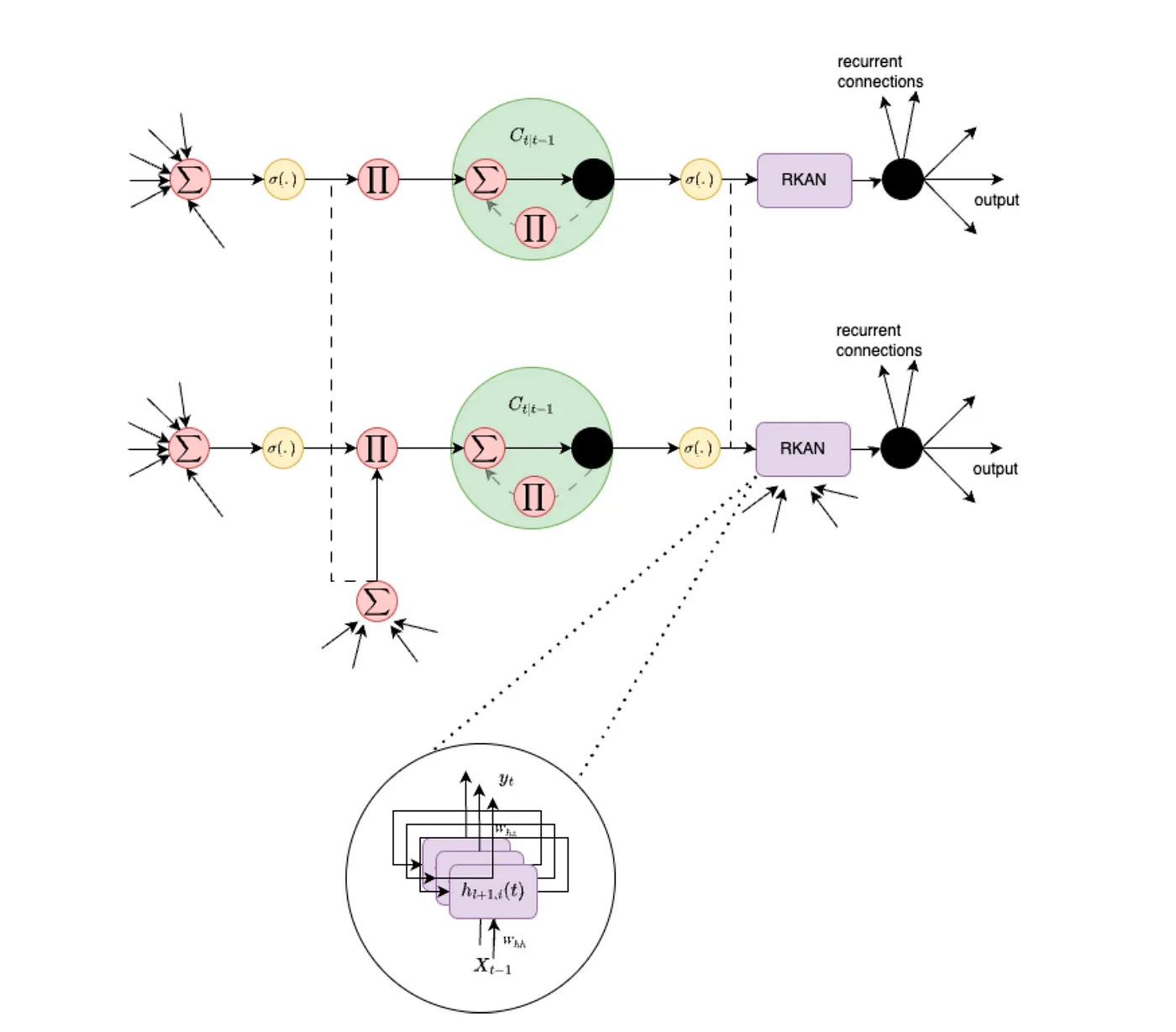
来自 Genet, R. 和 Inzirillo, H. (2024) 的文章 TKAN: Temporal Kolmogorov-Arnold Networks. arXiv. https://arxiv.org/abs/2405.07344 中的一个两层 Temporal Kolmogorov-Arnold 网络 (TKAN) 块。
时空科莫格洛夫-阿诺尔德网络(TKANs) 表示 RKANs 学习复杂函数和 LSTMs 处理长期时间依赖性的强大能力。通过在每一层整合记忆机制,TKANs 能够有效执行序列预测任务,同时处理数据流中的非线性及时间动态。
这种方法是创新的,为多步时间序列预报提供了一个稳健的框架,用于克服传统RNNs的局限,并将KANs在时域中的潜力进一步发挥。
应用和成果时间序列预测分析是许多金融和经济领域中的一个关键任务,在这些领域中,预测诸如股票价格或股市指数表现的未来行为的能力至关重要。标普500指数,反映美国前500家上市公司的表现,是评估金融市场健康状况的关键指标之一。
多步预测法 是一种试图预测时间序列的几个未来步骤的方法,这比单变量(“单步”)预测更复杂。这是因为随着预测时间跨度的增加,不确定性往往会增加。在这个项目中,我们对标准普尔500指数进行多步预测,使用两种先进的神经网络方法:时态Kolmogorov-Arnold网络(TKAN)和长短期记忆(LSTM)。
长短期记忆(LSTM):
LSTMs 是一种循环神经网络(RNNs)的变体,在时间序列预测中已经被确立为标准。它们以其处理长期依赖关系和解决梯度消失问题的能力而闻名,因此它们成为了多步预报的流行选择。对于那些模式依赖于过去事件的复杂且非线性的时间序列,LSTMs 在这些情况下特别有用,例如股市数据。
研究的目的:本研究中,我们将两种技术(TKAN和LSTM)应用于标普500指数的历史数据,目的是进行多步向前预测。具体来说,我们将研究以下预测时间点:1, 2, 3, 5, 6, 7, 10和12步向前。这将使我们能够观察到,随着我们尝试预测的未来步数增多,模型的表现如何变化,并且对于每个预测时间点,我们将分别评估均方误差(MSE)和 决定系数 (R²)。
The R² 被定义为:衡量因变量变化中有多少比例可以被模型解释。
其中 _yi 是实际值,分子中的另一个变量是模型的预测值,分母中的变量则是实际值的平均值。
在本研究中,R² 将用来表示我们的模型(TKAN 和 LSTM)解释标准普尔500指数价格波动的准确性。当 R² 值接近 1 时,表示模型能够以高精度预测值;而接近 0 或为负值则表明模型预测效果不佳,甚至比平均水平差。
这两种方法的比较将让我们来评估哪一种方法在预测准确度方面表现更优。此外,我们将分析每种模型在不同的预测时间段上的泛化能力和捕捉市场模式的能力,从而清楚地展示这两种模型在多步预测中的表现优缺点。
解释代码本节将展示所使用的代码,并解释它是如何工作的。
- 图书馆和数据清理:
我们导入所需的库,并从该网站获取SP500(标普500)数据。
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
from tkan import TKAN # TKAN is a custom module
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM
from tensorflow.keras.optimizers import Adam
from sklearn.metrics import mean_squared_error, r2_score
seed = 42 # 设置随机种子
np.random.seed(seed)
tf.random.set_seed(seed) # 设置 TensorFlow 的随机种子
random.seed(seed)
data = pd.read_csv('sp500.csv')
data['最后'] = data['最后'].apply(lambda x: float(str(x).replace(',', '')) * 1000) # 将数值转换为浮点数并乘以1000
data['日期'] = pd.to_datetime(data['日期']) # 转换日期格式
data = data.sort_values(by='日期', ascending=True).reset_index(drop=True) # 按日期排序
data_series = data['最后'].values.reshape(-1, 1) # 数据序列2. 数据建模:
首先,使用 MinMaxScaler 对时间序列值进行归一化处理,将数据缩放至0到1之间。然后,定义时间窗口大小(_windowsize)和预测时长(_future_stepslist)。根据这些参数生成输入序列X和输出标签y:X包含20步长的滑动窗口,而y包含根据 _future_stepslist 中定义的未来步长预测的值。数据被分为训练集(80%)和测试集(20%),并将每组的日期保存下来以供后续分析。
scaler = MinMaxScaler() # 定义归一化器
data_序列缩放 = scaler.fit_transform(data_series) # 对数据序列进行缩放
窗口大小 = 20 # 定义窗口大小
未来步数列表 = [1, 2, 3, 5, 6, 7, 10, 12] # 定义未来步数列表
结果 = [] # 初始化结果列表
for 未来步数 in 未来步数列表: # 遍历未来步数列表
X, y = [], [] # 初始化X和y列表
for i in range(len(data_序列缩放) - 窗口大小 - 未来步数 + 1): # 遍历数据序列
X.append(data_序列缩放[i:i + 窗口大小]) # 将数据添加到X列表中
y.append(data_序列缩放[i + 窗口大小:i + 窗口大小 + 未来步数].flatten()) # 将数据添加到y列表中
X = np.array(X) # 将X转换为numpy数组
y = np.array(y) # 将y转换为numpy数组
分割索引 = int(len(X) * 0.8) # 计算训练集和测试集的分割索引
X_train, X_test = X[:分割索引], X[分割索引:] # 分割X为训练集和测试集
y_train, y_test = y[:分割索引], y[分割索引:] # 分割y为训练集和测试集
fechas_train = data['Fecha'].iloc[窗口大小:分割索引 + 窗口大小].values # 获取训练集的日期
fechas_test = data['Fecha'].iloc[分割索引 + 窗口大小:分割索引 + 窗口大小 + len(y_test)].values # 获取测试集的日期3. TKAN模型的搭建和训练:
The TKAN 模型 是使用序列架构构建和训练的,该架构包含一个 TKAN 层,后面跟着一个全连接层,用于预测多个未来的步骤。该模型使用 Adam 优化器和均方误差(MSE)损失进行编译。训练后,在测试集上进行预测并反归一化处理预测和实际值,将预测和实际值恢复到原始尺度。
model_tkan = Sequential([
TKAN(200, sub_kan_configs=[{'spline_order': 4, 'grid_size': 12}, {'spline_order': 3, 'grid_size': 10}, {'spline_order': 5, 'grid_size': 8}],
return_sequences=False, use_bias=True),
Dense(units=future_steps, activation='linear')
])
model_tkan.compile(optimizer=Adam(learning_rate=0.001), loss='mse')
history_tkan = model_tkan.fit(X_train, y_train, epochs=50, batch_size=32, validation_split=0.2)
y_pred_tkan = model_tkan.predict(X_test)
y_test_inverse = scaler.inverse_transform(y_test)
y_pred_tkan_inverse = scaler.inverse_transform(y_pred_tkan)4. 构建和训练LSTM模型:
The LSTM 模型 的构建和训练方式与 TKAN 类似,使用一个 LSTM 层后跟一个全连接层来预测多个时间步。然后,在测试集上进行预测时,反向归一化以恢复原始的数值范围。
model_lstm = Sequential([
LSTM(200, input_shape=(X_train.shape[1], X_train.shape[2]), return_sequences=False),
Dense(units=future_steps, activation='linear')
])
model_lstm.compile(optimizer='adam', loss='mse')
history_lstm = model_lstm.fit(X_train, y_train, epochs=50, batch_size=32, validation_split=0.2)
y_pred_lstm = model_lstm.predict(X_test)
y_pred_lstm_inverse = scaler.inverse_transform(y_pred_lstm)5. 模型评估和结果保存:
mse_tkan = mean_squared_error(y_test_inverse, y_pred_tkan_inverse)
r2_tkan = r2_score(y_test_inverse, y_pred_tkan_inverse)
mse_lstm = mean_squared_error(y_test_inverse, y_pred_lstm_inverse)
r2_lstm = r2_score(y_test_inverse, y_pred_lstm_inverse)
results.append({
'future_steps': future_steps,
'R^2 TKAN': r2_tkan,
'R^2 LSTM': r2_lstm
})
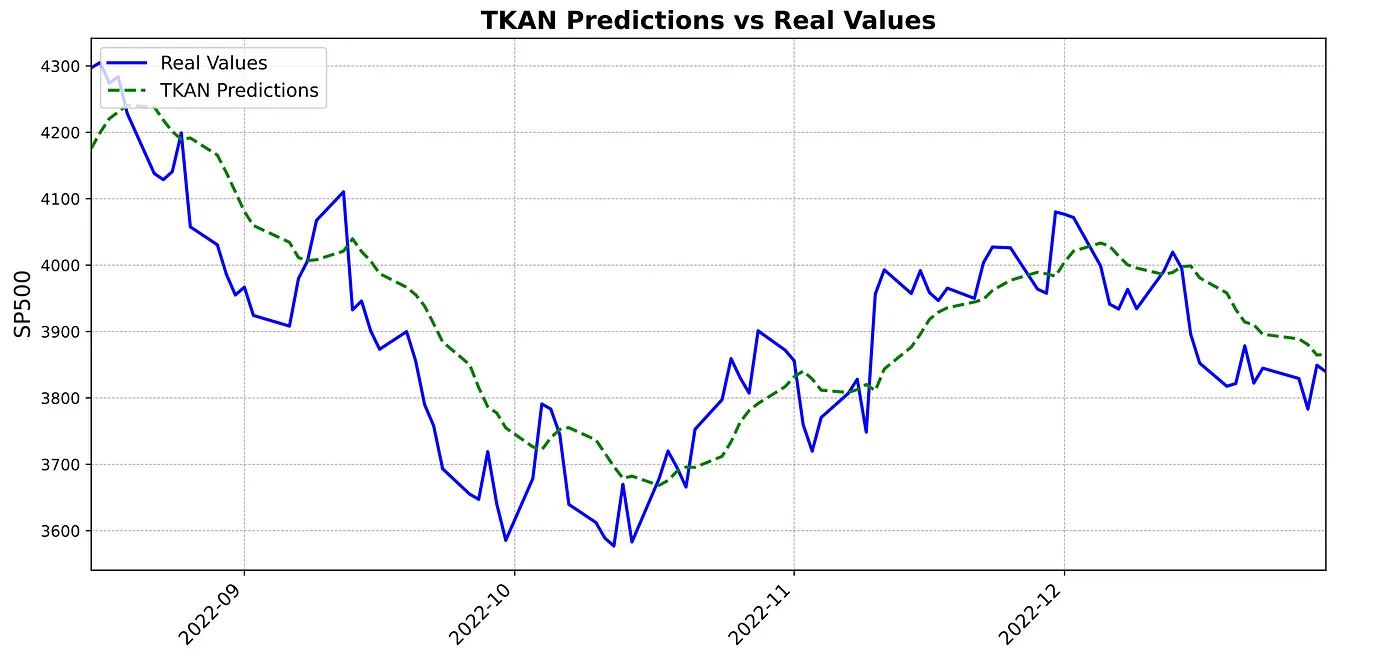
results_df = pd.DataFrame(results)接下来我们要展示的是,利用TKAN和LSTM模型对S&P 500指数进行多步预测分析的结果。我们生成了1步情况下的图表,以帮助可视化并比较两种模型在不同预测视角下的表现。
这张图表比较了TKAN模型(绿色虚线预测)所做的预测与实际的S&P 500指数值(实线蓝色线)。从这张图表中可以看出,虽然在更剧烈的波动中有所平滑,TKAN模型基本上跟随了指数的趋势。
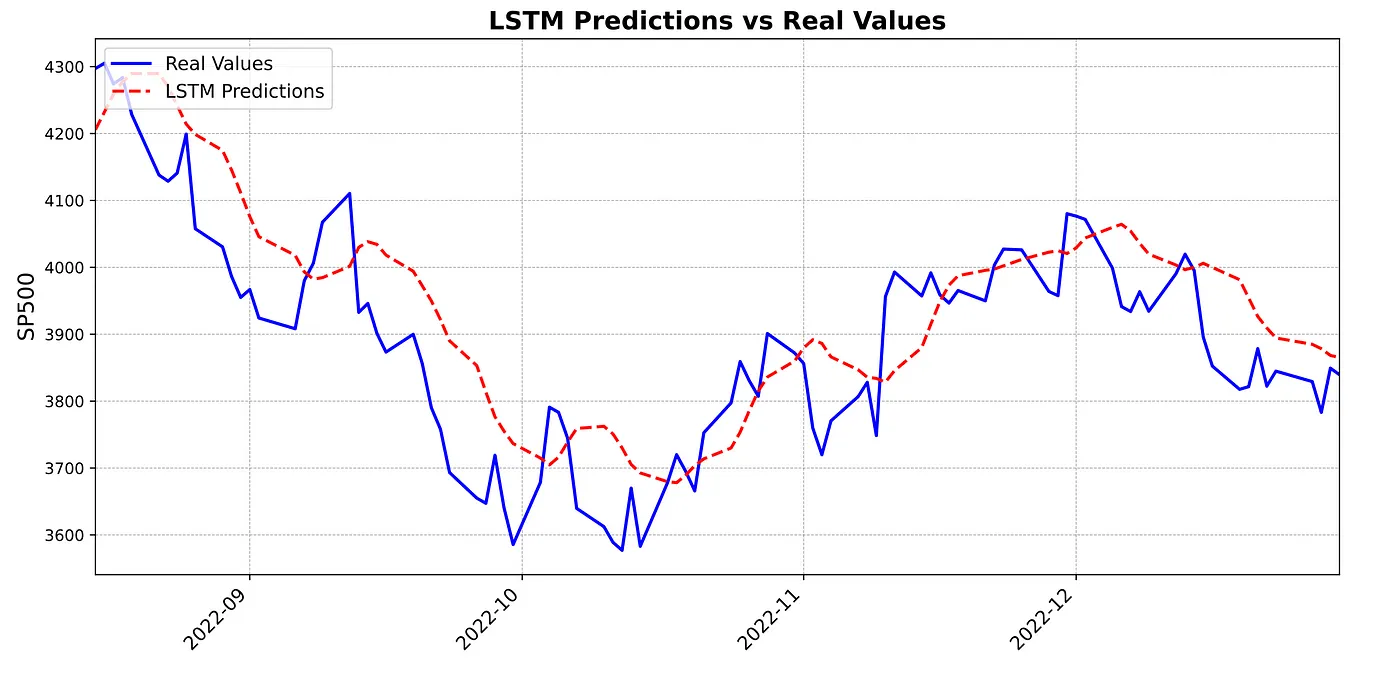
在这个第二个图表中,用红色虚线表示了由LSTM模型生成的预测结果,并与实际的S&P 500指数进行了比较。
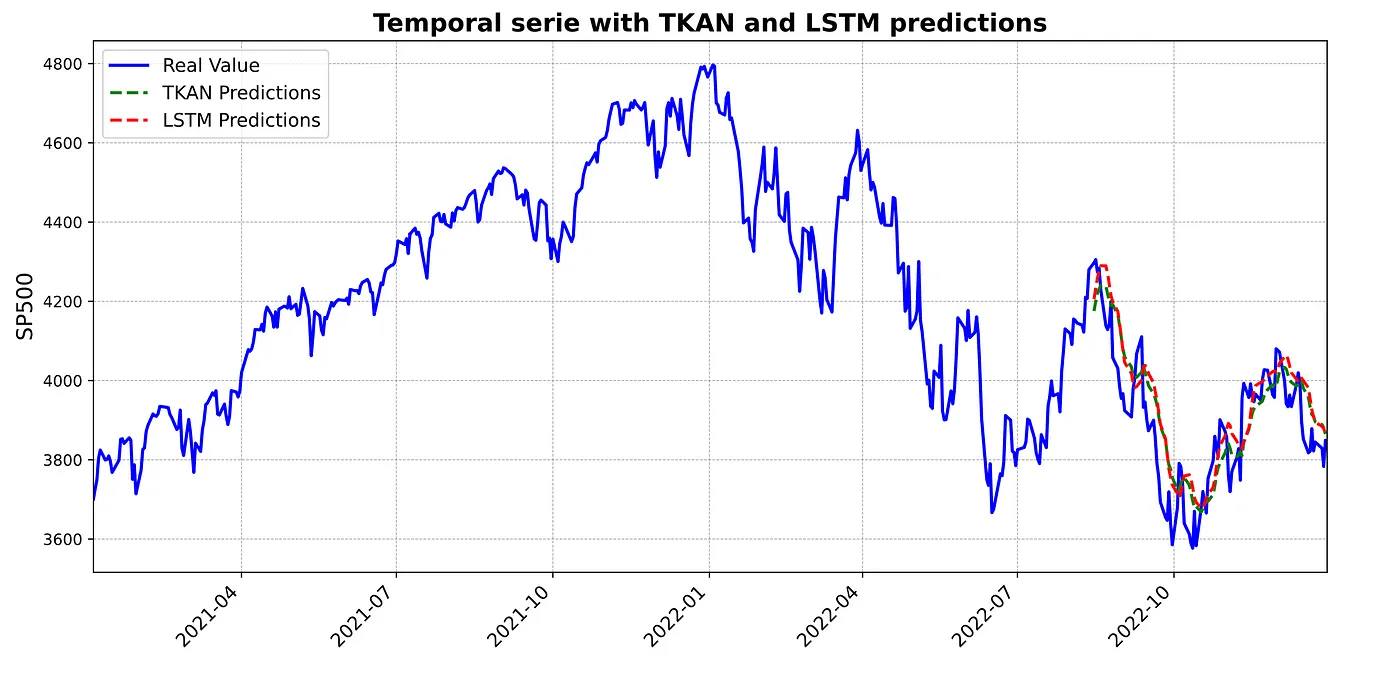
第三个图表将两种模型的预测(TKAN模型用绿色表示,LSTM模型用红色表示)与实际的标普500指数值(用蓝色表示)结合在一起。从这张图中,让我们看到这两种模型如何捕捉(标普500)指数的不同波动,这发生在较长的一段时间内。
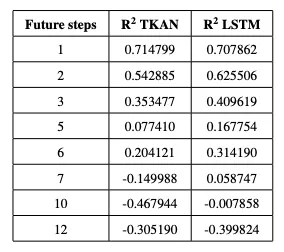
R² 结果分析在本节中,我们展示了不同步长的 R² 系数结果展示。通过这种方式,可以看出我们的模型能多好地解释 SP500 的变化,这取决于上述提到的预测的程度。
所得的结果表明,TKAN网络在R²方面并不一致优于LSTM。两个模型之间的比较显示,在某些预测时长表现更佳,而在其他时长则不然。在关于TKAN的原始研究[2]中,使用比特币数据集进行了类似的测试,得出结论认为,对于长期预测,TKAN优于LSTM,而对于短期预测,两者表现相似。然而,在我们的案例中,并没有观察到同样的行为,这可能是因为我们的网络配置不同。在原始研究中,为TKAN和LSTM都使用了更复杂的多层架构,而在本次分析中,我们仅使用了单层架构。
此外,我还测试了增加更多层来提高模型的复杂度,但并没有发现显著的性能提升。然而,值得注意的是,TKAN网络在某些预测时间段甚至在某些时间段的表现超越了LSTM,这是项相当显著的成就。可能我们研究中使用的有限数据量对TKAN的训练产生了负面影响,这可能部分解释了我们结果与原研究结果的不同。
TKANs在捕捉复杂的时间变化方面很有前景,这使它们在金融、能源和天气预报等领域具有很大的应用价值。它们改善长期预测的能力及其可以灵活地整合到混合模型中的潜力,在异常检测和流程优化等领域的应用潜力巨大。未来的研究可以进一步探索它们在各种领域中更准确和更稳健的预测系统中的应用。
参考书目[1] 刘, Z., 王, Y., 刘迪亚, S., 鲁厄尔, F., 霍尔夫森, J., 萨尔贾奇克, M., 侯, T. Y., & 特格马克, M., 2024. KAN: Kolmogorov-Arnold Networks. https://arxiv.org/abs/2404.19756
[2] Genet, R., & Inzirillo, H. (2024). TKAN: 时间Kolmogorov-Arnold网络. arXiv预印本 arXiv:2405.07344.
共同学习,写下你的评论
评论加载中...
作者其他优质文章