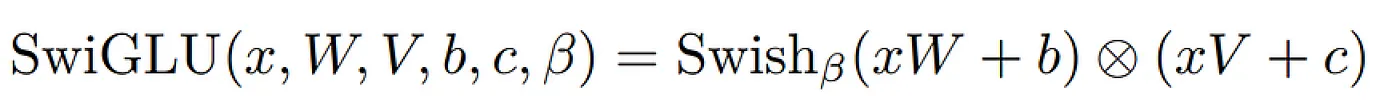LLaMA 3 是继 Mistral 之后最令人期待的开源模型之一,能够解决各种任务。我之前在 Medium 上写了一篇博客,介绍了如何从零开始使用 LLaMA 架构创建一个参数超过 230 万的大型语言模型。现在 LLaMA-3 发布了,我们将以更简单的方式重新创建它。
我们这篇博客不会使用 GPU,但你需要至少 17 GB 的内存,因为我们将会加载一些超过 15 GB 大小的文件。如果你的内存不足,可以使用 Kaggle 作为解决方案。由于我们不需要 GPU,Kaggle 提供了在仅使用 CPU 核心作为加速器的情况下,提供 30 GB 的内存。
为了避免从这篇博客中复制粘贴代码,这里提供了包含所有代码和信息的笔记本文件的GitHub仓库:
GitHub - FareedKhan-dev/Building-llama3-from-scratch: LLaMA 3 是 Mistral 之后最令人期待的开源模型之一,我们将用更简单的方式重现其架构…github.com这里是一个博客链接,它会指导你如何从零开始创建一个拥有2.3百万参数的大型语言模型(LLM):
从零开始使用Python构建百万参数的LLM一步一步指导复制LLaMA架构levelup.gitconnected.com 目录-
前提条件
-
LLaMA 2 和 LLaMA 3 的区别
-
理解 LLaMA 3 的 Transformer 架构
∘ 使用 RMSNorm 的预归一化
∘ SwiGLU 激活函数
∘ Rotary Embeddings (RoPE)
∘ Byte Pair Encoding (BPE) 算法 -
设置舞台
-
理解文件结构
-
对输入数据进行分词
-
为每个分词创建嵌入
-
使用 RMSNorm 进行归一化
-
注意力头(Query、Key、Values)
-
实现 RoPE
-
实现自注意力
-
实现多头注意力
-
实现 SwiGLU 激活函数
-
合并所有内容
- 生成输出
好的部分是我们不会使用面向对象编程(OOP)的编码,只需要使用普通的Python编程。但是,你应该对神经网络和Transformer架构有一个基本的了解。这是跟随这篇博客所需的唯一两个前提条件。
LLaMA 2 和 LLaMA 3 之间的区别在深入了解技术细节之前,你首先需要知道的是LLaMA 3 的整个架构与 LLaMA 2 完全相同。因此,如果你还没有了解过 LLaMA 3 的技术细节,也不必担心,你可以顺利跟随这篇博客。即使你对 LLaMA 2 的架构没有了解,也不用担心,我们也会对它的技术细节进行高层次的概述。无论哪种情况,这篇博客都是为你准备的。
这里是一些关于 LLaMA 2 和 LLaMA 3 的关键点。如果你已经熟悉它们的架构:
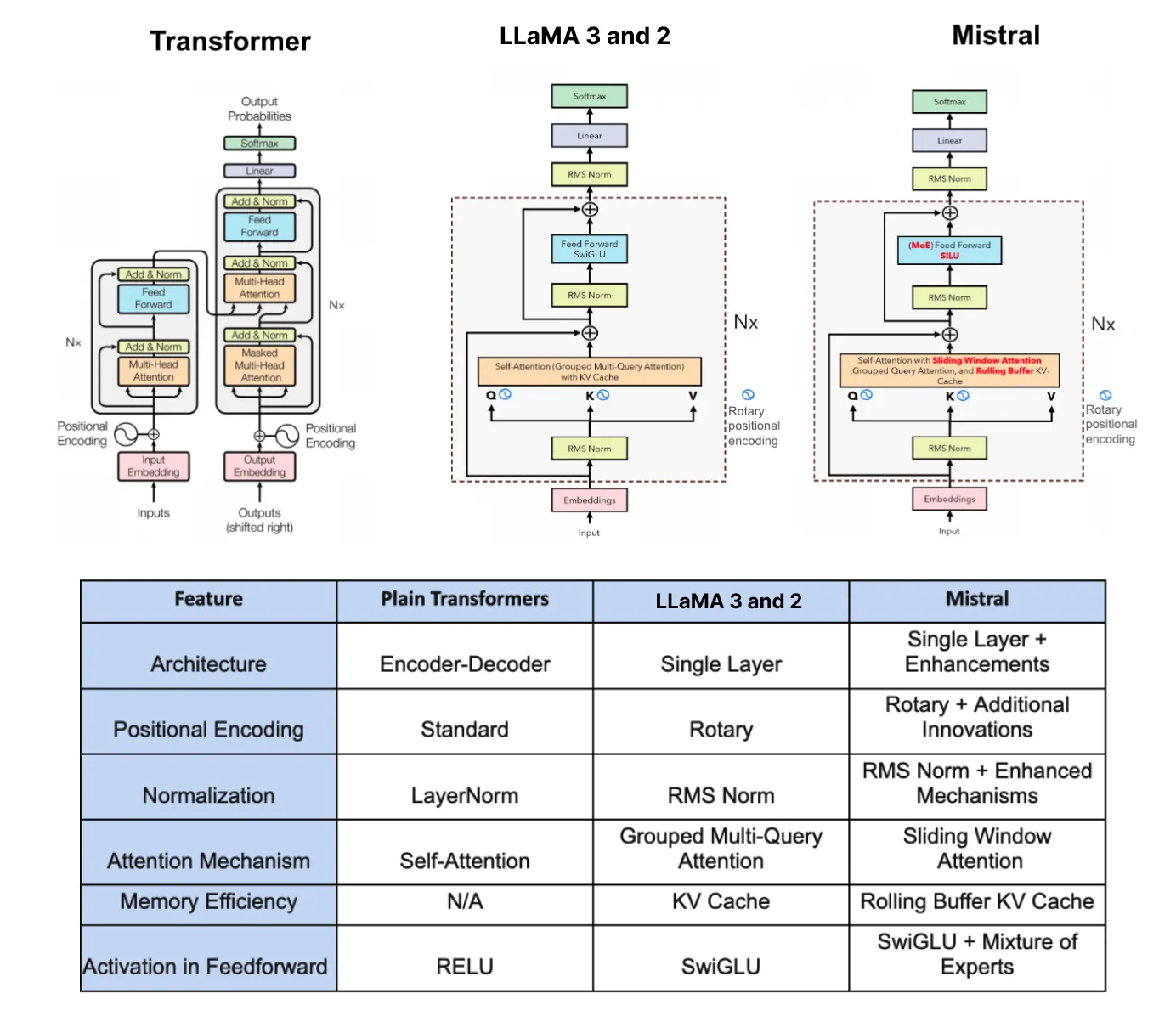
理解LLaMA 3的Transformer架构理解 LLaMA 3 的架构在开始编码之前非常重要。为了更好地视觉理解,这里有一个 vanilla Transformer、LLaMA 2/3 和 Mistral 之间的对比图。
让我们更详细地了解一下 LLaMA 3 的最重要组件:
1. 使用RMSNorm进行预归一化:在 LLaMA 3 方法中,与 LLaMA 2 相同,使用了一种称为 RMSNorm 的技术来对每个变压器子层的输入进行规范化。
想象你正在为一场重要的考试做准备,你有一本厚厚的教科书,里面包含了许多章节。每一章代表一个不同的主题,但有些章节对于理解这门学科来说比其他章节更为关键。
现在,在深入整个教材之前,你决定评估每一章的重要性。你不想每章都花费相同的时间;你希望更专注于关键的章节。
这就是预归一化使用RMSNorm发挥作用的地方,特别是在像ChatGPT这样的大型语言模型中。这就像根据每章的重要性为其分配一个权重。对于主题基础章节分配更高的权重,而对不太重要的章节分配较低的权重。
所以在深入学习之前,你会根据每个章节的权重重要性来调整学习计划。你为权重较高的章节分配更多的时间和精力,确保彻底掌握核心概念。
均方根层归一化论文 (https://arxiv.org/abs/1910.07467)
同样地,使用RMSNorm进行预归一化有助于大语言模型优先处理哪些部分的文本对理解上下文和含义更为关键。它为重要的元素分配更高的权重,为不太关键的元素分配较低的权重,确保模型将注意力集中在最需要的地方,以实现准确的理解。感兴趣的读者可以在这里探索RMSNorm的详细实现这里。
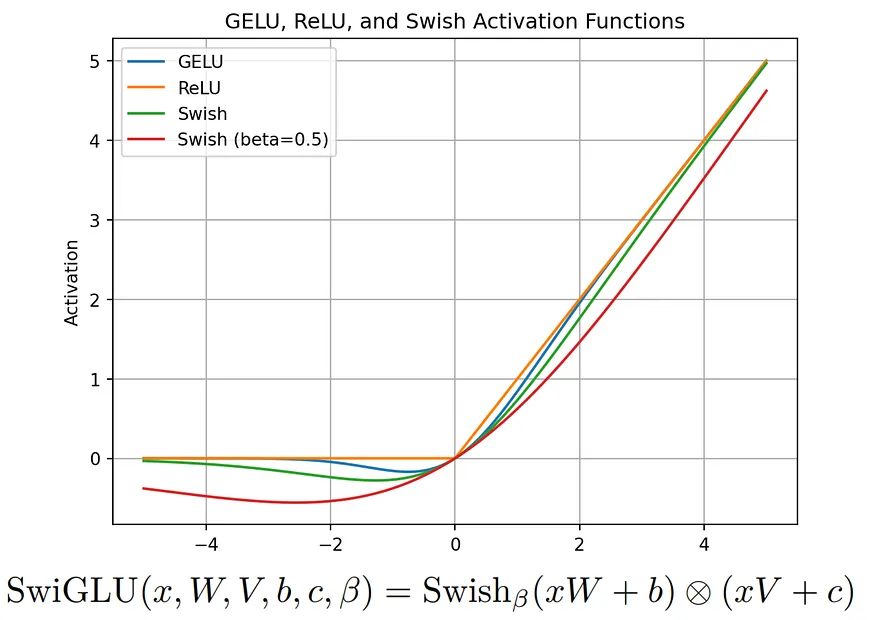
2. SwiGLU 激活函数:LLaMA 引入了 SwiGLU 激活函数,借鉴了 PaLM 的设计。
想象一下你是一名老师,正在尝试向学生解释一个复杂的主题。你有一个大白板,在上面写下关键点并绘制图表,以便让学生更容易理解。但有时候,你的字迹可能不够工整,或者你的图表可能画得不够完美。这可能会让学生更难理解材料。
现在,想象一下如果你有一支魔法笔,这支笔会根据每个要点的重要性自动调整字体大小和样式。如果某个要点非常重要,这支笔会写得更大更清晰,让它更加突出。如果某个要点不太重要,这支笔会写得更小,但仍然可以辨认。
SwiGLU 就像是为大型语言模型(如 ChatGPT)准备的神奇笔。在生成文本之前,SwiGLU 根据每个词或短语与上下文的相关性调整其重要性。就像神奇笔可以调整你的书写大小和风格一样,SwiGLU 也可以调整每个词或短语的强调程度。
SwiGLU: GLU 变体改进 Transformer (https://kikaben.com/swiglu-2020/)
因此,当大语言模型生成文本时,它可以更突出重要的部分,使其更加显眼,并确保它们对整个文本的理解做出更大贡献。这样,SwiGLU 帮助大语言模型生成更清晰、更容易理解的文本,就像魔法笔帮助你在白板上为学生创造更清晰的解释一样。有关 SwiGLU 的更多细节可以在相关 论文 中找到。
3. 旋转嵌入(RoPE):RoPE(Rotary Embeddings)是 LLaMA 3 中使用的一种位置嵌入类型。
想象你在一个教室里,想要为学生分配座位进行小组讨论。通常,你可能会将座位排列成行和列,每个学生都有固定的位置。然而,在某些情况下,你希望创建一个更灵活的座位安排,让学生可以自由移动和互动。
RoPE 就像一种特殊的座位安排,允许学生旋转并改变位置,同时仍然保持彼此之间的相对位置。学生不再固定在一个位置,而是可以以圆形运动的方式移动,从而实现更加流畅的互动。
在这个场景中,每个学生代表文本序列中的一个单词或标记,他们的位置对应于他们在序列中的位置。就像 ROPE 允许学生旋转并改变位置一样,ROPE 允许文本序列中单词的位置嵌入根据它们彼此之间的相对位置动态变化。
因此,在处理文本时,ROPE 并没有将位置嵌入视为固定和静态的,而是引入了旋转的特性,使得能够更灵活地表示序列中单词之间的动态关系。这种灵活性有助于像 ChatGPT 这样的模型更好地理解和生成自然流畅且保持连贯性的文本,就像动态的座位安排促进了课堂上更互动的讨论一样。有兴趣了解数学细节的人可以参考 RoPE 论文。
4. 字符对编码(BPE)算法LLaMA 3 使用由 OpenAI 引入的 tiktoken 库中的 Byte Pair Encoding (BPE),而 LLaMA 2 的分词器 BPE 则基于 sentencepiece 库。它们之间存在一些细微差别,但首先,让我们了解一下 BPE 究竟是什么。
让我们从一个简单的例子开始。假设我们有一个文本语料库,其中包含单词:“ab”,“bc”,“bcd”和“cde”。我们首先用文本语料库中的所有单个字符初始化词汇表,因此我们的初始词汇表是 {“a”,“b”,“c”,“d”,“e”}。
接下来,我们计算文本语料库中每个字符的频率。在我们的例子中,频率为:{“a”: 1, “b”: 3, “c”: 3, “d”: 2, “e”: 1}。
现在,我们开始合并过程。我们重复以下步骤,直到我们的词汇表达到所需的大小:
- 首先,我们找到最频繁的连续字符对。在这种情况下,最频繁的字符对是“bc”,出现次数为2。然后我们将这对字符合并,创建一个新的子词单元“bc”。合并后,我们更新频率计数以反映新的子词单元。更新后的频率为 {“a”: 1, “b”: 2, “c”: 2, “d”: 2, “e”: 1, “bc”: 2}。我们将新的子词单元“bc”添加到词汇表中,词汇表现在变为 {“a”, “b”, “c”, “d”, “e”, “bc”}。
- 我们重复该过程。下一个最频繁的字符对是“cd”。我们将“cd”合并为新的子词单元“cd”,并更新频率计数。更新后的频率为 {“a”: 1, “b”: 2, “c”: 1, “d”: 1, “e”: 1, “bc”: 2, “cd”: 2}。我们将“cd”添加到词汇表中,词汇表变为 {“a”, “b”, “c”, “d”, “e”, “bc”, “cd”}。
- 继续该过程,下一个最频繁的字符对是“de”。我们将“de”合并为子词单元“de”,并更新频率计数为 {“a”: 1, “b”: 2, “c”: 1, “d”: 1, “e”: 0, “bc”: 2, “cd”: 1, “de”: 1}。我们将“de”添加到词汇表中,词汇表变为 {“a”, “b”, “c”, “d”, “e”, “bc”, “cd”, “de”}。
- 接下来,我们找到最频繁的字符对“ab”。我们将“ab”合并为子词单元“ab”,并更新频率计数为 {“a”: 0, “b”: 1, “c”: 1, “d”: 1, “e”: 0, “bc”: 2, “cd”: 1, “de”: 1, “ab”: 1}。我们将“ab”添加到词汇表中,词汇表变为 {“a”, “b”, “c”, “d”, “e”, “bc”, “cd”, “de”, “ab”}。
- 然后,下一个最频繁的字符对是“bcd”。我们将“bcd”合并为子词单元“bcd”,并更新频率计数为 {“a”: 0, “b”: 0, “c”: 0, “d”: 0, “e”: 0, “bc”: 1, “cd”: 0, “de”: 1, “ab”: 1, “bcd”: 1}。我们将“bcd”添加到词汇表中,词汇表变为 {“a”, “b”, “c”, “d”, “e”, “bc”, “cd”, “de”, “ab”, “bcd”}。
- 最后,最频繁的字符对是“cde”。我们将“cde”合并为子词单元“cde”,并更新频率计数为 {“a”: 0, “b”: 0, “c”: 0, “d”: 0, “e”: 0, “bc”: 1, “cd”: 0, “de”: 0, “ab”: 1, “bcd”: 1, “cde”: 1}。我们将“cde”添加到词汇表中,词汇表变为 {“a”, “b”, “c”, “d”, “e”, “bc”, “cd”, “de”, “ab”, “bcd”, “cde”}。
这项技术可以提升大语言模型的性能,并且能够处理罕见和不在词汇表中的单词。TikToken BPE 与 sentencepiece BPE 的主要区别在于,TikToken BPE 并不是总是将整个单词拆分成更小的部分,如果整个单词已经在词汇表中。例如,如果 “hugging” 在词汇表中,它将保持为一个 token,而不是拆分成 [“hug”,”ging”]。
设置舞台我们将使用一小部分Python库,但最好安装这些库以避免遇到 “未找到模块” 错误。
pip install sentencepiece tiktoken torch blobfile matplotlib huggingface_hub安装所需的库之后,我们需要下载一些文件。由于我们要复制 llama-3–8B 的架构,因此您必须在 HuggingFace 上拥有一个账户。此外,由于 llama-3 是一个受保护的模型,您需要接受他们的服务条款才能访问模型内容。
以下是步骤:
完成这两个步骤之后,现在我们需要下载一些文件。有两种方式可以做到这一点:
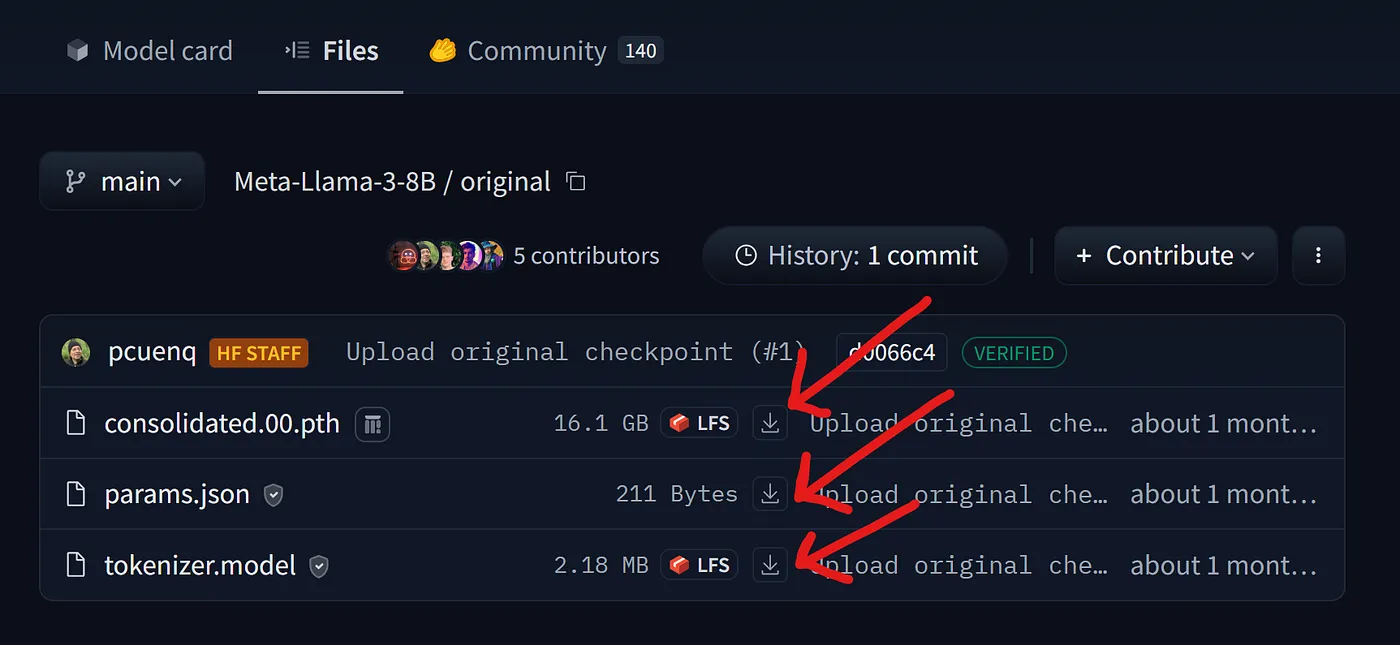
(选项1:手动) 从这个 链接 进入 llama-3–8B HF 目录,并手动下载这三个文件。
下载 LLaMA-3 配置文件
(选项 2:编码) 我们可以使用之前安装的 hugging_face 库来下载所有这些文件。但是首先,我们需要使用我们的 HF Token 在工作笔记本中登录到 HuggingFace Hub。你可以创建一个新的 token 或从这个 链接 访问它。
# 从 `huggingface_hub` 模块导入 `notebook_login` 函数。
from huggingface_hub import notebook_login
# 执行 `notebook_login` 函数以登录到 Hugging Face Hub。
notebook_login()运行完这个单元格后,它会要求你输入token。如果登录时出现错误,请重试,但确保取消选中add token as git credential.之后,我们只需要运行一个简单的Python代码来下载构成llama-3–8B架构的三个文件。
# 从 huggingface_hub 库中导入必要的函数
from huggingface_hub import hf_hub_download
# 定义仓库信息
repo_id = "meta-llama/Meta-Llama-3-8B"
subfolder = "original" # 指定仓库中的子文件夹
# 要下载的文件名列表
filenames = ["params.json", "tokenizer.model", "consolidated.00.pth"]
# 指定要保存下载文件的目录
save_directory = "llama-3-8B/" # 用您希望的路径替换
# 下载每个文件
for filename in filenames:
hf_hub_download(
repo_id=repo_id, # 仓库 ID
filename=filename, # 要下载的文件名
subfolder=subfolder, # 仓库中的子文件夹
local_dir=save_directory # 保存下载文件的目录
)一旦所有文件下载完毕,我们就需要导入将在本博客中使用的库。
# 分词库
import tiktoken
# BPE 加载函数
from tiktoken.load import load_tiktoken_bpe
# PyTorch 库
import torch
# JSON 处理
import json接下来,我们需要了解每个文件将用于什么。
理解文件结构由于我们旨在精确复制 llama-3,这意味着我们的输入文本必须产生有意义的输出。例如,如果我们的输入是 “太阳的颜色是?” ,那么输出必须是 “白色” 。实现这一点需要在大型数据集上训练我们的大语言模型,这需要强大的计算能力,对于我们来说是不可行的。
然而,Meta 已经公开发布了他们的 llama-3 架构文件,或者说更复杂一点,就是他们的预训练权重,供使用。我们刚刚下载了这些文件,这使我们能够在无需训练或大量数据集的情况下复制他们的架构。一切都已经准备好了,我们只需要在正确的位置使用正确的组件即可。
查看这些文件及其重要性:
tokenizer.model — 如我们之前讨论的,LLaMA-3 使用来自 tiktoken 的 Byte Pair Encoding (BPE) 分词器,该分词器是在一个包含 15 万亿个 token 的数据集上训练的 —— 这个数据集比用于 LLaMA-2 的数据集大 7 倍。让我们加载这个文件并看看它包含什么。
# 从 llama-3-8B 加载分词器
tokenizer_model = load_tiktoken_bpe("tokenizer.model")
# 获取分词器模型的长度
len(tokenizer_model)
# 输出: 128000
# 获取 `tokenizer_model` 对象的类型
type(tokenizer_model)
# 输出: 字典length 属性显示了词汇表的总大小,即训练数据中字符的唯一数量。tokenizer_model 的类型是一个字典。
# 打印 tokenizer 模型的前 10 个项目
dict(list(tokenizer_model.items())[5600:5610])
#### 输出 ####
{
b'mitted': 5600,
b" $('#": 5601,
b' saw': 5602,
b' approach': 5603,
b'ICE': 5604,
b' saying': 5605,
b' anyone': 5606,
b'meta': 5607,
b'SD': 5608,
b' song': 5609
}
#### 输出 ####当我们打印出其中的10个随机项时,你会看到使用BPE算法形成的字符串,类似于我们之前讨论的例子。键代表BPE训练中的字节序列,而值则代表基于频率的合并等级。
consolidated.00.pth — 包含 Llama-3–8B 的学习参数(权重)。这些参数包括模型理解和处理语言的信息,例如它如何表示词元、计算注意力、执行前向变换以及规范化其输出。
# 加载 LLaMA-3-8B 的 PyTorch 模型
model = torch.load("consolidated.00.pth")
# 打印架构的前 11 层
list(model.keys())[:11]
#### 输出 ####
[
'tok_embeddings.weight',
'layers.0.attention.wq.weight',
'layers.0.attention.wk.weight',
'layers.0.attention.wv.weight',
'layers.0.attention.wo.weight',
'layers.0.feed_forward.w1.weight',
'layers.0.feed_forward.w3.weight',
'layers.0.feed_forward.w2.weight',
'layers.0.attention_norm.weight',
'layers.0.ffn_norm.weight',
'layers.1.attention.wq.weight',
]
#### 输出 ####如果你熟悉变压器架构,你就会知道查询矩阵、键矩阵等。稍后,我们将使用这些层/权重在Llama-3的架构中创建这样的矩阵。
params.json— 包含各种参数值,例如:
# 打开参数 JSON 文件
with open("params.json", "r") as f:
config = json.load(f)
# 打印内容
print(config)
#### 输出 ####
{
'dim': 4096,
'n_layers': 32,
'n_heads': 32,
'n_kv_heads': 8,
'vocab_size': 128256,
'multiple_of': 1024,
'ffn_dim_multiplier': 1.3,
'norm_eps': 1e-05,
'rope_theta': 500000.0
}
#### 输出 ####这些值将帮助我们通过指定诸如头数、嵌入向量维度等细节来复现Llama-3架构。
让我们把这些值存储起来,以便以后使用。
# 维度
dim = config["dim"]
# 层数
n_layers = config["n_layers"]
# 头数
n_heads = config["n_heads"]
# KV头数
n_kv_heads = config["n_kv_heads"]
# 词汇量
vocab_size = config["vocab_size"]
# 多重
multiple_of = config["multiple_of"]
# 前馈网络维度乘数
ffn_dim_multiplier = config["ffn_dim_multiplier"]
# 归一化epsilon
norm_eps = config["norm_eps"]
# RoPE
rope_theta = torch.tensor(config["rope_theta"])现在我们有了分词器模型、包含权重的架构模型和配置参数,让我们从零开始编写自己的 Llama-3。
对输入数据进行分词我们首先需要做的是将输入文本转换为令牌,为此我们首先必须创建一些特殊的令牌,这些令牌对于在分词后的文本中提供结构化的标记是必要的,从而使分词器能够识别和处理特定的条件或指令。
special_tokens = [
"", # 标记文本序列的开始。
"", # 标记文本序列的结束。
"", # 为将来预留。
"", # 为将来预留。
"", # 为将来预留。
"", # 为将来预留。
"", # 表示头部ID的开始。
"", # 表示头部ID的结束。
"", # 为将来预留。
"", # 标记一轮对话的结束(在对话上下文中)。
] + [f"" for i in range(5, 256 - 5)] # 为将来预留的一大批token。接下来我们定义将文本分割成令牌的规则,通过指定不同的模式来匹配输入文本中的各种类型的子字符串。这是实现的方法。
# 用于将文本拆分成令牌的模式
tokenize_breaker = r"(?i:'s|'t|'re|'ve|'m|'ll|'d)|[^\r\n\p{L}\p{N}]?\p{L}+|\p{N}{1,3}| ?[^\s\p{L}\p{N}]+[\r\n]*|\s*[\r\n]+|\s+(?!\S)|\s+"它可以提取输入文本中的单词、缩写、最多三位数的数字以及非空白字符序列,您可以根据需求自定义它。
我们需要编写一个简单的分词器函数,使用TikToken BPE,该函数接受三个输入:tokenizer_model、tokenize_breaker和special_tokens。该函数将根据需要对输入文本进行编码/解码。
# 使用指定参数初始化分词器
tokenizer = tiktoken.Encoding(
# 确保设置 tokenizer.model 文件的路径
name = "tokenizer.model",
# 定义分词模式字符串
pat_str = tokenize_breaker,
# 从 LLaMA-3 的 tokenizer_model 中分配 BPE 合并等级
mergeable_ranks = tokenizer_model,
# 使用索引设置特殊标记
special_tokens={token: len(tokenizer_model) + i for i, token in enumerate(special_tokens)},
)
# 对 "hello world!" 进行编码,然后将标记解码为字符串
tokenizer.decode(tokenizer.encode("hello world!"))
#### 输出 ####
hello world!
#### 输出 ####为了验证我们的编码函数方法是否正确工作,我们将“Hello World”传递给它。首先,它将文本编码,将其转换为数值。然后,它将这些数值解码回文本,结果为“hello world!”。这确认了函数工作正确。让我们对输入进行分词。
# 输入提示
prompt = "the answer to the ultimate question of life, the universe, and everything is "
# 使用 tokenizer 对提示进行编码,并在前面添加一个特殊 token (128000)
tokens = [128000] + tokenizer.encode(prompt)
print(tokens) # 打印编码后的 tokens
# 将 tokens 列表转换为 PyTorch 张量
tokens = torch.tensor(tokens)
# 将每个 token 解码回对应的字符串
prompt_split_as_tokens = [tokenizer.decode([token.item()]) for token in tokens]
print(prompt_split_as_tokens) # 打印解码后的 tokens
#### 输出 ####
[128000, 1820, 4320, 311, ... ]
['', 'the', ' answer', ' to', ... ]
#### 输出 ####我们将输入文本 “the answer to the ultimate question of life, the universe, and everything is ” 以一个特殊 token 开始进行编码。
每个Token的嵌入创建如果我们检查输入向量的长度,它将会是:
# 检查输入向量的维度
len(tokens)
#### 输出 ####
17
#### 输出 #### # 检查来自 llama-3 架构的嵌入向量的维度
print(dim)
#### 输出 ####
4096
#### 输出 ####我们的输入向量目前为 (17x1) 维度,需要将其转换为每个分词单词的嵌入表示。这意味着我们的 (17x1) 令牌将变为 (17x4096),其中每个令牌对应一个长度为 4096 的嵌入。
# 定义嵌入层,指定词汇表大小和嵌入维度
embedding_layer = torch.nn.Embedding(vocab_size, dim)
# 将预训练的词嵌入复制到嵌入层
embedding_layer.weight.data.copy_(model["tok_embeddings.weight"])
# 获取给定词的嵌入,并转换为 torch.bfloat16 格式
token_embeddings_unnormalized = embedding_layer(tokens).to(torch.bfloat16)
# 打印生成的词嵌入的形状
token_embeddings_unnormalized.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####这些嵌入没有被归一化,如果我们不进行归一化,将会产生严重的影响。在下一节中,我们将对输入向量进行归一化处理。
使用RMSNorm进行规范化我们将使用之前看到的 RMSNorm 公式来规范化输入向量,以确保我们的输入已经被规范化。
均方根层归一化论文 (https://arxiv.org/abs/1910.07467)
# 计算RMSNorm
def rms_norm(tensor, norm_weights):
# 计算张量值沿最后一个维度的平方均值
squared_mean = tensor.pow(2).mean(-1, keepdim=True)
# 添加一个小值以避免除以零
normalized = torch.rsqrt(squared_mean + norm_eps)
# 将归一化后的张量与提供的归一化权重相乘
return (tensor * normalized) * norm_weights我们将使用来自layers_0的注意力权重来规范化我们的未规范化嵌入。使用layer_0的原因是我们现在正在创建我们LLaMA-3变压器架构的第一层。
# 使用RMS归一化以及提供的归一化权重
token_embeddings = rms_norm(token_embeddings_unnormalized,
model["layers.0.attention_norm.weight"])
# 打印生成的token嵌入的形状
token_embeddings.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####你可能已经知道维度不会发生变化,因为我们只是在对向量进行归一化处理,没有做其他操作。
注意力头(查询、键、值)首先,让我们从模型中加载查询、键、值和输出向量。
# 打印不同权重的形状
print(
# 查询权重形状
model["layers.0.attention.wq.weight"].shape,
# 键权重形状
model["layers.0.attention.wk.weight"].shape,
# 值权重形状
model["layers.0.attention.wv.weight"].shape,
# 输出权重形状
model["layers.0.attention.wo.weight"].shape
)
#### 输出 ####
torch.Size([4096, 4096]) # 查询权重维度
torch.Size([1024, 4096]) # 键权重维度
torch.Size([1024, 4096]) # 值权重维度
torch.Size([4096, 4096]) # 输出权重维度
#### 输出 ####这些维度表明我们下载的模型权重不是为每个头单独的,而是由于采用了并行方法/训练,为多个注意力头共同使用的。然而,我们可以将这些矩阵解包,使其仅适用于单个头。
# 获取注意力第一层的查询权重
q_layer0 = model["layers.0.attention.wq.weight"]
# 计算每头的维度
head_dim = q_layer0.shape[0] // n_heads
# 重塑查询权重以分离每头
q_layer0 = q_layer0.view(n_heads, head_dim, dim)
# 打印重塑后的查询权重张量的形状
q_layer0.shape
#### 输出 ####
torch.Size([32, 128, 4096])
#### 输出 ####在这里,32 是 Llama-3 中注意力头的数量,128 是查询向量的大小,4096 是 token 嵌入的大小。
我们可以使用以下方式访问第一层第一个头的查询权重矩阵:
# 提取注意力第一层第一个头的查询权重
q_layer0_head0 = q_layer0[0]
# 打印提取的查询权重张量的第一个头的形状
q_layer0_head0.shape
#### 输出 ####
torch.Size([128, 4096])
#### 输出 ####为了找到每个 token 的查询向量,我们将查询权重与 token 嵌入相乘。
# 矩阵乘法:token嵌入与查询权重的第一头的转置相乘
q_per_token = torch.matmul(token_embeddings, q_layer0_head0.T)
# 结果张量的形状:每个token的查询
q_per_token.shape
#### 输出 ####
torch.Size([17, 128])
#### 输出 ####查询向量本身不知道它们在提示中的位置,所以我们将会使用RoPE使它们意识到这一点。
实现RoPE我们将查询向量分成对,然后对每一对应用旋转角度偏移。
# 将每个查询的token转换为浮点数并拆分成对
q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2)
# 打印拆分成对后的张量形状
q_per_token_split_into_pairs.shape
#### 输出 ####
torch.Size([17, 64, 2])
#### 输出 ####我们有一个大小为 [17x64x2] 的向量,它表示将提示中的每个 token 的 128 长度查询拆分为 64 对。每一对将通过 m*theta 进行旋转,其中 m 是我们正在旋转查询的 token 的位置。
我们将使用复数的点积来旋转向量。
# 从0到1生成64个部分的值
zero_to_one_split_into_64_parts = torch.tensor(range(64))/64
# 打印生成的张量
zero_to_one_split_into_64_parts
#### 输出 ####
tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250,
0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656,
0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062,
0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469,
0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875,
0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281,
0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688,
0.9844])
#### 输出 ####在分割步骤之后,我们将计算其出现的频率。
# 使用幂运算计算频率
freqs = 1.0 / (rope_theta ** zero_to_one_split_into_64_parts)
# 显示结果频率
freqs
#### 输出 ####
tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01,
2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01,
8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02,
2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03,
7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03,
2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04,
6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04,
1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05,
5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05,
1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06,
4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06])
#### 输出 ####现在,对于每个令牌的查询元素使用复数,我们将查询转换为复数,然后根据它们的位置使用点积进行旋转。
# 将每个token的查询转换为复数
q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs)
q_per_token_as_complex_numbers.shape
# 输出: torch.Size([17, 64])
# 使用arange(17)和freqs的外积计算每个token的频率
freqs_for_each_token = torch.outer(torch.arange(17), freqs)
# 使用极坐标从freqs_for_each_token计算复数
freqs_cis = torch.polar(torch.ones_like(freqs_for_each_token), freqs_for_each_token)
# 通过频率旋转复数
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cis
q_per_token_as_complex_numbers_rotated.shape
# 输出: torch.Size([17, 64])获取旋转向量后,我们可以将其还原为原来的查询对,方法是再次将复数视为实数。
# 将旋转后的复数转换回实数
q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers_rotated)
# 打印结果张量的形状
q_per_token_split_into_pairs_rotated.shape
#### 输出 ####
torch.Size([17, 64, 2])
#### 输出 ####旋转后的配对现在已经合并,生成了一个新的查询向量(旋转查询向量),其形状为 [17x128],其中 17 是 token 的数量,128 是查询向量的维度。
# 将旋转后的token查询重塑为与原始形状匹配
q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape)
# 打印结果张量的形状
q_per_token_rotated.shape
#### 输出 ####
torch.Size([17, 128])
#### 输出 ####对于键,过程类似,但请记住键向量也是128维的。键的权重数量只有查询的1/4,因为它们在4个头之间共享以最小化计算。键也会被旋转以包含位置信息,类似于查询。
# 提取模型第一层注意力机制中的键权重张量
k_layer0 = model["layers.0.attention.wk.weight"]
# 重塑第一层注意力的键权重,以分离头
k_layer0 = k_layer0.view(n_kv_heads, k_layer0.shape[0] // n_kv_heads, dim)
# 打印重塑后的键权重张量的形状
k_layer0.shape # 输出: torch.Size([8, 128, 4096])
# 提取第一层注意力的第一头的键权重
k_layer0_head0 = k_layer0[0]
# 打印提取的第一头键权重张量的形状
k_layer0_head0.shape .shape # 输出: torch.Size([128, 4096])
# 通过矩阵乘法计算每个token的键
k_per_token = torch.matmul(token_embeddings, k_layer0_head0.T)
# 打印表示每个token键的张量的形状
k_per_token.shape # 输出: torch.Size([17, 128])
# 将每个token的键拆分成对并转换为浮点数
k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2)
# 打印拆分成对后的张量的形状
k_per_token_split_into_pairs.shape # 输出: torch.Size([17, 64, 2])
# 将每个token的键转换为复数
k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs)
# 打印表示每个token键的复数张量的形状
k_per_token_as_complex_numbers.shape # 输出: torch.Size([17, 64])
# 通过频率旋转复数键
k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis)
# 打印旋转后的复数键的形状
k_per_token_split_into_pairs_rotated.shape # 输出: torch.Size([17, 64, 2])
# 重塑旋转后的键以匹配原始形状
k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape)
# 打印旋转后的键的形状
k_per_token_rotated.shape # 输出: torch.Size([17, 128])我们现在为每个 token 都有了旋转后的查询和键,每个的大小为 [17x128]。
实现自注意力机制将查询矩阵和键矩阵相乘会给我们一个分数,这个分数将每个标记映射到另一个标记。这个分数表示每个标记的查询和键之间的关系。
# 计算每个 token 的 query-key 点积
qk_per_token = torch.matmul(q_per_token_rotated, k_per_token_rotated.T) / (head_dim) ** 0.5
# 打印表示每个 token 的 query-key 点积的张量的形状
qk_per_token.shape
#### 输出 ####
torch.Size([17, 17])
#### 输出 ####[17x17] 形状表示注意力得分(qk_per_token),其中 17 是提示中的 token 数量。
我们需要对查询-键得分进行屏蔽。在训练过程中,未来令牌的查询-键得分会被屏蔽,因为我们只使用过去的令牌来预测令牌。因此,在推理过程中,我们将未来令牌设置为零。
# 创建一个填充了负无穷值的掩码张量
mask = torch.full((len(tokens), len(tokens)), float("-inf"), device=tokens.device)
# 将掩码张量的上三角部分设置为负无穷
mask = torch.triu(mask, diagonal=1)
# 打印生成的掩码张量
mask
#### 输出 ####
tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
#### 输出 ####现在,我们需要对查询-键每令牌向量应用一个掩码。此外,我们还需要在其上应用softmax,将输出分数转换为概率。这有助于从模型的词汇表中选择最有可能的令牌或令牌序列,从而使模型的预测更加可解释,并适合诸如语言生成和分类等任务。
# 在每个 token 上将掩码添加到查询-键点积中
qk_per_token_after_masking = qk_per_token + mask
# 在掩码后沿第二维度应用 softmax
qk_per_token_after_masking_after_softmax = torch.nn.functional.softmax(qk_per_token_after_masking, dim=1).to(torch.bfloat16)对于值矩阵,它标志着自注意力部分的结束,类似于键,值权重也在每个4个注意力头之间共享以节省计算。因此,值权重矩阵的形状为[8x128x4096]。
# 获取注意力第一层的值权重
v_layer0 = model["layers.0.attention.wv.weight"]
# 将注意力第一层的值权重重塑为分离的头
v_layer0 = v_layer0.view(n_kv_heads, v_layer0.shape[0] // n_kv_heads, dim)
# 打印重塑后的值权重张量的形状
v_layer0.shape
#### 输出 ####
torch.Size([8, 128, 4096])
#### 输出 ####类似于查询和键矩阵,可以通过以下方式获取第一层和第一个头的值矩阵:
# 提取注意力第一层第一个头的价值权重值
v_layer0_head0 = v_layer0[0]
# 打印提取的价值权重张量的第一个头的形状
v_layer0_head0.shape
#### 输出 ####
torch.Size([128, 4096])
#### 输出 ####使用权重值,我们计算每个 token 的注意力值,从而得到一个大小为 [17x128] 的矩阵。这里,17 表示提示中的 token 数量,128 表示每个 token 的值向量维度。
# 通过矩阵乘法计算每个token的值
v_per_token = torch.matmul(token_embeddings, v_layer0_head0.T)
# 打印表示每个token值的张量的形状
v_per_token.shape
#### 输出 ####
torch.Size([17, 128])
#### 输出 ####为了获得最终的注意力矩阵,我们可以执行以下乘法:
# 通过矩阵乘法计算QKV注意力
qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token)
# 打印结果张量的形状
qkv_attention.shape
#### 输出 ####
torch.Size([17, 128])
#### 输出 ####我们现在有了第一层和第一个头的注意力值,换句话说就是自注意力的值。
实现多头注意力一个循环将被执行,为第一层中的每个头执行上述相同的计算。
# 将每个头的QKV注意力存储在一个列表中
qkv_attention_store = []
# 遍历每个头
for head in range(n_heads):
# 提取当前头的query、key和value权重
q_layer0_head = q_layer0[head]
k_layer0_head = k_layer0[head//4] # key权重在4个头之间共享
v_layer0_head = v_layer0[head//4] # value权重在4个头之间共享
# 通过矩阵乘法计算每个token的query
q_per_token = torch.matmul(token_embeddings, q_layer0_head.T)
# 通过矩阵乘法计算每个token的key
k_per_token = torch.matmul(token_embeddings, k_layer0_head.T)
# 通过矩阵乘法计算每个token的value
v_per_token = torch.matmul(token_embeddings, v_layer0_head.T)
# 将每个token的query拆分成对并旋转
q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2)
q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs)
q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers * freqs_cis[:len(tokens)])
q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape)
# 将每个token的key拆分成对并旋转
k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2)
k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs)
k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis[:len(tokens)])
k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape)
# 计算每个token的query-key点积
qk_per_token = torch.matmul(q_per_token_rotated, k_per_token_rotated.T) / (128) ** 0.5
# 创建一个填充为负无穷的掩码张量
mask = torch.full((len(tokens), len(tokens)), float("-inf"), device=tokens.device)
# 将掩码张量的上三角部分设置为负无穷
mask = torch.triu(mask, diagonal=1)
# 将掩码添加到每个token的query-key点积中
qk_per_token_after_masking = qk_per_token + mask
# 在掩码后沿第二个维度应用softmax
qk_per_token_after_masking_after_softmax = torch.nn.functional.softmax(qk_per_token_after_masking, dim=1).to(torch.bfloat16)
# 通过矩阵乘法计算QKV注意力
qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token)
# 存储当前头的QKV注意力
qkv_attention_store.append(qkv_attention)
# 打印存储的QKV注意力数量
len(qkv_attention_store)
#### 输出 ####
32
#### 输出 ####现在得到了第一层所有32个头的QKV注意力矩阵,所有的注意力得分将合并成一个大小为[17x4096]的大矩阵。
# 将所有头的QKV注意力沿最后一个维度拼接
stacked_qkv_attention = torch.cat(qkv_attention_store, dim=-1)
# 打印结果张量的形状
stacked_qkv_attention.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####层0注意力的最后一步是将权重矩阵与堆叠的QKV矩阵相乘。
# 通过与输出权重的矩阵乘法计算嵌入差值
embedding_delta = torch.matmul(stacked_qkv_attention, model["layers.0.attention.wo.weight"].T)
# 打印结果张量的形状
embedding_delta.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####我们现在有了注意力后的嵌入值变化,这些变化应该加到原始的 token 嵌入值上。
# 将嵌入增量添加到未归一化的标记嵌入中,以获得最终嵌入
embedding_after_edit = token_embeddings_unnormalized + embedding_delta
# 打印结果张量的形状
embedding_after_edit.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####嵌入变化经过归一化,然后通过前馈神经网络运行。
# 使用根均方归一化和提供的权重对编辑后的嵌入进行归一化
embedding_after_edit_normalized = rms_norm(embedding_after_edit, model["layers.0.ffn_norm.weight"])
# 打印归一化后的嵌入形状
embedding_after_edit_normalized.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####鉴于我们之前对 SwiGLU 激活函数的熟悉,我们将在这里应用之前研究过的方程。
SwiGLU: GLU 变体改进 Transformer (https://kikaben.com/swiglu-2020/)
# 获取前向层的权重
w1 = model["layers.0.feed_forward.w1.weight"]
w2 = model["layers.0.feed_forward.w2.weight"]
w3 = model["layers.0.feed_forward.w3.weight"]
# 执行前向层的操作
output_after_feedforward = torch.matmul(torch.functional.F.silu(torch.matmul(embedding_after_edit_normalized, w1.T)) * torch.matmul(embedding_after_edit_normalized, w3.T), w2.T)
# 打印前向层后的张量形状
output_after_feedforward.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####现在一切准备就绪,我们需要合并代码以生成31个更多的层。
# 使用未归一化的 token embeddings 初始化最终的 embedding
final_embedding = token_embeddings_unnormalized
# 遍历每一层
for layer in range(n_layers):
# 初始化一个列表来存储每一层每个 head 的 QKV 注意力
qkv_attention_store = []
# 使用当前层的权重对最终的 embedding 进行归一化
layer_embedding_norm = rms_norm(final_embedding, model[f"layers.{layer}.attention_norm.weight"])
# 获取当前层的注意力机制的 query、key、value 和 output 权重
q_layer = model[f"layers.{layer}.attention.wq.weight"]
q_layer = q_layer.view(n_heads, q_layer.shape[0] // n_heads, dim)
k_layer = model[f"layers.{layer}.attention.wk.weight"]
k_layer = k_layer.view(n_kv_heads, k_layer.shape[0] // n_kv_heads, dim)
v_layer = model[f"layers.{layer}.attention.wv.weight"]
v_layer = v_layer.view(n_kv_heads, v_layer.shape[0] // n_kv_heads, dim)
w_layer = model[f"layers.{layer}.attention.wo.weight"]
# 遍历每个 head
for head in range(n_heads):
# 提取当前 head 的 query、key 和 value 权重
q_layer_head = q_layer[head]
k_layer_head = k_layer[head//4] # key 权重在 4 个 head 之间共享
v_layer_head = v_layer[head//4] # value 权重在 4 个 head 之间共享
# 通过矩阵乘法计算每个 token 的 query
q_per_token = torch.matmul(layer_embedding_norm, q_layer_head.T)
# 通过矩阵乘法计算每个 token 的 key
k_per_token = torch.matmul(layer_embedding_norm, k_layer_head.T)
# 通过矩阵乘法计算每个 token 的 value
v_per_token = torch.matmul(layer_embedding_norm, v_layer_head.T)
# 将 query 按 token 分成对并旋转
q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2)
q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs)
q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers * freqs_cis)
q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape)
# 将 key 按 token 分成对并旋转
k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2)
k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs)
k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis)
k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape)
# 计算 query-key 的点积
qk_per_token = torch.matmul(q_per_token_rotated, k_per_token_rotated.T) / (128) ** 0.5
# 创建一个填充为负无穷的掩码张量
mask = torch.full((len(token_embeddings_unnormalized), len(token_embeddings_unnormalized)), float("-inf"))
# 将掩码张量的上三角部分填充为负无穷
mask = torch.triu(mask, diagonal=1)
# 将掩码添加到 query-key 的点积中
qk_per_token_after_masking = qk_per_token + mask
# 在掩码后沿第二维度应用 softmax
qk_per_token_after_masking_after_softmax = torch.nn.functional.softmax(qk_per_token_after_masking, dim=1).to(torch.bfloat16)
# 通过矩阵乘法计算 QKV 注意力
qkv_attention = torch.matmul(qk_per_token_after_masking_after_softmax, v_per_token)
# 存储当前 head 的 QKV 注意力
qkv_attention_store.append(qkv_attention)
# 将所有 head 的 QKV 注意力沿最后一个维度拼接
stacked_qkv_attention = torch.cat(qkv_attention_store, dim=-1)
# 通过矩阵乘法计算 embedding delta
embedding_delta = torch.matmul(stacked_qkv_attention, w_layer.T)
# 将 embedding delta 加到当前 embedding 上以获得编辑后的 embedding
embedding_after_edit = final_embedding + embedding_delta
# 使用当前层的权重对编辑后的 embedding 进行归一化
embedding_after_edit_normalized = rms_norm(embedding_after_edit, model[f"layers.{layer}.ffn_norm.weight"])
# 获取 feedforward 层的权重
w1 = model[f"layers.{layer}.feed_forward.w1.weight"]
w2 = model[f"layers.{layer}.feed_forward.w2.weight"]
w3 = model[f"layers.{layer}.feed_forward.w3.weight"]
# 对 feedforward 层进行操作
output_after_feedforward = torch.matmul(torch.functional.F.silu(torch.matmul(embedding_after_edit_normalized, w1.T)) * torch.matmul(embedding_after_edit_normalized, w3.T), w2.T)
# 使用编辑后的 embedding 加上 feedforward 层的输出更新最终的 embedding
final_embedding = embedding_after_edit + output_after_feedforward我们现在有了最终的嵌入表示,这是模型对下一个标记的猜测。它的形状与常规标记嵌入相同,为 [17x4096],包含17个标记,嵌入维度为4096。
# 使用根均方归一化(RMSNorm)和提供的权重对最终嵌入进行归一化
final_embedding = rms_norm(final_embedding, model["norm.weight"])
# 打印归一化后的最终嵌入的形状
final_embedding.shape
#### 输出 ####
torch.Size([17, 4096])
#### 输出 ####现在我们可以将嵌入解码为 token 值。
# 打印输出权重张量的形状
model["output.weight"].shape
#### 输出 ####
torch.Size([128256, 4096])
#### 输出 ####为了预测下一个值,我们利用最后一个 token 的嵌入。
# 通过最终嵌入与输出权重张量转置之间的矩阵乘法计算logits
logits = torch.matmul(final_embedding[-1], model["output.weight"].T)
# 打印结果logits张量的形状
logits.shape
#### 输出 ####
torch.Size([128256])
#### 输出 #### # 在最后一个维度上找到最大值的索引以确定下一个 token
next_token = torch.argmax(logits, dim=-1)
# 输出下一个 token 的索引
next_token
#### 输出 ####
tensor(2983)
#### 输出 ####获取由 token ID 生成的文本
# 使用tokenizer解码下一个token的索引
tokenizer.decode([next_token.item()])
#### 输出 ####
42
#### 输出 ####所以,我们的输入是“终极生命、宇宙和一切的问题的答案是”,输出是“42”,这是正确的答案。
你可以通过简单地更改整个代码中的这两行来尝试不同的输入文本,其余代码保持不变!
# 输入提示
prompt = "Your Input"
# 用输入中的总token数替换17这个数字
# 可以使用len(tokens)来检查总token数
freqs_for_each_token = torch.outer(torch.arange(17), freqs)共同学习,写下你的评论
评论加载中...
作者其他优质文章