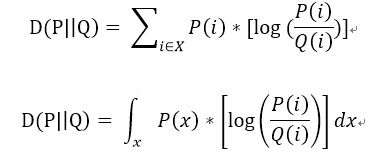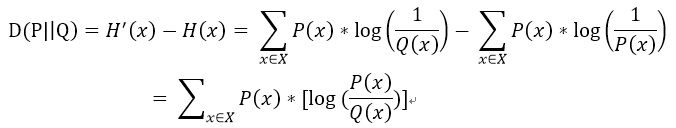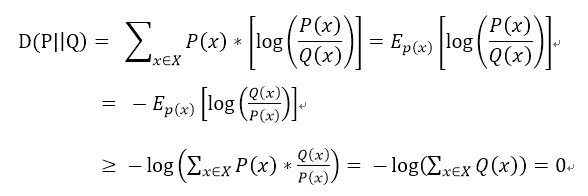在概率论或信息论中,KL散度( Kullback–Leibler divergence),又称相对熵(relative entropy),是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P的拟合分布。有人将KL散度称为KL距离,但事实上,KL散度并不满足距离的概念,应为:1)KL散度不是对称的;2)KL散度不满足三角不等式。对一个离散随机变量或连续的随机变量的两个概率分布P和Q来说,KL散度的定义分别如下所示。
KL散度在信息论中有自己明确的物理意义,它是用来度量使用基于Q分布的编码来编码来自P分布的样本平均所需的额外的Bit个数。而其在机器学习领域的物理意义则是用来度量两个函数的相似程度或者相近程度,在泛函分析中也被频繁地用到[2]。在香农信息论中,用基于P的编码去编码来自P的样本,其最优编码平均所需要的比特个数(即这个字符集的熵)为:
用基于P的编码去编码来自Q的样本,则所需要的比特个数变为:
于是,我们即可得出P与Q的KL散度
可以利用Jensen不等式证明P与Q之间的KL散度不小于0:
参考资料:[1] KL散度的解释,https://baike.so.com/doc/4949446-5170752.html.
[2] KL散度与Jensen不等式的理解,https://zhuanlan.zhihu.com/p/28249050.
共同学习,写下你的评论
评论加载中...
作者其他优质文章