首页手记【九月打卡】第20天 Python3入门机器学习

【九月打卡】第20天 Python3入门机器学习

标签：

Python 机器学习

①课程介绍

课程名称：Python3入门机器学习经典算法与应用入行人工智能
课程章节：10-1；10-2
主讲老师：liuyubobobo

内容导读

第一部分 SVM介绍
第二部分 SVM实现

②课程详细

第一部分 SVM介绍

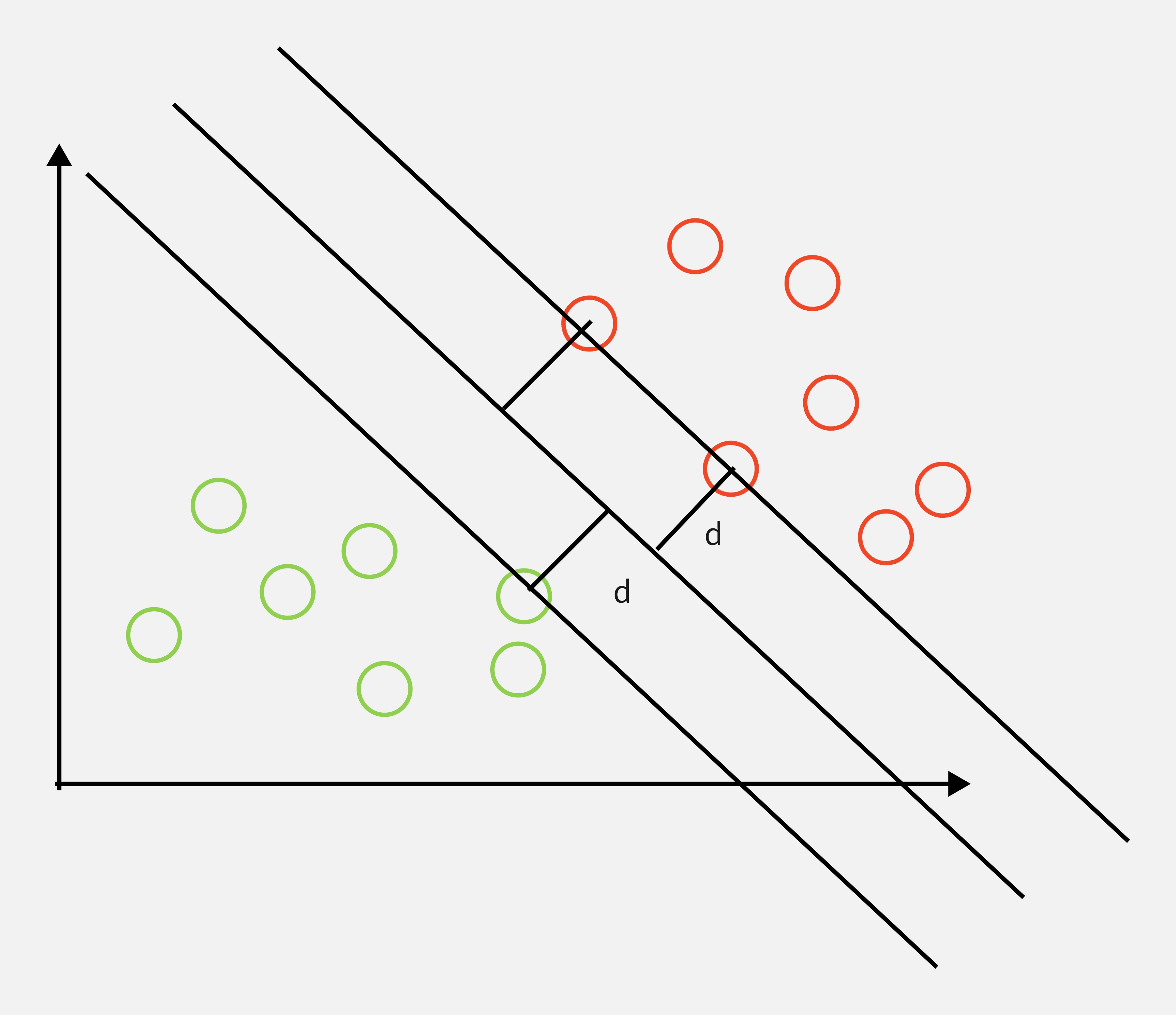
对于 SVM 而言，就是要找到中间的那根线，他相当于是那个最优的决策边界，这个决策边界距离两个类别的最近样本最远。对于这些最近的样本，被称为“支撑向量”。界定这个区域的两根直线的距离，通常我们称为是“margin”。SVM 要做的事情就是最大化 margin。这样的话，我们要解决的便是一个最优值求解的问题。

另外值得一提的是，SVM对异常点很敏感，

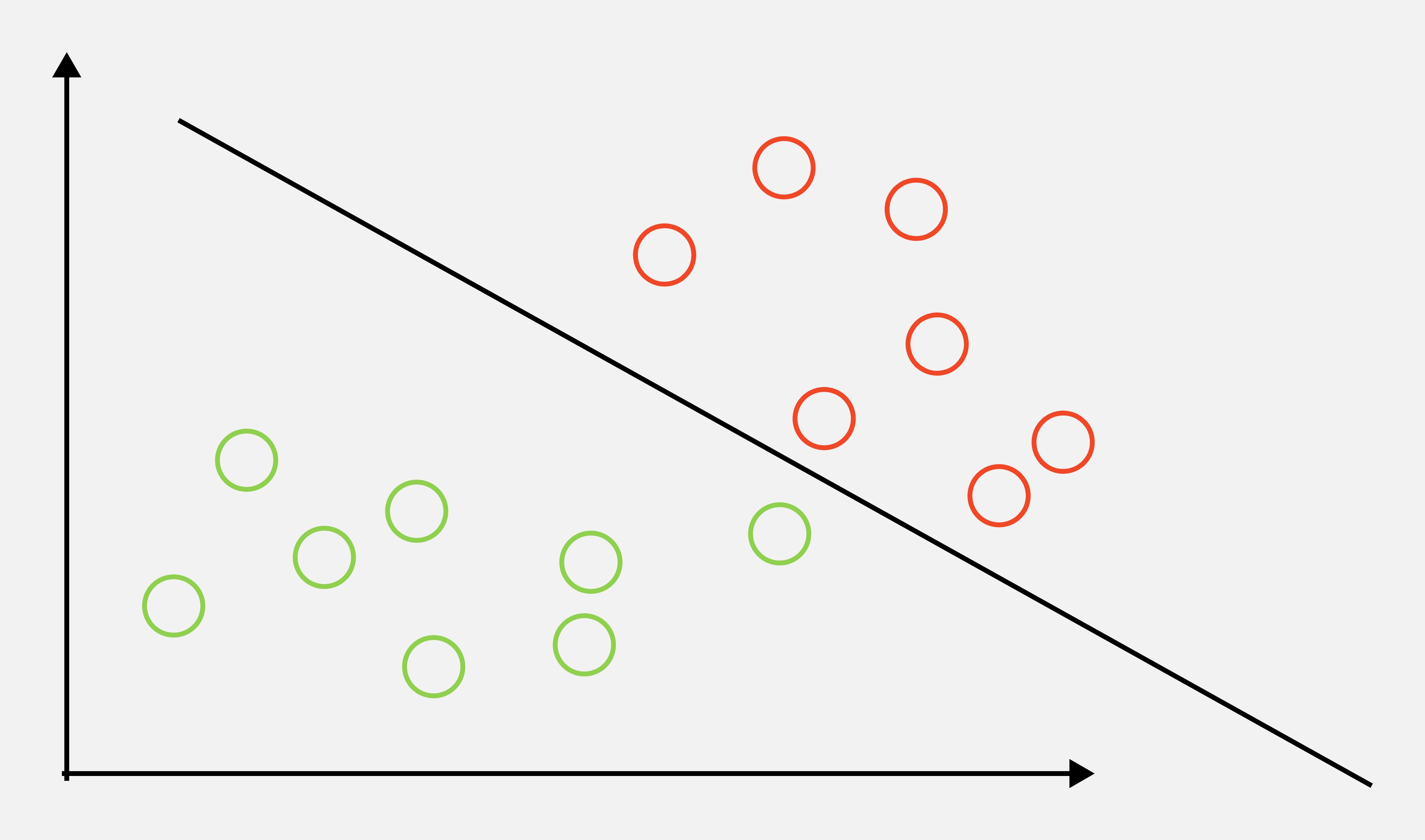
比如加入一个异常点

不看上面的图1直接看图2，其实这样SVM找的决策边界还是很合理的，不过这是数据量小的情况，假设左边7个绿色的球是700个，7个红色球是700个，只因为1个异常数据点的影响就极大地改变了决策图像，影响了后续泛化能力，
后面介绍的soft margin 将缓解这个问题

第二部分 SVM实现

导入函数

import numpy as np
import matplotlib.pyplot as plt

导入数据

from sklearn import datasets

iris = datasets.load_iris()

X = iris.data
y = iris.target.copy()

X = X[y<2,:2]
y = y[y<2]

对数据进行降维处理进行可视化，以便于分析数据结构

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
pca.fit(X)
X_redection = pca.transform(X)

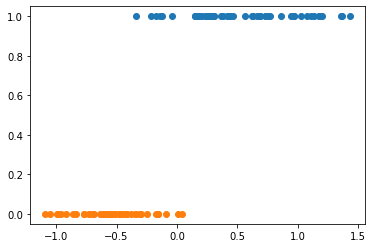
一维可视化数据

plt.scatter(X_redection[y==1], y[y==1])
plt.scatter(X_redection[y==0], y[y==0])
plt.show()

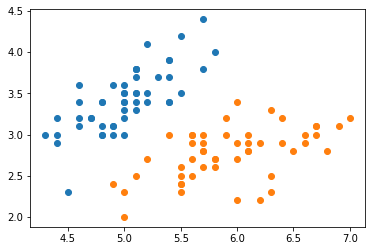
二维可视化

plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

数据很清爽
对数据进行归一化

from sklearn.preprocessing import StandardScaler

standardscaler = StandardScaler()
standardscaler.fit(X)
X_standard = standardscaler.transform(X)

调用线性SVM算法

from sklearn.svm import LinearSVC

svc = LinearSVC(C=1e9)
svc.fit(X_standard, y)

定义决策边界的函数

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

可视化SVM分类之后的决策边界

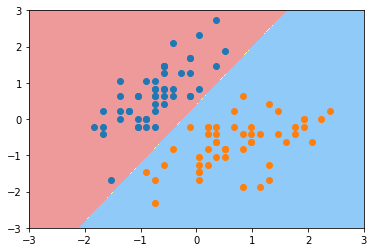
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

可以发现这个决策边界应为左下角的异常点影响导致决策边界产生了偏斜，我们可以通过调解C的值来变形

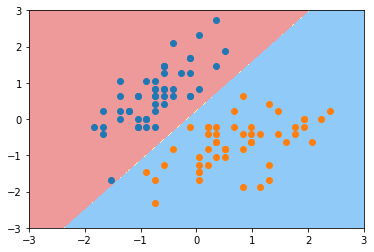
svc2 = LinearSVC(C=1)
svc2.fit(X_standard, y)
plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

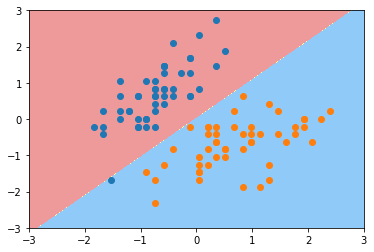
svc3 = LinearSVC(C=0.01)
svc3.fit(X_standard, y)
plot_decision_boundary(svc3, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

通过对C的调整能一定程度排除异常点的干扰