【九月打卡】第14天 算法设计思想之“动态规划”
标签:
JavaScript
课程名称:JavaScript版数据结构与算法
课程章节:第13章 算法设计思想之“动态规划”
主讲老师:lewis
课程内容:
今天学习的内容包括:
13-1 动态规划简介——解决子问题相互重叠的问题。
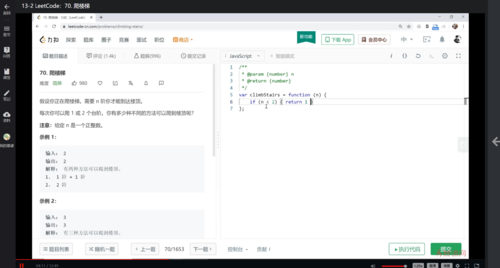
13-2 LeetCode:70. 爬楼梯——使用动态规划的f(n)=f(n-1)+f(n-2)计算有多少种方法。
课程收获:
动态规划
动态规划是什么
- 动态规划是算法设计中的一种方法。
- 它将一个问题分解为相互重叠的子问题,通过反复求解子问题,来解决原来的问题。
应用场景:斐波那契数列
- 定义子问题:F(n) = F(n-1) + F(n-2)。
- 反复执行:从2循环到n,执行上述公式。
动态规划 vs 分而治之
- 子问题是否相互独立。
70. 爬楼梯
解题思路
- 爬到第n阶可以在第n-1阶爬1个台阶,或者在第n-2阶爬2个台阶。
- F(n) = F(n-1) + F(n-2)。
- 使用动态规划。
解题步骤
- 定义子问题:F(n) = F(n-1) + F(n-2)。
- 反复执行:从2循环到n,执行上述公式。
for (let i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
性能分析
- 时间复杂度:O(n)。
- 空间复杂度:O(n) or O(1)。
今天 通过 动态规划 学习了 爬楼梯有多少种方法的算法题,因为前端是重时间轻空间的,所以空间复杂度O(n)是可以接受的。一共学习了两种方法,对自己的思维有着一定的触发,对自己说一句,加油😀~
坚持打卡,坚持学习!明天见💪~
点击查看更多内容
为 TA 点赞
评论
共同学习,写下你的评论
评论加载中...
作者其他优质文章
正在加载中
感谢您的支持,我会继续努力的~
扫码打赏,你说多少就多少
赞赏金额会直接到老师账户
支付方式
打开微信扫一扫,即可进行扫码打赏哦