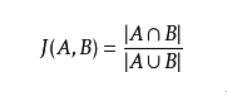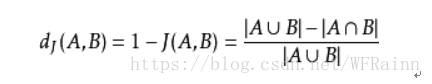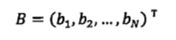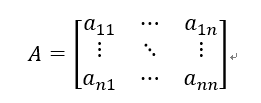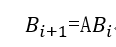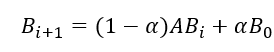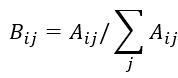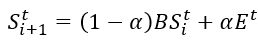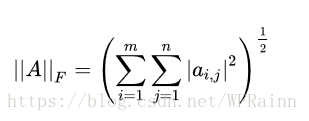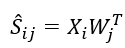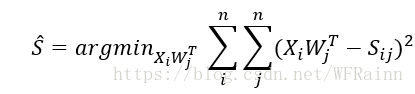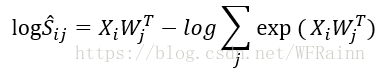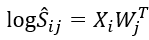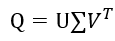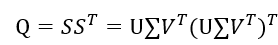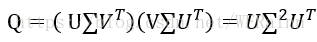近日，因为一些奇妙的原因，拜读了《A networkIntegration Approach for Drug-Target interaction Prediction and ComputationalDrug Repositioning from Heterogeneous Information》这篇文章。花了将近一周的时间终于算是大概弄懂了其主要算法的原理，恰逢正在学习python，便着手将提供的matlab代码改成了python，便想阐述一下我对这篇文章的理解与其python的实现与在这个过程中遇到的问题，作为自己学习的记录吧。

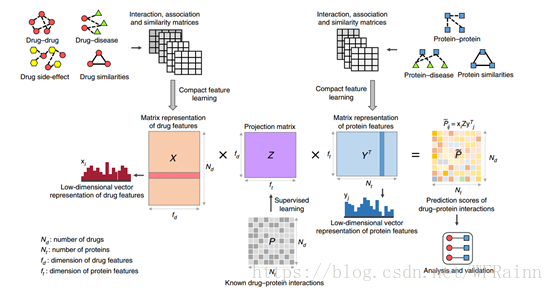
这篇文章的主要目的在于通过各种与蛋白和药物相关的数据，对药物靶点进行预测，包括了药物与药物的作用，药物与疾病的作用，药物与side-effect的作用，蛋白与蛋白的作用，蛋白与疾病的作用，药物与蛋白本身的相似性以及药物与蛋白的相互作用。因为我是先拿到这个题目之后才了解到这篇文章，在刚拿到这个题目的时候，我的想法是直接用蛋白与药物本身的相似性通过interaction直接学习不就好了吗，为什么还要给有关疾病、side-effect的数据呢。看完文章后才了解到他是通过将药物、蛋白与其它相关数据转换成药物与蛋白本身的相似性，从而使得最后的相似性矩阵可以包含更多的信息，从而提高预测的准确率。

DTINet实现所基于的假设为“guilt byassociation”，即两种药物或两种蛋白，其相似度越高，则其更有可能具有类似的作用，换一句话说，两个节点的拓扑结构越相似，其功能也越相似。通过将原始数据进行处理加工，最终转换成药物与蛋白的拓扑结构，然后通过已知的药物与蛋白的相互作用，便可学习得到药物与蛋白相互作用的模型，从而可以预测药物于蛋白之间新的相互作用。DTINet主要的步骤如下：

1.compute similarity

第一步需要将原始数据转化为similarity matrices，这里用到的是杰卡德相似指数(Jaccardsimilarity coefficient)。

杰卡德相似系数(Jaccard similarity coefficient)，也称杰卡德指数(JaccardIndex)，是用来衡量两个集合相似度的一种指标。而杰卡德距离（Jaccard distance）是用来衡量两个集合差异性的一种指标，它是杰卡德相似系数的补集，被定义为1减去Jaccard相似系数。

Jaccard相似指数被定义为两个集合交集的元素个数除以并集的元素个数：

Jaccard距离即为：

Jaccard距离只适用于0-1矩阵，同时，其与汉明距离（Hamming distance）的区别为，Hamming距离关注0-0匹配，而Jaccard距离在计算时去除了0-0匹配，这也是为什么算法使用Jaccard距离而不是Hamming距离，例如两种药物都无法产生某种side-effect，但这并不一定代表其存在相似的信息。

在这里运用时是计算矩阵中每一行向量的Jaccard相似度，并转化为相似度矩阵，类似于相关系数矩阵，是一个对称矩阵。其python代码实现如下：

import pandas as pd
import numpy as np
from scipy.spatial.distance import pdist
from scipy.spatial.distance import squareform
import utils

Nets = ['mat_drug_drug', 'mat_drug_disease', 'mat_drug_se','mat_protein_protein', 'mat_protein_disease']

for net in Nets:
    inputID='./data/'+net+'.txt'
    M=pd.read_table(inputID,sep=' ', header=None)
    # jaccard similarity
    Sim=1-pdist(M,'jaccard')
    Sim=squareform(Sim)
    Sim=Sim+np.eye(len(Sim))
    Sim=np.nan_to_num(Sim)
    
    #output csv file
    outputID='./data/Sim_'+net+'.csv'
    utils.outputCSVfile(outputID,Sim)
    
#write chemical similarity to networks
M=pd.read_table('./data/Similarity_Matrix_Drugs.txt',sep='    ',header=None)
M=M.as_matrix(columns=None)
utils.outputCSVfile('./data/Sim_mat_drugs.csv',M)
#write sequence similarity to networks
M=pd.read_table('./data/Similarity_Matrix_Proteins.txt',sep=' ',header=None)
M=M.as_matrix(columns=None)
M=M/100
utils.outputCSVfile('./data/Sim_mat_proteins.csv',M)

其中outputCSVfile为：

import csv
import pandas as pd
def outputCSVfile(filename,data):
    csvfile=open(filename,'wb')
    writer=csv.writer(csvfile)
    writer.writerows(data)
    csvfile.close()

其中pdist函数的文档如下：

其return的为一个1×n的向量，需要使用squarefrom()转化回矩阵

[python] view plain copy print?

另外药物与蛋白本身的相似度矩阵并不需要转化，可以直接使用。这样我们就得到了drug_drug,drug_disease,drug_side-effect,protein_protein,protein_disease,drug,protein,7个相似度矩阵，接着我们就可以进行下一步了。

2.compact featurelearning

现在我们已经得到了7个相似度矩阵，但是如果直接进行分析学习，每个矩阵都是成百上千维，计算量太过庞大，同时还会有很多噪声，这时便需要降维，也就是compact整个数据集。

在文章中作者分了两步进行降维，首先使用重启随机游走算法得到相关度评分矩阵，接着通过奇异值分解与矩阵分解得到降维后的向量。

2.1 random walkwith restart

说实话我现在也不是很懂为什么要使用重启随机游走算法，因为在我看来直接使用得到的相似度矩阵进行主成分分析（PCA）不就可以降维了吗。查阅网上的资料大概解释是使用重启随机游走算法可以获得更多网络拓扑结构的信息。我的理解是我们得到的相似度矩阵只是孤立的计算了两个节点间的相似度，但是没有考虑更多节点间的相互联系。很抽象，只能理解个大概。

下面就来介绍一下重启随机游走算法（random walk with restart）。它的前身是pagerank算法，pagerank算法是google的网页排名算法由拉里佩奇发明，其基本思想是民主表决。在互联网上，如果一个网页被很多其他网页所链接，说明它受到普遍的承认和信赖，那么它的排名就高。同时，排名高的网站链接可靠，所以这些链接的权重会更大。

其计算方法为：

设N个网页的排名为向量B

其中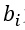为第i个网页的网页排名。设矩阵A

其中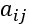为第i个网页转移到第j个网页的概率，易得每一列的和为1

那么，假设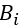是第i次迭代的结果，

由此进行迭代，最终B将收敛于排名的真实值，至于收敛性的证明，有点复杂，就不阐述了，这篇文章中已较好的阐述了：

PageRank算法--从原理到实现

而重启随机游走算法，就是在pagerank的基础上加上了一个跳转至随机网页的概率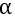，也就是重启，以此解决终止点与陷阱的缺陷（可见浅谈PageRank

），由此，迭代公式变成了

最终，经过迭代到达平稳，平稳后得到的概率分布可被看作是受开始节点影响的分布。重启随机游走可以捕捉两个节点之间多方面的关系，捕捉图的整体结构信息。

重启随机游走算法（RWR）

那么，在此处，我们现在已知节点间相似度矩阵A，如果定义两个节点间相似度越大，其发生相互跳转的概率越大，这样我们便可以得到转移概率矩阵B,其中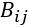为：

接下来便进行迭代收敛得到最终的得分矩阵

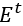
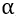
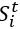
其中为n维的单位向量，为重启概率。最终得到的得分矩阵也称为节点的diffusion state，若两个节点间的diffusion state相似，则其在网络中有着更加相似的位置。

Python代码实现如下

import numpy as np
import pandas as pd

def diffusionRWR(A,maxiter,restartProb,netname):
    n=len(A)
    #normalize the adjacency matrix
    P=A/A.sum(axis=0)
    
    #Personalized PageRank
    restart=np.eye(n)
    Q=np.eye(n)
    for i in range(1,maxiter):
        Q_new=(1-restartProb)*np.dot(P,Q)+restart*restartProb
        delta=np.linalg.norm((Q-Q_new))
        print 'this is'+netname + str(i)+ ' circulation,the delta='+str(delta)
        Q=Q_new
        if delta<1e-6:
            break
    return Q

1.其中A.sum(axis=0)计算的是矩阵每一列的和，如果axis=1则为每一行的和

2.np.linalg.norm()计算的是frobenius范数，可用来表示误差，其定义为：

2.2SVD与矩阵分解

在使用RWR得到了各个节点的diffusion state之后，便可以进行数据降维了，一般来说数据降维常用的就是SVD分解，作者在这里也是使用了这个思想，但是作者引入了一个奇妙的思想，将diffusionstate看作两种feature结合作用而得到的，一种为nodefeature， 定义为X，另一种是context feature，定义为W，则

那么，我们便可以构造目标函数来逼近S：

对于这个函数，作者使用了SVD分解的方法进行求解，由定义可知

其中第二项为对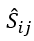的归一化约束，可忽略，于是变为：

于是可以看成是两个矩阵相乘得到的S，那么如果我们反向对log(S)进行SVD分解便可以得到分解后的两个矩阵。为了避免log(0)，每个元素加上一个很小的数α=1/n

利用SVD进行分解：

对于SVD奇异值分解，这里有几篇文章：

机器学习系列-SVD篇

奇异值的物理意义是什么？

然后，我们取前d个奇异值和奇异向量，于是

X代表node feature矩阵，W代表context feature矩阵。

在实际处理时，由于我们有多个diffusion state矩阵，可以先将矩阵进行拼接，得到矩阵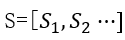，同时，对于矩阵

由于U和V都是酉矩阵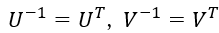，，则

上式称为矩阵Q的特征值分解，这样，如果我们要对S进行奇异值分解，只需要对Q进行特征值分解。

于是

其中，为对Q进行特征值分解得到的特征值矩阵取前d个特征值。

这样，我们便可以得到降维后的node feature矩阵，维数为n×d。

其python实现如下：

from __future__ import division
import numpy as np
import pandas as pd
import diffusionRWR as RWR
import math
import scipy.linalg as la
import utils
def DCA(networks,dim,rsp,maxiter):
    i=1
    P=np.array([])
    for network in networks:
        fileID='./data/'+network+'.csv'
        net=pd.read_csv(fileID,header=None)
        net=net.as_matrix(columns=None)
        tQ=RWR.diffusionRWR(net,maxiter,rsp,network)
        if i==1:
            P=tQ
        else:
            #concatenate network
            P=np.hstack((P,tQ))
        i+=1
    print P.shape
    nnode=len(P)
    alpha=1/nnode
    P=np.log(P+alpha)-math.log(alpha)
    P=np.dot(P,P.T)
    
    #use SVD to decompose matrix
    U,Sigma,VT=la.svd(P,lapack_driver='gesvd',full_matrices=True)
    sigd=np.dot(np.eye(dim),np.diag(Sigma[:dim]))
    Ud=U[:,:dim]
    #get context-feature matrix, since we use P*PT to get square matrix, we need to sqrt twice
    X=np.dot(Ud,np.sqrt(np.sqrt(sigd)))
    return X,P,U,np.sqrt(np.sqrt(sigd))


maxiter = 20
restartProb = 0.50
dim_drug = 100
dim_prot = 400
drugNets = ['Sim_mat_drug_drug', 'Sim_mat_drug_disease', 'Sim_mat_drug_se', 'Sim_mat_Drugs']
proteinNets = ['Sim_mat_protein_protein', 'Sim_mat_protein_disease', 'Sim_mat_Proteins']
Y=DCA(proteinNets,dim_prot,restartProb,maxiter)
X=DCA(drugNets,dim_drug,restartProb,maxiter)
X=np.array(X)
Y=np.array(Y)
utils.outputCSVfile('./data/drug_vector_d.csv',X)
utils.outputCSVfile('./data/protein_vector_d.csv',Y)

1.其中np.hstack()为矩阵拼接函数，将新矩阵拼接在右边，需要保证两个矩阵的行数一致，如果需要在下方拼接，可用np.vstack()。

2.len(P)为计算矩阵行数，计算列数可用len(P.T)

3.np.diag()可将向量转化为对角矩阵。

得到了drug-feature和protein-feature矩阵后，我们便可以开始预测drug和protein的相互作用了。论文中使用的是inductive matrix completion进行监督学习，虽然imc可能不是这篇文章的重点，但是imc对现在的我来说大概是最难懂的部分了，看了很多文献也还没有弄明白，在论文中提供的代码imc部分是用c++写的并且被封装了，也无法看到代码，所以待我看懂后再写吧哈哈。

另外代码已经上传至github：https://github.com/JiaruiFeng/DTINet-with-python

此篇文章仅作为学习记录，如有任何侵权问题，请发消息给我，我将立马删除。

citations：

[1]Luo Y, Zhao X, Zhou J, et al. A Network Integration Approach for Drug-Target Interaction Prediction and Computational Drug Repositioning from Heterogeneous Information[J]. bioRxiv, 2017: 100305.

[2]Tong, Faloutsos, Christos, et al. Random walk with restart: fast solutions and applications[J]. Knowledge & Information Systems, 2008, 14(3):327-346.

[3]随机游走与网络分析

原文出处