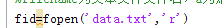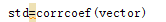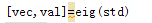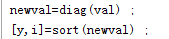主成分分析方法

一、是什么：

因为在研究问题的时候，有时候影响一个事物的因素有很多（就是一个y对应很多自变量）而自变量之间又有相关关系（说明自变量在某种程度上可以相互替换）。实现一种正交变换（不相关就叫正交），从而将高维系统表示为低维系统，

为了简化（将很多自变量变成很少自变量）而提出的一种方法。

比如：遥感中，多波段的信息，通过主成分分析方法，最终转化为前3个波段就可能包含了95%以上的信息。主成分分析的结果可以用于回归分析、聚类分析、神经网络分析

实践：利用matlab自己编程完成主成分分析

1.打开数据（txt）

fid=fopen(filename)返回一个文件代码

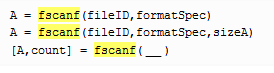
2.读取数据从(txt)

fscanf(fid,'%g'，[a b])

3.调用一个std函数（总和标准化法标准化矩阵：每个值除以自己所在列的求和）返回一个标准化的矩阵

4.最重要的一步

1.计算相关系数矩阵（利用corrcoef()函数输入一个矩阵（就是刚刚标准化过的矩阵）返回一个相关系数矩阵）

2.计算特征向量和特征值：（返回多个变量时需要用方括号括起来）

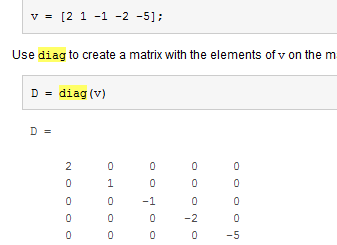
3.对特征值排序：diag函数的运用

4.计算贡献率：（大于85的放进一个新的）

5.计算载荷

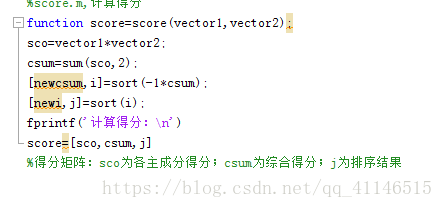
5.计算得分

原文出处