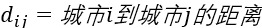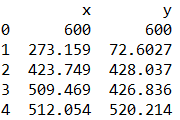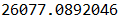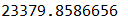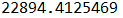模拟退火算法与其python实现（二）——TSP问题

上一篇文章介绍了模拟退火算法的基本原理（模拟退火算法与其python实现(一)），这篇文章介绍一下模拟退火算法在数学建模中最常应用的一类问题——Traveling salesman problem,也就是旅行商问题，这类问题的描述如下：

一个旅行商从城市1 出发，需要到其它城市n去推销货物，最后返回城市1 。若任意两个城市间的距离已知，旅行商如何选择最佳行走路线？

这种问题也就是上篇提到的NP-hard问题中很典型的一类，如果使用枚举法，随着城市数目的增多，计算量将几何倍数的递增。那么，如何使用SA算法来求近似最优解呢，首先我们这个问题转化为数学模型：

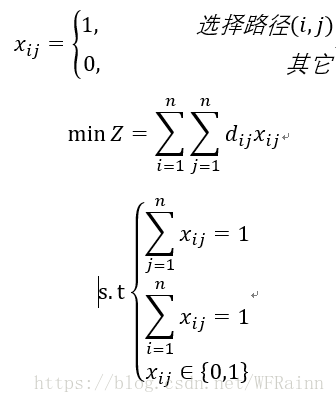
设

我们所求即为函数Z的最小值，下面我们便使用python来构建TSP问题的SA模型并尝试求得近似最优解

首先导入问题数据并处理：

from __future__ import division
import pandas as pd
import utils
import numpy as np
import math
import matplotlib.pyplot as plt
citys=pd.read_table('./data/tsp100.txt',sep='\t',header=None)
citys.columns=['x']
citys['y']=None

for i in range(len(citys)):
    coordinate=citys['x'][i].split()
    citys['x'][i]=float(coordinate[0])
    citys['y'][i]=float(coordinate[1])

print citys.head(5)

其中:

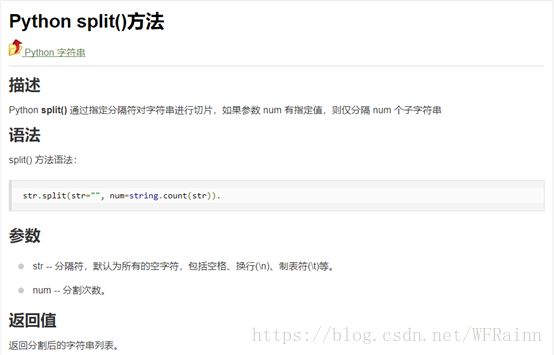
1.string.split()可以剪切字符串，其用法如下：

接着看下数据长什么样

数据集存储了各个城市的坐标，我们把第一个城市作为我们的起点，同时也是我们的终点。接着在数据集中除去这个城市以便于计算。

start=list(citys.iloc[0])
end=list(citys.iloc[0])
citys=citys.drop([0])
citys.index=[i for i in range(len(citys))]

接着我们便可以初始化我们的行走路线了，我们直接将数据集中城市存储的顺序做为我们最初的行走路线

paths=[i for i in range(len(citys))]# initiate path

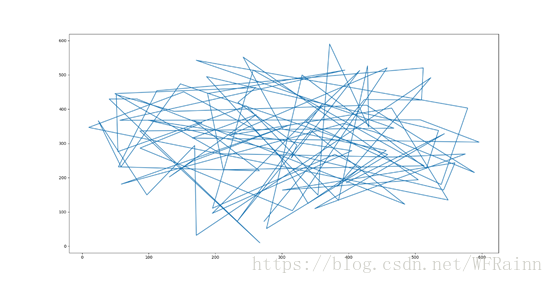
通过matplotlib可以得到初始路径的路线图：

然后我们按照在上文提到的规则设置初始温度，即随机选择几组状态，计算能量差值最大的一组，以此为依据得到初始温度，我们设接受概率为0.5。

'''
random path and calculate distance to sreach for optimal initiate temperature
'''

distance1=0
distance2=0
dif=0
for i in range(10):  
    #np.random.shuffle(path)
    newPaths1=list(np.random.permutation(paths))
    newPaths2=list(np.random.permutation(paths))
    distance1=utils.CalLength(citys,newPaths1,start,end)
    distance2=utils.CalLength(citys,newPaths2,start,end)
    difNew=abs(distance1-distance2)
    if difNew>=dif:
        dif=difNew

Pr=0.5 #initiate accept possibility
T0=dif/Pr#initiate terperature

1.其中计算距离的函数定义在utils模块中：

import math
def CalDistance(x,y):
    return math.sqrt(x**2+y**2)

def CalLength(citys, paths,start,end):
    length=0
    n=1
    for i in range(len(paths)):
        if i==0:
            length+=CalDistance(start[0]-citys['x'][paths[i]],start[1]-citys['y'][paths[i]])
            n+=1
        elif n<len(paths):
            length+=CalDistance(citys['x'][paths[i]]-citys['x'][paths[i+1]],citys['y'][paths[i]]-citys['y'][paths[i+1]])
            n+=1
        else:
            length+=CalDistance(citys['x'][paths[i]]-end[0],citys['y'][paths[i]]-end[1])
    return length

2.np.random.permutation(list)可以打乱数据在list中的排序，但不会直接替换原list,而np.random.shuffle(list)会直接替换。

现在我们可以初始化其它参数：

T=T0
Tmin=T/50
k=10*len(paths) #times of internal circulation 
length=0#initiate distance according to the initiate path
length=utils.CalLength(citys,paths,start,end)
print length
t=0 #time

计算得到初始路径所需要走的距离为：

然后执行降温过程，这里，关于邻域函数的设置，我们首先设置为调换路径中某对节点的位置。

while T>Tmin:
    for i in range(k):
        a=0
        b=0
        newPaths=paths
        while a==b:
            a=np.random.randint(0,len(paths))
            b=np.random.randint(0,len(paths))
        te=newPaths[a]
        newPaths[a]=newPaths[b]
        newPaths[b]=te
        newLength=utils.CalLength(citys,newPaths,start,end)
        if newLength<length:
            length=newLength
        else:
             #metropolis principle
             p=math.exp(-(newLength-length)/T)
             r=np.random.uniform(low=0,high=1)
             if r<p:
                 length=newLength
    t+=1
    print t
    T=T0/(1+t)
print length

最后执行结果如下

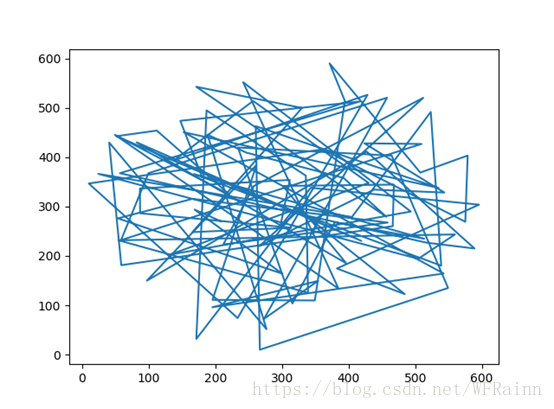
路径图为下：

现在我们尝试一下改进SA算法：

首先，我们更改初始路径，使初始路径也随机生成：

paths=list(np.random.permutation(paths))

接着，我们改进一下邻域函数，将函数设置为根据温度的大小，调换多对节点的位置，这样，能够增加遍历整体的概率。

for j in range(int(T0/500)):
    a=0
    b=0
    while a==b:
        a=np.random.randint(0,len(paths))
        b=np.random.randint(0,len(paths))
    te=newPaths[a]
    newPaths[a]=newPaths[b]
    newPaths[b]=te
newLength=utils.CalLength(citys,newPaths,start,end)

接着我们可以设置一个增温过程，即有一定概率重新升温，以避免算法在局部最小值处停滞不前。我们设置重升温的概率为0.15。

back=np.random.uniform(low=0,high=1)
if back>=0.85:
    T=T*2
    continue

最终，我们SA模型如下：

paths=list(np.random.permutation(paths))
while T>Tmin:
    for i in range(k):
        newPaths=paths
        for j in range(int(T0/500)):
            a=0
            b=0
            while a==b:
                a=np.random.randint(0,len(paths))
                b=np.random.randint(0,len(paths))
            te=newPaths[a]
            newPaths[a]=newPaths[b]
            newPaths[b]=te
        newLength=utils.CalLength(citys,newPaths,start,end)
        if newLength<length:
            length=newLength
        else:
             #metropolis principle
             p=math.exp(-(newLength-length)/T)
             r=np.random.uniform(low=0,high=1)
             if r<p:
                 length=newLength

    back=np.random.uniform(low=0,high=1)
    if back>=0.85:
        T=T*2
        continue
    t+=1
    print t
    T=T0/(1+t)
print length

执行算法，得到结果：

代码与数据已上传至github：https://github.com/JiaruiFeng/Simulated-Annealing-solving-TSP-with-python

原文出处