LeetCode 盛最多水的容器

盛最多水的容器

题目来源：https://leetcode-cn.com/problems/container-with-most-water/

题目

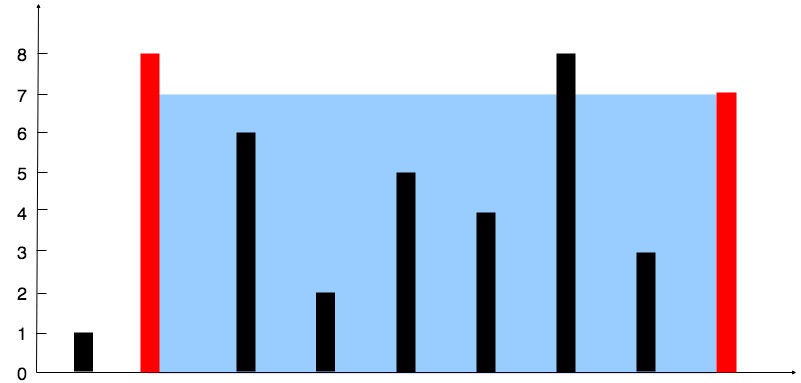
给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

解题思路

1. 采用双指针的方法；
2. 定义最大值 max_area 用以比较确定最终最大值。定义双指针，一个指向开始，一个指向末尾；
3. 双指针向两边靠拢，靠拢的准则：指针指向的线较短部分往较长的线那边移动。具体的原因是：距离确定，最终盛放的容量大小由较短的线决定，若往较长线移动，移动后指针指向的线若变长，虽然距离变短，当仍有可能与距离乘积比前面定义的 max_area 的值大（也就是盛放的容量变大）；
4. 两个指针重合退出循环，返回最终确定的最大值 max_area。

代码实现

class Solution:
    def maxArea(self, height: List[int]) -> int:
        # 定义最大值，用以后续比较
        # 定义双指针，一个指向开始，一个指向末尾
        max_area, l, r = 0, 0, len(height) - 1
        # 双指针向中间靠拢
        while l < r:
            # 以较短的线为准，与两线之间的距离之积就是可盛放水量的值
            # 与定义的最大值 max_area 比较，取大值重新赋值给 max_area
            max_area = max(max_area, min(height[l], height[r]) * (r - l))
            # 每次移动的准则：较短的线往较长线的靠拢
            # 具体原因：往较长线移动，移动后的线若变长，虽然距离变短，当仍有可能与距离乘积变大（也就是盛放的容量变大）
            if height[l] < height[r]:
                l += 1
            else:
                r -= 1
        return max_area

实现结果

以上就是本篇的主要内容

欢迎关注微信公众号《书所集录》