八月的一个清晨,数学天才、菲尔兹奖得主陶哲轩点开了一封来自三位陌生物理学家的邮件。
三人在邮件中解释道:
我们偶然发现了一个公式,如果这个公式是正确的,那么它就会在线性代数中一些最基本且重要的对象之间建立一种意想不到的关系。
然而陶哲轩的第一反应却是:
这么短、这么简单的东西,早就应该出现在教科书里了。这不可能是真的。
其实,陶哲轩向来不喜欢以这种方式被咨询,甚至在他的主页上写下了警告:别拿你的手稿随便打扰我。
但令三位物理学家惊讶的是,仅仅2个小时之后,他们就收到了陶哲轩的回复。
而更意想不到的是,在一周半后,他们还一起发表了论文,阐述了这个公式的证明过程。
是什么样的公式受到陶哲轩如此青睐?
求解特征向量。
没错,就是这个再普通不过的基础数学求解公式。
按照传统解法:
计算特征多项式→求解特征值→求解齐次线性方程组,得出特征向量。
而这三位物理学家在研究“中微子”的过程中,却意外发现另一种奇妙解法:
知道特征值,只需要列一个简单的方程式,特征向量便可迎刃而解。
△三位物理学家。从左至右:张西宁、Peter Denton和Stephen Parke。
就像陶哲轩所说:
这个公式看起来好得令人难以置信。
我完全没想过,子矩阵的特征值编码了原矩阵特征向量的隐藏信息。
耶鲁大学数学家Van Vu则用“惊人”和“有趣”两个词来形容这一发现。
一位Hacker News网友甚至认为,这一公式的理论价值在克莱姆法则之上。
注:克莱姆法则是线性代数中的基本定理,用行列式计算出n元一次方程组的解。
新方法怎么来的?
先来回顾下我们所熟知的特征向量和特征值。
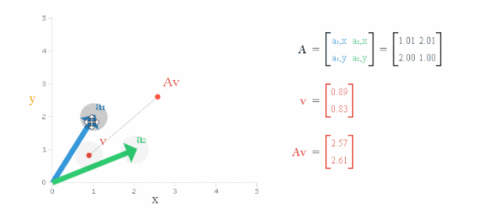
一个矩阵乘以一个向量,就相当于做了一个线性变换。但这个向量的方向往往会发生改变。
但若是存在一个矩阵A,让这个向量v在线性变换后,方向仍然保持不变,只是拉伸或者压缩一定倍数,即:Av=λv。
那么,这个向量v就是特征向量,λ就是特征值。
在现在的教科书里,已知特征向量求特征值比较容易,但是求矩阵的特征值又比求特征向量方便。
但三位物理学家在计算中微子振荡概率的时候发现:
特征向量和特征值的几何本质,其实就是空间矢量的旋转和缩放。而中微子的三个味(电子,μ子,τ子),不就相当于空间中的三个向量之间的变换吗?
中微子振荡是一种量子力学现象。实验发现,电子中微子、μ子中微子和τ子中微子这三种中微子之间是可以相互转化的,而这就是中微子振荡现象。
△图源:Quantamagazine
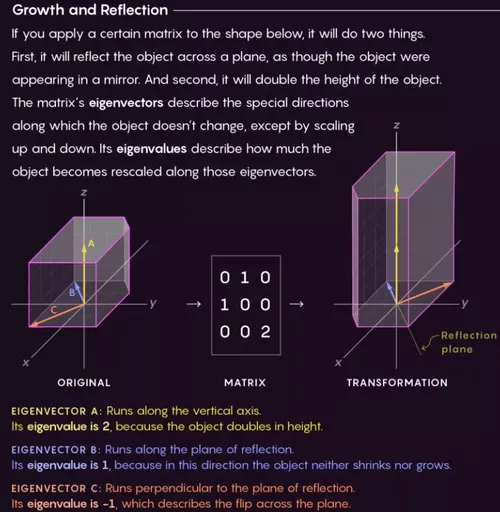
物理学家们意识到,特征向量和特征值之间,可能存在更普遍的规律。于是,新公式的面纱被揭开了。
通过删除原始矩阵的行和列,创建子矩阵。
子矩阵和原始矩阵的特征值组合在一起,就可以计算原始矩阵的特征向量。
简而言之,已知特征值,一个方程式就可以求得特征向量。
△图源:Quantamagazine
这个新公式有多牛?
数学天才、菲尔兹奖得主陶哲轩评价道:
新公式的非凡之处是,在任何情况下,你不需要知道矩阵中的任何元素,就可以计算出你想要的任何东西。
证明过程
在陶哲轩的回信中,他还附上了这一新公式的三种证明方法,并在之后和Peter Denton、Stephen Parke、张西宁三位物理学家一起发表了论文。
先定义A为一个n x n的厄米特矩阵,它具有特征向量λi(A)和赋范特征向量vi。
厄米特矩阵(Hermitian Matrix)能够将特征向量转化为实数,更适用于解决现实世界的问题。
特征向量中的每个元素标记为vi,j。
通过删除jth行和jth列,可以得到A的子矩阵Mj,大小为(n-1) x (n-1),它的特征值为λk(Mj)。
首先,通过证明可以得到一个柯西-比内(Cauchy-Binet)型公式。
引理1。让A的一个特征值为0,不失一般性的,可以让λn(A)=0。那么对于任意大小为n x (n-1)的矩阵B,我们可以得到:
接下来就可以进入新公式的推导了。
引理2。特征向量各元素的范数平方与其特征值、子矩阵特征值有关。
于是可以证明:令j=1且i=n。通过λn(A)In 转化(shift) A,使得λn(A)=0;这也同样转化了A和Mj中所有剩余的特征值,因此公式2就变为:
注意,公式3的右侧为det(M1)。
接下来,在B=(0,In-1)中应用引理1。我们发现公式1的左边为,公式1的右边为det(M1)。
证明:对于任意不是A的特征值的λ,
对于,j∈[1,n]有,
进一步简化,并取极限λ→λi(A),
公式7右边的对角元素提供了公式2的左半部分。通过共轭的定义,公式7左边的对角元素决定了λi(A)In-A的子矩阵。
应用引理2,必然的结论就是,如果特征向量中的一个元素消失,vi,j=0,那么矩阵A的特征向量方程将化为其子矩阵Mj的一个特征向量方程。
这一发现所带来的影响
简而言之,物理学家们的这一最新成果,将使人们可以仅使用特征值信息,计算出特征向量。
而在现在的教科书里,用特征向量求特征值比较容易,但是求矩阵的特征值又比求特征向量方便。
也就是说,这一成果揭示了基础数学新的事实。
更为重要的是,在现实世界中,无论是在数学、物理学还是工程学中,许许多多的问题都涉及到特征向量和特征值的计算。
比如计算中微子振荡概率。
比如在机器学习领域,数据降维,人脸识别,都涉及矩阵特征值/特征向量理论的实际应用。
俄亥俄州立大学的粒子物理学家John Beacom指出,这一理论应用前景广泛,甚至将打开新世界的大门。
物理学家和数学天才的合作
被三位物理学家邀请,并证明了新公式的数学家是公认的数学天才陶哲轩(Terence Tao)。
△陶哲轩
他7岁读高中,9岁上大学,13岁获得国际奥林匹克数学竞赛金牌,是IMO金银铜牌最年轻得主纪录的保持者。
24岁,他就成为UCLA数学系终身教授,31岁获得了有“数学界诺贝尔奖”之称的菲尔兹奖,成为第二位获此殊荣的华裔数学家。
而三位物理学家,一位是美国布鲁克黑文国家实验室的助理物理学家彼得·丹顿(Peter B.Denton)。2016年博士毕业于范德比尔特大学物理系。
另一位是新西兰物理学家斯蒂芬·帕克(Stephen J. Parke)。他是美国费米国家加速器实验室的杰出科学家和理论物理系主任,专注于中微子物理学和顶夸克物理学研究。
最后一位作者张西宁(Xining Zhang)同样是华人面孔,就读于芝加哥大学,从事理论粒子物理研究,是斯蒂芬·帕克的弟子。
共同学习,写下你的评论
评论加载中...
作者其他优质文章